§1.4 Calculus of One Variable

Keywords:: calculus
Permalink:: http://dlmf.nist.gov/1.4

§1.4(i) Monotonicity
§1.4(ii) Continuity
§1.4(iii) Derivatives
§1.4(iv) Indefinite Integrals
§1.4(v) Definite Integrals
§1.4(vi) Taylor’s Theorem for Real Variables
§1.4(vii) Maxima and Minima
§1.4(viii) Convex Functions

§1.4(i) Monotonicity

Keywords:: functions, monotonicity
Permalink:: http://dlmf.nist.gov/1.4.i

If $f(x_{1})\leq f(x_{2})$ for every pair $x_{1}$ , $x_{2}$ in an interval $I$ such that $x_{1}<x_{2}$ , then $f(x)$ is nondecreasing on $I$ . If the $\leq$ sign is replaced by $<$ , then $f(x)$ is increasing (also called strictly increasing) on $I$ . Similarly for nonincreasing and decreasing (strictly decreasing) functions. Each of the preceding four cases is classified as monotonic; sometimes strictly monotonic is used for the strictly increasing or strictly decreasing cases.

§1.4(ii) Continuity

Notes:: See Hardy (1952, Chapter 5) and Olver (1997b, p. 73).
Keywords:: continuous function, discontinuity, functions, limits of functions, piecewise continuous, simple discontinuity, singularity
Referenced by:: §1.17(i), §2.3(ii)
Permalink:: http://dlmf.nist.gov/1.4.ii

A function $f(x)$ is continuous on the right (or from above) at $x=c$ if

1.4.1 $f(c+)\equiv\lim _{{x\to c+}}f(x)=f(c),$

Referenced by:: §1.4(ii)
Permalink:: http://dlmf.nist.gov/1.4.E1
Encodings:: TeX, pMML, png

that is, for every arbitrarily small positive constant $\epsilon$ there exists $\delta$ ( $>0$ ) such that

1.4.2 $|f(c+\alpha)-f(c)|<\epsilon,$

Permalink:: http://dlmf.nist.gov/1.4.E2
Encodings:: TeX, pMML, png

for all $\alpha$ such that $0\leq\alpha<\delta$ . Similarly, it is continuous on the left (or from below) at $x=c$ if

1.4.3 $f(c-)\equiv\lim _{{x\to c-}}f(x)=f(c).$

Referenced by:: §1.4(ii)
Permalink:: http://dlmf.nist.gov/1.4.E3
Encodings:: TeX, pMML, png

And $f(x)$ is continuous at $c$ when both (1.4.1) and (1.4.3) apply.

If $f(x)$ is continuous at each point $c\in(a,b)$ , then $f(x)$ is continuous on the interval $(a,b)$ and we write $f\in\mathop{C\/}\nolimits(a,b)$ . If also $f(x)$ is continuous on the right at $x=a$ , and continuous on the left at $x=b$ , then $f(x)$ is continuous on the interval $[a,b]$ , and we write $f(x)\in\mathop{C\/}\nolimits[a,b]$ .

A removable singularity of $f(x)$ at $x=c$ occurs when $f(c+)=f(c-)$ but $f(c)$ is undefined. For example, $f(x)=(\mathop{\sin\/}\nolimits x)/x$ with $c=0$ .

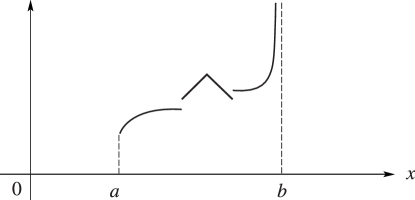
A simple discontinuity of $f(x)$ at $x=c$ occurs when $f(c+)$ and $f(c-)$ exist, but $f(c+)\not=f(c-)$ . If $f(x)$ is continuous on an interval $I$ save for a finite number of simple discontinuities, then $f(x)$ is piecewise (or sectionally) continuous on $I$ . For an example, see Figure 1.4.1

Figure 1.4.1: Piecewise continuous function on $[a,b)$ .

Symbols:: $[a,b)$ : half-closed interval
Referenced by:: §1.4(ii)
Permalink:: http://dlmf.nist.gov/1.4.F1
Encodings:: pdf, png

§1.4(iii) Derivatives

Notes:: See Hardy (1952, Chapter 6) or Rudin (1976, Chapter 5). For (1.4.13) see Riordan (1958, pp. 35–36) and Knuth (1968, p. 50).
Keywords:: derivatives
Referenced by:: §1.2(iii), §1.4(vii)
Permalink:: http://dlmf.nist.gov/1.4.iii

The derivative $f^{{\prime}}(x)$ of $f(x)$ is defined by

1.4.4 $f^{{\prime}}(x)=\frac{df}{dx}=\lim _{{h\to 0}}\frac{f(x+h)-f(x)}{h}.$

Defines:: $\frac{df}{dx}$ : derivative of $f$ with respect to $x$
Referenced by:: §1.8(ii)
Permalink:: http://dlmf.nist.gov/1.4.E4
Encodings:: TeX, pMML, png

When this limit exists $f$ is differentiable at $x$ .

1.4.5 $(f+g)^{{\prime}}(x)=f^{{\prime}}(x)+g^{{\prime}}(x),$

A&S Ref:: 3.3.2
Permalink:: http://dlmf.nist.gov/1.4.E5
Encodings:: TeX, pMML, png

1.4.6 $(fg)^{{\prime}}(x)=f^{{\prime}}(x)g(x)+f(x)g^{{\prime}}(x),$

A&S Ref:: 3.3.3
Permalink:: http://dlmf.nist.gov/1.4.E6
Encodings:: TeX, pMML, png

1.4.7 $\left(\frac{f}{g}\right)^{\prime}(x)=\frac{f^{{\prime}}(x)g(x)-f(x)g^{{\prime}}(x)}{(g(x))^{2}}.$

A&S Ref:: 3.3.4
Permalink:: http://dlmf.nist.gov/1.4.E7
Encodings:: TeX, pMML, png

¶ Higher Derivatives

Keywords:: differentiable functions, functions

1.4.8 $f^{{(2)}}(x)=\frac{{d}^{2}f}{{dx}^{2}}=\frac{d}{dx}\left(\frac{df}{dx}\right),$

Symbols:: $\frac{df}{dx}$ : derivative of $f$ with respect to $x$
Permalink:: http://dlmf.nist.gov/1.4.E8
Encodings:: TeX, pMML, png

1.4.9 $f^{{(n)}}=f^{{(n)}}(x)=\frac{d}{dx}f^{{(n-1)}}(x).$

Symbols:: $\frac{df}{dx}$ : derivative of $f$ with respect to $x$ and $n$ : nonnegative integer
Permalink:: http://dlmf.nist.gov/1.4.E9
Encodings:: TeX, pMML, png

If $f^{{(n)}}$ exists and is continuous on an interval $I$ , then we write $f\in\mathop{C^{{n}}\/}\nolimits(I)$ . When $n\geq 1$ , $f$ is continuously differentiable on $I$ . When $n$ is unbounded, $f$ is infinitely differentiable on $I$ and we write $f\in\mathop{C^{{\infty}}\/}\nolimits(I)$ .

¶ Chain Rule

Keywords:: chain rule, derivatives

For $h(x)=f(g(x))$ ,

1.4.10 $h^{{\prime}}(x)=f^{{\prime}}(g(x))g^{{\prime}}(x).$

A&S Ref:: 3.3.5
Permalink:: http://dlmf.nist.gov/1.4.E10
Encodings:: TeX, pMML, png

¶ Maxima and Minima

Keywords:: maximum, minimum

A necessary condition that a differentiable function $f(x)$ has a local maximum (minimum) at $x=c$ , that is, $f(x)\leq f(c)$ , ( $f(x)\geq f(c)$ ) in a neighborhood $c-\delta\leq x\leq c+\delta$ ( $\delta>0$ ) of $c$ , is $f^{{\prime}}(c)=0$ .

¶ Mean Value Theorem

Keywords:: derivatives, differentiable functions, mean value theorems

If $f(x)$ is continuous on $[a,b]$ and differentiable on $(a,b)$ , then there exists a point $c\in(a,b)$ such that

1.4.11 $f(b)-f(a)=(b-a)f^{{\prime}}(c).$

Permalink:: http://dlmf.nist.gov/1.4.E11
Encodings:: TeX, pMML, png

If $f^{{\prime}}(x)\geq 0$ ( $\leq 0$ ) ( $=0$ ) for all $x\in(a,b)$ , then $f$ is nondecreasing (nonincreasing) (constant) on $(a,b)$ .

¶ Leibniz’s Formula

Keywords:: Leibniz’s formula for derivatives, derivatives

1.4.12 $(fg)^{{(n)}}=f^{{(n)}}g+\binom{n}{1}f^{{(n-1)}}g^{{\prime}}+\dots+\binom{n}{k}f^{{(n-k)}}g^{{(k)}}+\dots+fg^{{(n)}}.$

Symbols:: $\binom{m}{n}$ : binomial coefficient, $k$ : integer and $n$ : nonnegative integer
A&S Ref:: 3.3.8
Permalink:: http://dlmf.nist.gov/1.4.E12
Encodings:: TeX, pMML, png

¶ Faà Di Bruno’s Formula

Keywords:: Faà di Bruno’s formula, derivatives

1.4.13 $\frac{{d}^{n}}{{dx}^{n}}f(g(x))=\sum\left(\frac{n!}{m_{1}!m_{2}!\cdots m_{n}!}\right)f^{{(k)}}(g(x))\*\left(\frac{g^{{\prime}}(x)}{1!}\right)^{{m_{1}}}\left(\frac{g^{{\prime\prime}}(x)}{2!}\right)^{{m_{2}}}\dots\left(\frac{g^{{(n)}}(x)}{n!}\right)^{{m_{n}}},$

Symbols:: $\frac{df}{dx}$ : derivative of $f$ with respect to $x$ , $!$ : $n!$ : factorial, $k$ : integer, $m$ : nonnegative integer and $n$ : nonnegative integer
Referenced by:: §1.4(iii)
Permalink:: http://dlmf.nist.gov/1.4.E13
Encodings:: TeX, pMML, png

where the sum is over all nonnegative integers $m_{1},m_{2},\dots,m_{n}$ that satisfy $m_{1}+2m_{2}+\dots+nm_{n}=n$ , and $k=m_{1}+m_{2}+\dots+m_{n}$ .

¶ L’Hôpital’s Rule

Keywords:: L’Hôpital’s rule for derivatives, derivatives

1.4.14 $\lim\limits _{{x\to a}}f(x)=\lim\limits _{{x\to a}}g(x)=0\;\;\mbox{(or $\infty$)},$

Permalink:: http://dlmf.nist.gov/1.4.E14
Encodings:: TeX, pMML, png

then

1.4.15 $\lim _{{x\to a}}\frac{f(x)}{g(x)}=\lim _{{x\to a}}\frac{f^{{\prime}}(x)}{g^{{\prime}}(x)},$

A&S Ref:: 3.4.1
Permalink:: http://dlmf.nist.gov/1.4.E15
Encodings:: TeX, pMML, png

when the last limit exists.

§1.4(iv) Indefinite Integrals

Notes:: See Hardy (1952, pp. 247–248, 258).
Defines:: $\int$ : integral and $dx$ : differential of $x$
Keywords:: integrals, integration
Permalink:: http://dlmf.nist.gov/1.4.iv

If $F^{{\prime}}(x)=f(x)$ , then $\int fdx=F(x)+C$ , where $C$ is a constant.

¶ Integration by Parts

Keywords:: integrals, integration

1.4.16 $\int fgdx=\left(\int fdx\right)g-\int\left(\int fdx\right)\frac{dg}{dx}dx.$

Symbols:: $\frac{df}{dx}$ : derivative of $f$ with respect to $x$ , $dx$ : differential of $x$ and $\int$ : integral
A&S Ref:: 3.3.13
Permalink:: http://dlmf.nist.gov/1.4.E16
Encodings:: TeX, pMML, png

1.4.17 $\int x^{n}dx=\begin{cases}\dfrac{x^{{n+1}}}{n+1}+C,&n\not=-1,\\ \mathop{\ln\/}\nolimits\left|x\right|+C,&n=-1.\end{cases}$

Symbols:: $dx$ : differential of $x$ , $\int$ : integral, $\mathop{\ln\/}\nolimits z$ : principal branch of logarithm function, $n$ : nonnegative integer and $C$ : constant
Permalink:: http://dlmf.nist.gov/1.4.E17
Encodings:: TeX, pMML, png

For the function $\mathop{\ln\/}\nolimits$ see §4.2(i).

See §§4.10, 4.26(ii), 4.26(iv), 4.40(ii), and 4.40(iv) for indefinite integrals involving the elementary functions.

For extensive tables of integrals, see Apelblat (1983), Bierens de Haan (1867), Gradshteyn and Ryzhik (2000), Gröbner and Hofreiter (1949, 1950), and Prudnikov et al. (1986a, b, 1990, 1992a, 1992b).

§1.4(v) Definite Integrals

Notes:: See Hardy (1952, Chapters 6, 7). For (1.4.31) integrate by parts. For (1.4.34) see Olver (1997b, p. 28).
Keywords:: integrals, integration
Referenced by:: ¶ ‣ §1.14(i), ¶ ‣ §1.14(ii), §1.9(iii), ¶ ‣ §10.22(ii), ¶ ‣ §10.23(iii), ¶ ‣ §18.17(viii), §19.2(ii), §2.3(i), §2.6(ii), §28.28(iii), §4.10(i), §9.10(vii), §9.12(vii)
Permalink:: http://dlmf.nist.gov/1.4.v

Suppose $f(x)$ is defined on $[a,b]$ . Let $a=x_{0}<x_{1}<\dots<x_{n}=b$ , and $\xi _{j}$ denote any point in $[x_{j},x_{{j+1}}]$ , $j=0,1,\dots,n-1$ . Then

1.4.18 $\int^{b}_{a}f(x)dx=\lim\sum^{{n-1}}_{{j=0}}f(\xi _{j})(x_{{j+1}}-x_{j})$

Symbols:: $dx$ : differential of $x$ , $\int$ : integral, $j$ : integer, $n$ : nonnegative integer and $\xi _{j}$ : point
Permalink:: http://dlmf.nist.gov/1.4.E18
Encodings:: TeX, pMML, png

as $\max(x_{{j+1}}-x_{j})\to 0$ . Continuity, or piecewise continuity, of $f(x)$ on $[a,b]$ is sufficient for the limit to exist.

1.4.19 $\int^{b}_{a}(cf(x)+dg(x))dx=c\int^{b}_{a}f(x)dx+d\int^{b}_{a}g(x)dx,$

Symbols:: $dx$ : differential of $x$ and $\int$ : integral
Permalink:: http://dlmf.nist.gov/1.4.E19
Encodings:: TeX, pMML, png

$c$ and $d$ constants.

1.4.20 $\int^{b}_{a}f(x)dx=-\int^{a}_{b}f(x)dx.$

Symbols:: $dx$ : differential of $x$ and $\int$ : integral
Permalink:: http://dlmf.nist.gov/1.4.E20
Encodings:: TeX, pMML, png

1.4.21 $\int^{b}_{a}f(x)dx=\int^{c}_{a}f(x)dx+\int^{b}_{c}f(x)dx.$

Symbols:: $dx$ : differential of $x$ and $\int$ : integral
Permalink:: http://dlmf.nist.gov/1.4.E21
Encodings:: TeX, pMML, png

¶ Infinite Integrals

Keywords:: convergence, integrals

1.4.22 $\int^{\infty}_{a}f(x)dx=\lim _{{b\to\infty}}\int^{b}_{a}f(x)dx.$

Symbols:: $dx$ : differential of $x$ and $\int$ : integral
Referenced by:: ¶ ‣ §1.4(v), ¶ ‣ §1.5(v)
Permalink:: http://dlmf.nist.gov/1.4.E22
Encodings:: TeX, pMML, png

Similarly for $\int^{a}_{{-\infty}}$ . Next, if $f(b)=\pm\infty$ , then

1.4.23 $\int^{b}_{a}f(x)dx=\lim _{{c\to b-}}\int^{c}_{a}f(x)dx.$

Symbols:: $dx$ : differential of $x$ and $\int$ : integral
Referenced by:: ¶ ‣ §1.4(v), ¶ ‣ §1.5(v)
Permalink:: http://dlmf.nist.gov/1.4.E23
Encodings:: TeX, pMML, png

Similarly when $f(a)=\pm\infty$ .

When the limits in (1.4.22) and (1.4.23) exist, the integrals are said to be convergent. If the limits exist with $f(x)$ replaced by $|f(x)|$ , then the integrals are absolutely convergent. Absolute convergence also implies convergence.

¶ Cauchy Principal Values

Keywords:: Cauchy principal values, integrals

Let $c\in(a,b)$ and assume that $\int _{a}^{{c-\epsilon}}f(x)dx$ and $\int _{{c+\epsilon}}^{b}f(x)dx$ exist when $0<\epsilon<\min(c-a,b-c)$ , but not necessarily when $\epsilon=0$ . Then we define

1.4.24 $\pvint^{b}_{a}f(x)dx=P\int^{b}_{a}f(x)dx=\lim _{{\epsilon\to 0+}}\left(\int^{{c-\epsilon}}_{a}f(x)dx+\int^{b}_{{c+\epsilon}}f(x)dx\right),$

Defines:: $\pvint _{a}^{b}$ : Cauchy principal value
Symbols:: $dx$ : differential of $x$ and $\int$ : integral
Permalink:: http://dlmf.nist.gov/1.4.E24
Encodings:: TeX, pMML, png

when this limit exists.

Similarly, assume that $\int _{{-b}}^{b}f(x)dx$ exists for all finite values of $b$ ( $>0$ ), but not necessarily when $b=\infty$ . Then we define

1.4.25 $\pvint^{\infty}_{{-\infty}}f(x)dx=P\int^{\infty}_{{-\infty}}f(x)dx=\lim _{{b\to\infty}}\int^{b}_{{-b}}f(x)dx,$

Symbols:: $dx$ : differential of $x$ , $\int$ : integral and $\pvint _{a}^{b}$ : Cauchy principal value
Referenced by:: ¶ ‣ §1.14(i)
Permalink:: http://dlmf.nist.gov/1.4.E25
Encodings:: TeX, pMML, png

when this limit exists.

¶ Fundamental Theorem of Calculus

Keywords:: differentiation, fundamental theorem of calculus, integrals

For $F^{{\prime}}(x)=f(x)$ with $f(x)$ continuous,

1.4.26 $\int^{b}_{a}f(x)dx=F(b)-F(a),$

Symbols:: $dx$ : differential of $x$ and $\int$ : integral
Permalink:: http://dlmf.nist.gov/1.4.E26
Encodings:: TeX, pMML, png

1.4.27 $\frac{d}{dx}\int^{x}_{a}f(t)dt=f(x).$

Symbols:: $\frac{df}{dx}$ : derivative of $f$ with respect to $x$ , $dx$ : differential of $x$ and $\int$ : integral
Permalink:: http://dlmf.nist.gov/1.4.E27
Encodings:: TeX, pMML, png

¶ Change of Variables

Keywords:: integrals

If $\phi^{{\prime}}(x)$ is continuous or piecewise continuous, then

1.4.28 $\int^{b}_{a}f(\phi(x))\phi^{{\prime}}(x)dx=\int^{{\phi(b)}}_{{\phi(a)}}f(t)dt.$

Symbols:: $dx$ : differential of $x$ , $\int$ : integral and $\phi(x)$ : function
Permalink:: http://dlmf.nist.gov/1.4.E28
Encodings:: TeX, pMML, png

¶ First Mean Value Theorem

Keywords:: integrals, mean value theorems

For $f(x)$ continuous and $\phi(x)\geq 0$ and integrable on $[a,b]$ , there exists $c\in[a,b]$ , such that

1.4.29 $\int^{b}_{a}f(x)\phi(x)dx=f(c)\int^{b}_{a}\phi(x)dx.$

Symbols:: $dx$ : differential of $x$ , $\int$ : integral and $\phi(x)$ : function
Permalink:: http://dlmf.nist.gov/1.4.E29
Encodings:: TeX, pMML, png

¶ Second Mean Value Theorem

Keywords:: integrals, mean value theorems

For $f(x)$ monotonic and $\phi(x)$ integrable on $[a,b]$ , there exists $c\in[a,b]$ , such that

1.4.30 $\int^{b}_{a}f(x)\phi(x)dx=f(a)\int^{c}_{a}\phi(x)dx+f(b)\int^{b}_{c}\phi(x)dx.$

Symbols:: $dx$ : differential of $x$ , $\int$ : integral and $\phi(x)$ : function
Permalink:: http://dlmf.nist.gov/1.4.E30
Encodings:: TeX, pMML, png

¶ Repeated Integrals

Keywords:: integrals

If $f(x)$ is continuous or piecewise continuous on $[a,b]$ , then

1.4.31 $\int _{a}^{b}dx_{n}\int _{a}^{{x_{n}}}dx_{{n-1}}\cdots\int _{a}^{{x_{2}}}dx_{1}\int _{a}^{{x_{1}}}f(x)dx=\frac{1}{n!}\int _{a}^{b}(b-x)^{n}f(x)dx.$

Symbols:: $dx$ : differential of $x$ , $!$ : $n!$ : factorial, $\int$ : integral and $n$ : nonnegative integer
Referenced by:: §1.15(vi), §1.4(v)
Permalink:: http://dlmf.nist.gov/1.4.E31
Encodings:: TeX, pMML, png

¶ Square-Integrable Functions

Keywords:: integrals, square-integrable function

A function $f(x)$ is square-integrable if

1.4.32 $\| f\|^{2}_{2}\equiv\int^{b}_{a}|f(x)|^{2}dx<\infty.$

Symbols:: $dx$ : differential of $x$ and $\int$ : integral
Permalink:: http://dlmf.nist.gov/1.4.E32
Encodings:: TeX, pMML, png

¶ Functions of Bounded Variation

Keywords:: bounded variation, closure, functions, interval, variation of real or complex functions

With $a<b$ , the total variation of $f(x)$ on a finite or infinite interval $(a,b)$ is

1.4.33 $\mathop{\mathcal{V}_{{a,b}}\/}\nolimits\!\left(f\right)=\sup\sum^{n}_{{j=1}}|f(x_{j})-f(x_{{j-1}})|,$

Defines:: $\mathop{\mathcal{V}_{{a,b}}\/}\nolimits\!\left(f\right)$ : total variation
Symbols:: $\sup$ : least upper bound (supremum), $j$ : integer and $n$ : nonnegative integer
Permalink:: http://dlmf.nist.gov/1.4.E33
Encodings:: TeX, pMML, png

where the supremum is over all sets of points $x_{0}<x_{1}<\dots<x_{n}$ in the closure of $(a,b)$ , that is, $(a,b)$ with $a,b$ added when they are finite. If $\mathop{\mathcal{V}_{{a,b}}\/}\nolimits\!\left(f\right)<\infty$ , then $f(x)$ is of bounded variation on $(a,b)$ . In this case, $g(x)=\mathop{\mathcal{V}_{{a,x}}\/}\nolimits\!\left(f\right)$ and $h(x)=\mathop{\mathcal{V}_{{a,x}}\/}\nolimits\!\left(f\right)-f(x)$ are nondecreasing bounded functions and $f(x)=g(x)-h(x)$ .

If $f(x)$ is continuous on the closure of $(a,b)$ and $f^{{\prime}}(x)$ is continuous on $(a,b)$ , then

1.4.34 $\mathop{\mathcal{V}_{{a,b}}\/}\nolimits\!\left(f\right)=\int^{b}_{a}|f^{{\prime}}(x)dx|,$

Symbols:: $dx$ : differential of $x$ , $\int$ : integral and $\mathop{\mathcal{V}_{{a,b}}\/}\nolimits\!\left(f\right)$ : total variation
Referenced by:: ¶ ‣ §1.4(v), §1.4(v)
Permalink:: http://dlmf.nist.gov/1.4.E34
Encodings:: TeX, pMML, png

whenever this integral exists.

Lastly, whether or not the real numbers $a$ and $b$ satisfy $a<b$ , and whether or not they are finite, we define $\mathop{\mathcal{V}_{{a,b}}\/}\nolimits\!\left(f\right)$ by (1.4.34) whenever this integral exists. This definition also applies when $f(x)$ is a complex function of the real variable $x$ . For further information on total variation see Olver (1997b, pp. 27–29).

§1.4(vi) Taylor’s Theorem for Real Variables

Notes:: See Hardy (1952, pp. 285–292, 327–328).
Keywords:: Taylor’s theorem
Referenced by:: §25.11(iv)
Permalink:: http://dlmf.nist.gov/1.4.vi

If $f(x)\in\mathop{C^{{n+1}}\/}\nolimits[a,b]$ , then

1.4.35 $f(x)=\sum^{n}_{{k=0}}\frac{f^{{(k)}}(a)}{k!}(x-a)^{k}+R_{n},$

Symbols:: $!$ : $n!$ : factorial, $k$ : integer, $n$ : nonnegative integer and $R_{n}$ : remainder
A&S Ref:: 3.6.4
Permalink:: http://dlmf.nist.gov/1.4.E35
Encodings:: TeX, pMML, png

1.4.36 $R_{n}=\frac{f^{{(n+1)}}(c)}{(n+1)!}(x-a)^{{n+1}},$ $a<c<x$ ,

Symbols:: $!$ : $n!$ : factorial, $n$ : nonnegative integer and $R_{n}$ : remainder
A&S Ref:: 3.6.5
Permalink:: http://dlmf.nist.gov/1.4.E36
Encodings:: TeX, pMML, png

and

1.4.37 $R_{n}=\frac{1}{n!}\int^{x}_{a}(x-t)^{n}f^{{(n+1)}}(t)dt.$

Symbols:: $dx$ : differential of $x$ , $!$ : $n!$ : factorial, $\int$ : integral, $n$ : nonnegative integer and $R_{n}$ : remainder
A&S Ref:: 3.6.3
Permalink:: http://dlmf.nist.gov/1.4.E37
Encodings:: TeX, pMML, png

§1.4(vii) Maxima and Minima

Notes:: See Hardy (1952, pp. 234–235).
Keywords:: maximum, minimum
Permalink:: http://dlmf.nist.gov/1.4.vii

If $f(x)$ is twice-differentiable, and if also $f^{{\prime}}(x_{0})=0$ and $f^{{\prime\prime}}(x_{0})<0$ ( $>0$ ), then $x=x_{0}$ is a local maximum (minimum) (§1.4(iii)) of $f(x)$ . The overall maximum (minimum) of $f(x)$ on $[a,b]$ will either be at a local maximum (minimum) or at one of the end points $a$ or $b$ .

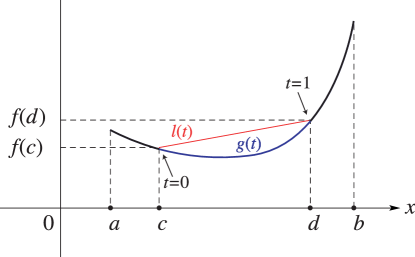
§1.4(viii) Convex Functions

Notes:: See Hardy et al. (1967, pp. 70–77).
Keywords:: calculus, convex functions, functions
Referenced by:: §1.7(iv), §5.5(iv)
Permalink:: http://dlmf.nist.gov/1.4.viii

A function $f(x)$ is convex on $(a,b)$ if

1.4.38 $f((1-t)c+td)\leq(1-t)f(c)+tf(d)$

Permalink:: http://dlmf.nist.gov/1.4.E38
Encodings:: TeX, pMML, png

for any $c,d\in(a,b)$ , and $t\in[0,1]$ . See Figure 1.4.2. A similar definition applies to closed intervals $[a,b]$ .

If $f(x)$ is twice differentiable, then $f(x)$ is convex iff $f^{{\prime\prime}}(x)\geq 0$ on $(a,b)$ . A continuously differentiable function is convex iff the curve does not lie below its tangent at any point.

Figure 1.4.2: Convex function $f(x)$ . $g(t)=f((1-t)c+td)$ , $l(t)=(1-t)f(c)+tf(d)$ , $c,d\in(a,b)$ , $0\leq t\leq 1$ .

Symbols:: $\in$ : element of and $(a,b)$ : open interval
Referenced by:: §1.4(viii)
Permalink:: http://dlmf.nist.gov/1.4.F2
Encodings:: pdf, png