calculus

SearchAdvancedHelp

(0.000 seconds)

1—10 of 17 matching pages

1: David M. Bressoud

… ► 227, in 1980, Factorization and Primality Testing, published by Springer-Verlag in 1989, Second Year Calculus from Celestial Mechanics to Special Relativity, published by Springer-Verlag in 1992, A Radical Approach to Real Analysis, published by the Mathematical Association of America in 1994, with a second edition in 2007, Proofs and Confirmations: The Story of the Alternating Sign Matrix Conjecture, published by the Mathematical Association of America and Cambridge University Press in 1999, A Course in Computational Number Theory (with S. …

2: Tom M. Apostol

… ►He was internationally known for his textbooks on calculus, analysis, and analytic number theory, which have been translated into five languages, and for creating Project MATHEMATICS!, a series of video programs that bring mathematics to life with computer animation, live action, music, and special effects. …

3: 24.17 Mathematical Applications

… ►

Calculus of Finite Differences

…

4: 1.4 Calculus of One Variable

§1.4 Calculus of One Variable

… ►

Fundamental Theorem of Calculus

… ►

►►

Figure 1.4.2: Convex function $f(x)$. … Magnify

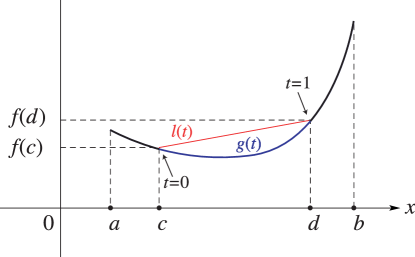5: Bibliography J

… ►

Calculus of Finite Differences. Hungarian Agent Eggenberger Book-Shop, Budapest.

ⓘ

Notes:

Third edition published in 1965 by Chelsea Publishing Co., New York, and American Mathematical Society, AMS Chelsea Book Series, Providence, RI

External Links:

MathReview (W. E. Milne), ZentralBlatt

Referenced by:

§26.1, §26.1, §26.8(vii), §5.16, Notations S.

Encodings:

BibTeX

►

Calculus of Finite Differences. 3rd edition, AMS Chelsea, Providence, RI.

ⓘ

External Links:

MathReview, ZentralBlatt

Referenced by:

§24.17(i), §24.6.

Encodings:

BibTeX

…

6: 17.2 Calculus

§17.2 Calculus

►

§17.2(i) $q$-Calculus

… ►

7: Bibliography R

… ►

The umbral calculus. Pure and Applied Mathematics, Vol. 111, Academic Press, Inc. [Harcourt Brace Jovanovich, Publishers], New York.

ⓘ

External Links:

ISBN 0-12-594380-6, MathReview (R. Askey)

Referenced by:

§18.2(xii).

Encodings:

BibTeX

… ►

On the foundations of combinatorial theory. VIII. Finite operator calculus. J. Math. Anal. Appl. 42, pp. 684–760.

ⓘ

External Links:

ISSN 0022-247X, Document, Link, MathReview (P. Saphar), ZentralBlatt

Referenced by:

§18.2(xii).

Encodings:

BibTeX

…

8: 1.5 Calculus of Two or More Variables

§1.5 Calculus of Two or More Variables

… ►

9: 24.4 Basic Properties

… ►

24.4.39 $$E_n\left(x+h\right)={(E(x)+h)}^n.$$

ⓘ

Symbols:

$E_n\left(x\right)$: Euler polynomials, $n$: integer and $x$: real or complex

A&S Ref:

23.1.26

Permalink:

http://dlmf.nist.gov/24.4.E39

Encodings:

pMML, png, TeX

See also:

Annotations for §24.4(viii), §24.4 and Ch.24

►For these results and also connections with the umbral calculus see Gessel (2003). …

10: Bibliography E

… ►

A Treatise on the Integral Calculus. Vol. 1-2, Chelsea Publishing Co., New York.

ⓘ

Notes:

Originally published by Macmillan, 1921-1930.

External Links:

ZentralBlatt

Referenced by:

§19.11(i), §19.4(ii).

Encodings:

BibTeX

…