§3.5 Quadrature

Keywords:: integration, quadrature
Referenced by:: §14.32, §19.36(iv), §29.20(i), §5.21
Permalink:: http://dlmf.nist.gov/3.5

§3.5(i) Trapezoidal Rules
§3.5(ii) Simpson’s Rule
§3.5(iii) Romberg Integration
§3.5(iv) Interpolatory Quadrature Rules
§3.5(v) Gauss Quadrature
§3.5(vi) Eigenvalue/Eigenvector Characterization of Gauss Quadrature Formulas
§3.5(vii) Oscillatory Integrals
§3.5(viii) Complex Gauss Quadrature
§3.5(ix) Other Contour Integrals
§3.5(x) Cubature Formulas

§3.5(i) Trapezoidal Rules

Notes:: See Davis and Rabinowitz (1984, pp. 54 and 137).
Keywords:: quadrature
Referenced by:: ¶ ‣ §3.4(ii), ¶ ‣ §3.5(ix), §9.17(iii)
Permalink:: http://dlmf.nist.gov/3.5.i

The elementary trapezoidal rule is given by

3.5.1 $\int _{a}^{b}f(x)dx=\tfrac{1}{2}h(f(a)+f(b))-\tfrac{1}{12}h^{3}f^{{\prime\prime}}(\xi),$

Symbols:: $dx$ : differential of $x$ and $\int$ : integral
A&S Ref:: 25.4.1 (second relation only)
Permalink:: http://dlmf.nist.gov/3.5.E1
Encodings:: TeX, pMML, png

where $h=b-a$ , $f\in\mathop{C^{{2}}\/}\nolimits[a,b]$ , and $a<\xi<b$ .

The composite trapezoidal rule is

3.5.2 $\displaystyle\int _{a}^{b}f(x)dx=h(\tfrac{1}{2}f_{0}+f_{1}+\dots+f_{{n-1}}+\tfrac{1}{2}f_{n})+E_{n}(f),$

Symbols:: $dx$ : differential of $x$ , $\int$ : integral and $E_{n}(f)$ : error term
A&S Ref:: 25.4.2 (in slightly different form)
Referenced by:: §3.4(ii), ¶ ‣ §3.5(ix), §3.5(iii)
Permalink:: http://dlmf.nist.gov/3.5.E2
Encodings:: TeX, pMML, png

where $h=(b-a)/n$ , $x_{k}=a+kh$ , $f_{k}=f(x_{k})$ , $k=0,1,\dots,n$ , and

3.5.3 $E_{n}(f)=-\frac{b-a}{12}h^{2}f^{{\prime\prime}}(\xi),$ $a<\xi<b$ .

Symbols:: $E_{n}(f)$ : error term
A&S Ref:: 25.4.2 (in slightly different form)
Permalink:: http://dlmf.nist.gov/3.5.E3
Encodings:: TeX, pMML, png

If in addition $f$ is periodic, $f\in\mathop{C^{{k}}\/}\nolimits(\Real)$ , and the integral is taken over a period, then

3.5.4 $E_{n}(f)=\mathop{O\/}\nolimits\!\left(h^{k}\right),$ $h\to 0$ .

Symbols:: $\mathop{O\/}\nolimits\!\left(x\right)$ : order not exceeding and $E_{n}(f)$ : error term
A&S Ref:: 25.4.3 (in slightly different form)
Referenced by:: §3.5(i)
Permalink:: http://dlmf.nist.gov/3.5.E4
Encodings:: TeX, pMML, png

In particular, when $k=\infty$ the error term is an exponentially-small function of $1/h$ , and in these circumstances the composite trapezoidal rule is exceptionally efficient. For an example see §3.5(ix).

Similar results hold for the trapezoidal rule in the form

3.5.5 $\int _{{-\infty}}^{\infty}f(t)dt=h\sum _{{k=-\infty}}^{\infty}f(kh)+E_{h}(f),$

Symbols:: $dx$ : differential of $x$ , $\int$ : integral and $E_{n}(f)$ : error term
Referenced by:: §3.5(i)
Permalink:: http://dlmf.nist.gov/3.5.E5
Encodings:: TeX, pMML, png

with a function $f$ that is analytic in a strip containing $\Real$ . For further information and examples, see Goodwin (1949b). In Stenger (1993, Chapter 3) the rule (3.5.5) is considered in the framework of Sinc approximations (§3.3(vi)). See also Poisson’s summation formula (§1.8(iv)).

If $k$ in (3.5.4) is not arbitrarily large, and if odd-order derivatives of $f$ are known at the end points $a$ and $b$ , then the composite trapezoidal rule can be improved by means of the Euler–Maclaurin formula (§2.10(i)). See Davis and Rabinowitz (1984, pp. 134–142) and Temme (1996b, p. 25).

§3.5(ii) Simpson’s Rule

Notes:: See Davis and Rabinowitz (1984, pp. 57–58).
Keywords:: quadrature
Permalink:: http://dlmf.nist.gov/3.5.ii

Let $h=\frac{1}{2}(b-a)$ and $f\in\mathop{C^{{4}}\/}\nolimits[a,b]$ . Then the elementary Simpson’s rule is

3.5.6 $\int _{a}^{b}f(x)dx=\tfrac{1}{3}h(f(a)+4f(\tfrac{1}{2}(a+b))+f(b))-\tfrac{1}{90}h^{5}f^{{(4)}}(\xi),$

Symbols:: $dx$ : differential of $x$ and $\int$ : integral
A&S Ref:: 25.4.5 (second relation only)
Permalink:: http://dlmf.nist.gov/3.5.E6
Encodings:: TeX, pMML, png

where $a<\xi<b$ .

Now let $h=(b-a)/n$ , $x_{k}=a+kh$ , and $f_{k}=f(x_{k})$ , $k=0,1,\dots,n$ . Then the composite Simpson’s rule is

3.5.7 $\int _{a}^{b}f(x)dx=\tfrac{1}{3}h(f_{0}+4f_{1}+2f_{2}+4f_{3}+2f_{4}+\cdots+4f_{{n-1}}+f_{n})+E_{n}(f),$

Symbols:: $dx$ : differential of $x$ , $\int$ : integral and $E_{n}(f)$ : error term
A&S Ref:: 25.4.6 (in slightly different form)
Permalink:: http://dlmf.nist.gov/3.5.E7
Encodings:: TeX, pMML, png

where $n$ is even and

3.5.8 $E_{n}(f)=-\frac{b-a}{180}h^{4}f^{{(4)}}(\xi),$ $a<\xi<b$ .

Symbols:: $E_{n}(f)$ : error term
A&S Ref:: 25.4.6 (in slightly different form)
Permalink:: http://dlmf.nist.gov/3.5.E8
Encodings:: TeX, pMML, png

Simpson’s rule can be regarded as a combination of two trapezoidal rules, one with step size $h$ and one with step size $h/2$ to refine the error term.

§3.5(iii) Romberg Integration

Notes:: See Davis and Rabinowitz (1984, pp. 434–436) and Bauer et al. (1963).
Keywords:: quadrature
Permalink:: http://dlmf.nist.gov/3.5.iii

Further refinements are achieved by Romberg integration. If $f\in\mathop{C^{{2m+2}}\/}\nolimits[a,b]$ , then the remainder $E_{n}(f)$ in (3.5.2) can be expanded in the form

3.5.9 $E_{n}(f)=c_{1}h^{2}+c_{2}h^{4}+\dots+c_{m}h^{{2m}}+\mathop{O\/}\nolimits\!\left(h^{{2m+2}}\right),$

Symbols:: $\mathop{O\/}\nolimits\!\left(x\right)$ : order not exceeding, $E_{n}(f)$ : error term and $c_{m}$ : coefficients
Referenced by:: §3.5(iii)
Permalink:: http://dlmf.nist.gov/3.5.E9
Encodings:: TeX, pMML, png

where $h=(b-a)/n$ . As in Simpson’s rule, by combining the rule for $h$ with that for $h/2$ , the first error term $c_{1}h^{2}$ in (3.5.9) can be eliminated. With the Romberg scheme successive terms $c_{1}h^{2},c_{2}h^{4},\dots$ , in (3.5.9) are eliminated, according to the formula

3.5.10 $G_{k}(\tfrac{1}{2}h)=G_{{k-1}}(\tfrac{1}{2}h)+\frac{G_{{k-1}}(\frac{1}{2}h)-G_{{k-1}}(h)}{4^{k}-1},$ $k\geq 1$ ,

Symbols:: $G_{k}(h)$ : Romberg scheme
Referenced by:: ¶ ‣ §3.5(iii)
Permalink:: http://dlmf.nist.gov/3.5.E10
Encodings:: TeX, pMML, png

beginning with

3.5.11 $G_{0}(h)=h(\tfrac{1}{2}f_{0}+f_{1}+\dots+f_{{n-1}}+\tfrac{1}{2}f_{n}),$

Symbols:: $G_{k}(h)$ : Romberg scheme
Permalink:: http://dlmf.nist.gov/3.5.E11
Encodings:: TeX, pMML, png

although we may also start with the elementary rule with $G_{0}(h)=\frac{1}{2}h(f(a)+f(b))$ and $h=b-a$ . To generate $G_{k}(h)$ the quantities $G_{0}(h),G_{0}(h/2),\dots,G_{0}(h/2^{k})$ are needed. These can be found by means of the recursion

3.5.12 $G_{0}(\tfrac{1}{2}h)=\tfrac{1}{2}G_{0}(h)+\tfrac{1}{2}h\sum _{{k=0}}^{{n-1}}f\left(x_{0}+(k+\tfrac{1}{2})h\right),$

Symbols:: $G_{k}(h)$ : Romberg scheme
Permalink:: http://dlmf.nist.gov/3.5.E12
Encodings:: TeX, pMML, png

which depends on function values computed previously.

If $f\in\mathop{C^{{2k+2}}\/}\nolimits(a,b)$ , then for $j,k=0,1,\dots$ ,

3.5.13 $\int _{a}^{b}f(x)dx-G_{k}\left(\frac{b-a}{2^{j}}\right)=-\frac{(b-a)^{{2k+3}}}{2^{{k(k+1)}}}\frac{4^{{-j(k+1)}}}{(2k+2)!}\left|\mathop{B_{{2k+2}}\/}\nolimits\right|f^{{(2k+2)}}(\xi),$

Symbols:: $\mathop{B_{{n}}\/}\nolimits\!\left(x\right)$ : Bernoulli polynomials, $dx$ : differential of $x$ , $!$ : $n!$ : factorial, $\int$ : integral and $G_{k}(h)$ : Romberg scheme
Referenced by:: ¶ ‣ §3.5(iii)
Permalink:: http://dlmf.nist.gov/3.5.E13
Encodings:: TeX, pMML, png

for some $\xi\in(a,b)$ . For the Bernoulli numbers $\mathop{B_{{m}}\/}\nolimits$ see §24.2(i).

When $f\in\mathop{C^{{\infty}}\/}\nolimits$ , the Romberg method affords a means of obtaining high accuracy in many cases with a relatively simple adaptive algorithm. However, as illustrated by the next example, other methods may be more efficient.

¶ Example

With $\mathop{J_{{0}}\/}\nolimits\!\left(t\right)$ denoting the Bessel function (§10.2(ii)) the integral

3.5.14 $\int _{0}^{\infty}e^{{-pt}}\mathop{J_{{0}}\/}\nolimits\!\left(t\right)dt=\frac{1}{\sqrt{p^{2}+1}}$

Symbols:: $\mathop{J_{{\nu}}\/}\nolimits\!\left(z\right)$ : Bessel function of the first kind, $dx$ : differential of $x$ , $e$ : base of exponential function and $\int$ : integral
Permalink:: http://dlmf.nist.gov/3.5.E14
Encodings:: TeX, pMML, png

is computed with $p=1$ on the interval $[0,30]$ . Using (3.5.10) with $h=30/4=7.5$ we obtain $G_{7}(h)$ with 14 correct digits. About $2^{9}=512$ function evaluations are needed. (With the 20-point Gauss–Laguerre formula (§3.5(v)) the same precision can be achieved with 15 function evaluations.) With $j=2$ and $k=7$ , the coefficient of the derivative $f^{{(16)}}(\xi)$ in (3.5.13) is found to be $(0.14\dots)\times 10^{{-13}}$ .

See Davis and Rabinowitz (1984, pp. 440–441) for modifications of the Romberg method when the function $f$ is singular.

§3.5(iv) Interpolatory Quadrature Rules

Notes:: For (3.5.18)–(3.5.19) see Waldvogel (2006).
Keywords:: Clenshaw–Curtis quadrature formula, Gauss quadrature, error term, nodes, quadrature, weight functions
Referenced by:: §3.5(vii), Version 1.0.3 (Aug 29, 2011)
Permalink:: http://dlmf.nist.gov/3.5.iv
Addition (effective with 1.0.3):: The reference to Trefethen (2011) was added at the end of this subsection.
Reported 2011-08-21

An interpolatory quadrature rule

3.5.15 $\int _{a}^{b}f(x)w(x)dx=\sum _{{k=1}}^{n}w_{k}f(x_{k})+E_{n}(f),$

Symbols:: $dx$ : differential of $x$ , $\int$ : integral, $E_{n}(f)$ : error term, $w$ : weight and $w_{k}$ : weights
Referenced by:: §3.5(v)
Permalink:: http://dlmf.nist.gov/3.5.E15
Encodings:: TeX, pMML, png

with weight function $w(x)$ , is one for which $E_{n}(f)=0$ whenever $f$ is a polynomial of degree $\leq n-1$ . The nodes $x_{1},x_{2},\dots,x_{n}$ are prescribed, and the weights $w_{k}$ and error term $E_{n}(f)$ are found by integrating the product of the Lagrange interpolation polynomial of degree $n-1$ and $w(x)$ .

If the extreme members of the set of nodes $x_{1},x_{2},\dots,x_{n}$ are the endpoints $a$ and $b$ , then the quadrature rule is said to be closed. Or if the set $x_{1},x_{2},\dots,x_{n}$ lies in the open interval $(a,b)$ , then the quadrature rule is said to be open.

Rules of closed type include the Newton–Cotes formulas such as the trapezoidal rules and Simpson’s rule. Examples of open rules are the Gauss formulas (§3.5(v)), the midpoint rule, and Fejér’s quadrature rule. For the latter $a=-1$ , $b=1$ , and the nodes $x_{k}$ are the extrema of the Chebyshev polynomial $\mathop{T_{{n}}\/}\nolimits\!\left(x\right)$ (§3.11(ii) and §18.3). If we add −1 and 1 to this set of $x_{k}$ , then the resulting closed formula is the frequently-used Clenshaw–Curtis formula, whose weights are positive and given by

3.5.16 $w_{k}=\frac{g_{k}}{n}\left(1-\sum _{{j=1}}^{{\left\lfloor n/2\right\rfloor}}\frac{b_{j}}{4j^{2}-1}\mathop{\cos\/}\nolimits\!\left(2jk\pi/n\right)\right),$

Symbols:: $\mathop{\cos\/}\nolimits z$ : cosine function, $\left\lfloor x\right\rfloor$ : floor of $x$ , $w_{k}$ : weights, $g_{k}$ : coefficient and $b_{k}$ : coefficient
Permalink:: http://dlmf.nist.gov/3.5.E16
Encodings:: TeX, pMML, png

where $x_{k}=\mathop{\cos\/}\nolimits\!\left(k\pi/n\right),k=0,1,\ldots,n$ , and

3.5.17 $g_{k}=\begin{cases}1,&\text{$k=0,n$},\\ 2,&\text{otherwise},\end{cases}\quad b_{j}=\begin{cases}1,&\text{$j=\frac{1}{2}n$},\\ 2,&\text{otherwise}.\end{cases}$

Symbols:: $g_{k}$ : coefficient and $b_{k}$ : coefficient
Permalink:: http://dlmf.nist.gov/3.5.E17
Encodings:: TeX, pMML, png

For further information, see Mason and Handscomb (2003, Chapter 8), Davis and Rabinowitz (1984, pp. 74–92), and Clenshaw and Curtis (1960).

For detailed comparisons of the Clenshaw–Curtis formula with Gauss quadrature (§3.5(v)), see Trefethen (2008, 2011).

§3.5(v) Gauss Quadrature

Notes:: In this subsection all numerical values of the nodes $x_{k}$ and corresponding weights $w_{k}$ that appear in the tables in the text and on the Web site can be computed, for example, by means of the quadruple-precision analogs of the softwares recur and gauss given in Gautschi (1994), or in the case of the tables for the logarithmic weight function with recur replaced by cheb, also provided in Gautschi (1994). The three softwares can be used for other values of $n$ , and other values of the parameters $\alpha$ and $\beta$ that appear in some of the weight functions.
Keywords:: Christoffel coefficients (or numbers), Gauss–Christoffel quadrature, Gauss quadrature, nodes, quadrature, weight functions
Referenced by:: §10.74(iii), ¶ ‣ §18.38(i), §18.41(ii), ¶ ‣ §3.5(iii), §3.5(iv), §3.5(iv), §6.18(i), §9.17(iii)
Permalink:: http://dlmf.nist.gov/3.5.v

Let $\{ p_{n}\}$ denote the set of monic polynomials $p_{n}$ of degree $n$ (coefficient of $x^{n}$ equal to 1) that are orthogonal with respect to a positive weight function $w$ on a finite or infinite interval $(a,b)$ ; compare §18.2(i). In Gauss quadrature (also known as Gauss–Christoffel quadrature) we use (3.5.15) with nodes $x_{k}$ the zeros of $p_{n}$ , and weights $w_{k}$ given by

3.5.18 $w_{k}=\int _{a}^{b}\frac{p_{n}(x)}{(x-x_{k})p^{{\mspace{1.0mu}\prime}}_{n}(x_{k})}\, w(x)dx.$

Symbols:: $dx$ : differential of $x$ , $\int$ : integral, $w$ : weight, $w_{k}$ : weights and $p_{n}$ : set of monic polynomials
Referenced by:: §3.5(iv)
Permalink:: http://dlmf.nist.gov/3.5.E18
Encodings:: TeX, pMML, png

The $w_{k}$ are also known as Christoffel coefficients or Christoffel numbers and they are all positive. The remainder is given by

3.5.19 $E_{n}(f)=\gamma _{n}f^{{(2n)}}(\xi)/(2n)!,$

Symbols:: $!$ : $n!$ : factorial, $\gamma _{n}$ : coefficients and $E_{n}(f)$ : error term
Referenced by:: §3.5(iv)
Permalink:: http://dlmf.nist.gov/3.5.E19
Encodings:: TeX, pMML, png

where

3.5.20 $\gamma _{n}=\int _{a}^{b}p_{n}^{2}(x)w(x)dx,$

Symbols:: $dx$ : differential of $x$ , $\int$ : integral, $\gamma _{n}$ : coefficients, $w$ : weight and $p_{n}$ : set of monic polynomials
A&S Ref:: 25.4.29 (for general weight function)
Referenced by:: §3.5(vi)
Permalink:: http://dlmf.nist.gov/3.5.E20
Encodings:: TeX, pMML, png

and $\xi$ is some point in $(a,b)$ . As a consequence, the rule is exact for polynomials of degree $\leq 2n-1$ .

In practical applications the weight function $w(x)$ is chosen to simulate the asymptotic behavior of the integrand as the endpoints are approached. For $\mathop{C^{{\infty}}\/}\nolimits$ functions Gauss quadrature can be very efficient. In adaptive algorithms the evaluation of the nodes and weights may cause difficulties, unless exact values are known.

For the derivation of Gauss quadrature formulas see Gautschi (2004, pp. 22–32), Gil et al. (2007a, §5.3), and Davis and Rabinowitz (1984, §§2.7 and 3.6). Stroud and Secrest (1966) includes computational methods and extensive tables. For further extensions, applications, and computation of orthogonal polynomials and Gauss-type formulas, see Gautschi (1994, 1996, 2004). For effective testing of Gaussian quadrature rules see Gautschi (1983).

For the classical orthogonal polynomials related to the following Gauss rules, see §18.3. The given quantities $\gamma _{n}$ follow from (18.2.5), (18.2.7), Table 18.3.1, and the relation $\gamma _{n}=\ifrac{h_{n}}{k_{n}^{2}}$ .

¶ Gauss–Legendre Formula

Keywords:: Gauss quadrature, Legendre polynomials, monic polynomial, nodes, polynomials, weight functions

3.5.21

$[a,b]=[-1,1],$

$w(x)=1,$

$\gamma _{n}=\frac{2^{{2n+1}}}{2n+1}\,\frac{(n!)^{4}}{((2n)!)^{2}}\,.$

Symbols:: $[a,b]$ : closed interval, $!$ : $n!$ : factorial, $\gamma _{n}$ : coefficients and $w$ : weight
A&S Ref:: 25.4.29
Permalink:: http://dlmf.nist.gov/3.5.E21
Encodings:: TeX, TeX, TeX, pMML, pMML, pMML, png, png, png

The nodes $x_{k}$ and weights $w_{k}$ for $n=5$ , 10 are shown in Tables 3.5.1 and 3.5.2. The $p_{n}(x)$ are the monic Legendre polynomials, that is, the polynomials $\mathop{P_{{n}}\/}\nolimits\!\left(x\right)$ (§18.3) scaled so that the coefficient of the highest power of $x$ in their explicit forms is unity.

Table 3.5.1: Nodes and weights for the 5-point Gauss–Legendre formula.

$\pm x_{k}$		$w_{k}$
0.00000 00000 00000		0.56888 88888 88889
0.53846 93101 05683		0.47862 86704 99366
0.90617 98459 38664		0.23692 68850 56189

Symbols:: $w_{k}$ : weights
Referenced by:: ¶ ‣ §3.5(v), §3.5(vi)
Permalink:: http://dlmf.nist.gov/3.5.T1

Table 3.5.2: Nodes and weights for the 10-point Gauss–Legendre formula.

$\pm x_{k}$	$w_{k}$
0.14887 43389 81631 211	0.29552 42247 14752 870
0.43339 53941 29247 191	0.26926 67193 09996 355
0.67940 95682 99024 406	0.21908 63625 15982 044
0.86506 33666 88984 511	0.14945 13491 50580 593
0.97390 65285 17171 720	0.06667 13443 08688 138

Symbols:: $w_{k}$ : weights
Keywords:: Legendre polynomials
Referenced by:: ¶ ‣ §3.5(v)
Permalink:: http://dlmf.nist.gov/3.5.T2

Table 3.5.3: Nodes and weights for the 20-point Gauss–Legendre formula.

$\pm x_{k}$	$w_{k}$
0.07652 65211 33497 33375 5	0.15275 33871 30725 85069 8
0.22778 58511 41645 07808 0	0.14917 29864 72603 74678 8
0.37370 60887 15419 56067 3	0.14209 61093 18382 05132 9
0.51086 70019 50827 09800 4	0.13168 86384 49176 62689 8
0.63605 36807 26515 02545 3	0.11819 45319 61518 41731 2
0.74633 19064 60150 79261 4	0.10193 01198 17240 43503 7
0.83911 69718 22218 82339 5	0.08327 67415 76704 74872 5
0.91223 44282 51325 90586 8	0.06267 20483 34109 06357 0
0.96397 19272 77913 79126 8	0.04060 14298 00386 94133 1
0.99312 85991 85094 92478 6	0.01761 40071 39152 11831 2

Symbols:: $w_{k}$ : weights
Keywords:: Legendre polynomials
Permalink:: http://dlmf.nist.gov/3.5.T3

Table 3.5.4: Nodes and weights for the 40-point Gauss–Legendre formula.

$\pm x_{k}$	$w_{k}$
0.03877 24175 06050 82193 3	0.07750 59479 78424 81126 4
0.11608 40706 75255 20848 3	0.07703 98181 64247 96558 8
0.19269 75807 01371 09971 6	0.07611 03619 00626 24237 2
0.26815 21850 07253 68114 1	0.07472 31690 57968 26420 0
0.34199 40908 25758 47300 7	0.07288 65823 95804 05906 1
0.41377 92043 71605 00152 5	0.07061 16473 91286 77969 6
0.48307 58016 86178 71290 9	0.06791 20458 15233 90382 6
0.54946 71250 95128 20207 6	0.06480 40134 56601 03807 5
0.61255 38896 67980 23795 3	0.06130 62424 92928 93916 7
0.67195 66846 14179 54837 9	0.05743 97690 99391 55136 7
0.72731 82551 89927 10328 1	0.05322 78469 83936 82435 5
0.77830 56514 26519 38769 5	0.04869 58076 35072 23206 1
0.82461 22308 33311 66319 6	0.04387 09081 85673 27199 2
0.86595 95032 12259 50382 1	0.03878 21679 74472 01764 0
0.90209 88069 68874 29672 8	0.03346 01952 82547 84739 3
0.93281 28082 78676 53336 1	0.02793 70069 80023 40109 9
0.95791 68192 13791 65580 5	0.02224 58491 94166 95726 2
0.97725 99499 83774 26266 3	0.01642 10583 81907 88871 3
0.99072 62386 99457 00645 3	0.01049 82845 31152 81361 5
0.99823 77097 10559 20035 0	0.00452 12770 98533 19125 8

Symbols:: $w_{k}$ : weights
Keywords:: Legendre polynomials
Permalink:: http://dlmf.nist.gov/3.5.T4

Table 3.5.5: Nodes and weights for the 80-point Gauss–Legendre formula.

$\pm x_{k}$	$w_{k}$
0.01951 13832 56793 99765 4	0.03901 78136 56306 65481 1
0.05850 44371 52420 66862 9	0.03895 83959 62769 53119 9
0.09740 83984 41584 59906 3	0.03883 96510 59051 96893 2
0.13616 40228 09143 88655 9	0.03866 17597 74076 46332 7
0.17471 22918 32646 81255 9	0.03842 49930 06959 42318 5
0.21299 45028 57666 13257 2	0.03812 97113 14477 63834 4
0.25095 23583 92272 12049 3	0.03777 63643 62001 39749 0
0.28852 80548 84511 85310 9	0.03736 54902 38730 49002 7
0.32566 43707 47701 91461 9	0.03689 77146 38276 00883 9
0.36230 47534 99487 31561 9	0.03637 37499 05835 97804 4
0.39839 34058 81969 22702 4	0.03579 43939 53416 05460 3
0.43387 53708 31756 09306 2	0.03516 05290 44747 59349 6
0.46869 66151 70544 47703 6	0.03447 31204 51753 92879 4
0.50280 41118 88784 98759 4	0.03373 32149 84611 52281 7
0.53614 59208 97131 93202 0	0.03294 19393 97645 40138 3
0.56867 12681 22709 78472 5	0.03210 04986 73487 77314 8
0.60033 06228 29751 74315 5	0.03121 01741 88114 70164 2
0.63107 57730 46871 96624 8	0.03027 23217 59557 98066 1
0.66085 98989 86119 80173 6	0.02928 83695 83267 84769 3
0.68963 76443 42027 60077 1	0.02825 98160 57276 86239 7
0.71736 51853 62099 88025 4	0.02718 82275 00486 38067 4
0.74400 02975 83597 27231 7	0.02607 52357 67565 11790 3
0.76950 24201 35041 37386 6	0.02492 25357 64115 49110 5
0.79383 27175 04605 44994 9	0.02373 18828 65930 10129 3
0.81695 41386 81463 47037 1	0.02250 50902 46332 46192 6
0.83883 14735 80255 27561 7	0.02124 40261 15782 00638 9
0.85943 14066 63111 09697 7	0.01995 06108 78141 99892 9
0.87872 25676 78213 82870 4	0.01862 68142 08299 03142 9
0.89667 55794 38770 68319 4	0.01727 46520 56269 30635 9
0.91326 31025 71757 65416 5	0.01589 61835 83725 68804 5
0.92845 98771 72445 79595 3	0.01449 35080 40509 07611 7
0.94224 27613 09872 67475 2	0.01306 87615 92401 33929 4
0.95459 07663 43634 90549 3	0.01162 41141 20797 82691 7
0.96548 50890 43799 25145 2	0.01016 17660 41103 06452 1
0.97490 91405 85727 79338 6	0.00868 39452 69260 85842 6
0.98284 85727 38629 07041 8	0.00719 29047 68117 31275 3
0.98929 13024 99755 53102 7	0.00569 09224 51403 19864 9
0.99422 75409 65688 27789 2	0.00418 03131 24694 89523 7
0.99764 98643 98237 68889 9	0.00266 35335 89512 68166 9
0.99955 38226 51630 62988 0	0.00114 49500 03186 94153 5

Symbols:: $w_{k}$ : weights
Keywords:: Legendre polynomials
Permalink:: http://dlmf.nist.gov/3.5.T5

¶ Gauss–Chebyshev Formula

Keywords:: Chebyshev polynomials, Gauss quadrature

3.5.22

$[a,b]=[-1,1],$

$w(x)=(1-x^{2})^{{-1/2}},$

$\gamma _{n}=\frac{\pi}{2^{{2n-1}}}.$

Symbols:: $[a,b]$ : closed interval, $\gamma _{n}$ : coefficients and $w$ : weight
Permalink:: http://dlmf.nist.gov/3.5.E22
Encodings:: TeX, TeX, TeX, pMML, pMML, pMML, png, png, png

The nodes $x_{k}$ and weights $w_{k}$ are known explicitly:

3.5.23

$x_{k}=\mathop{\cos\/}\nolimits\!\left(\frac{2k-1}{2n}\pi\right),$

$w_{k}=\frac{\pi}{n}$ , $k=1,2,\dots,n$ .

Symbols:: $\mathop{\cos\/}\nolimits z$ : cosine function and $w_{k}$ : weights
A&S Ref:: 25.4.38
Permalink:: http://dlmf.nist.gov/3.5.E23
Encodings:: TeX, TeX, pMML, pMML, png, png

In the case of Chebyshev weight functions $w(x)=(1-x)^{\alpha}(1+x)^{\beta}$ on $[-1,1]$ , with $\left|\alpha\right|=\left|\beta\right|=\frac{1}{2}$ , the nodes $x_{k}$ , weights $w_{k}$ , and error constant $\gamma _{n}$ , are as follows:

3.5.24

$x_{k}=\mathop{\cos\/}\nolimits\!\left(\frac{k}{n+1}\pi\right),$

$w_{k}=\frac{\pi}{n+1}{\mathop{\sin\/}\nolimits^{{2}}}\!\left(\frac{k}{n+1}\pi\right),$

$\gamma _{n}=\frac{\pi}{2^{{2n+1}}},$ $\alpha=\beta=\tfrac{1}{2}$ ,

Symbols:: $\mathop{\cos\/}\nolimits z$ : cosine function, $\mathop{\sin\/}\nolimits z$ : sine function, $\gamma _{n}$ : coefficients, $\alpha$ : exponent, $\beta$ : exponent and $w_{k}$ : weights
A&S Ref:: 25.4.40 (with corrected nodes and weights)
Permalink:: http://dlmf.nist.gov/3.5.E24
Encodings:: TeX, TeX, TeX, pMML, pMML, pMML, png, png, png

and

3.5.25

$x_{k}=\pm\mathop{\cos\/}\nolimits\!\left(\frac{2k}{2n+1}\pi\right),$

$w_{k}=\frac{4\pi}{2n+1}{\mathop{\sin\/}\nolimits^{{2}}}\!\left(\frac{k}{2n+1}\pi\right),$

$\gamma _{n}=\frac{\pi}{2^{{2n}}},$ $\alpha=-\beta=\pm\tfrac{1}{2}$ ,

Symbols:: $\mathop{\cos\/}\nolimits z$ : cosine function, $\mathop{\sin\/}\nolimits z$ : sine function, $\gamma _{n}$ : coefficients, $\alpha$ : exponent, $\beta$ : exponent and $w_{k}$ : weights
A&S Ref:: 25.4.42 and 25.4.43 (in different form)
Permalink:: http://dlmf.nist.gov/3.5.E25
Encodings:: TeX, TeX, TeX, pMML, pMML, pMML, png, png, png

where $k=1,2,\dots,n$ .

¶ Gauss–Jacobi Formula

Keywords:: Gauss quadrature, Jacobi polynomials

3.5.26

$[a,b]=[-1,1],$

$w(x)=(1-x)^{\alpha}(1+x)^{\beta},$

$\gamma _{n}=\dfrac{\mathop{\Gamma\/}\nolimits\!\left(n+\alpha+1\right)\mathop{\Gamma\/}\nolimits\!\left(n+\beta+1\right)\mathop{\Gamma\/}\nolimits\!\left(n+\alpha+\beta+1\right)}{(2n+\alpha+\beta+1)(\mathop{\Gamma\/}\nolimits\!\left(2n+\alpha+\beta+1\right))^{2}}2^{{2n+\alpha+\beta+1}}n!,$ $\alpha>-1$ , $\beta>-1$ .

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, $[a,b]$ : closed interval, $!$ : $n!$ : factorial, $\gamma _{n}$ : coefficients, $\alpha$ : exponent, $\beta$ : exponent and $w$ : weight
Permalink:: http://dlmf.nist.gov/3.5.E26
Encodings:: TeX, TeX, TeX, pMML, pMML, pMML, png, png, png

The $p_{n}(x)$ are the monic Jacobi polynomials $\mathop{P^{{(\alpha,\beta)}}_{{n}}\/}\nolimits\!\left(x\right)$ (§18.3).

¶ Gauss–Laguerre Formula

Keywords:: Gauss quadrature, Laguerre polynomials

3.5.27

$[a,b)=[0,\infty),$

$w(x)=x^{\alpha}e^{{-x}},$

$\gamma _{n}=n!\,\mathop{\Gamma\/}\nolimits\!\left(n+\alpha+1\right),$ $\alpha>-1$ .

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, $[a,b)$ : half-closed interval, $e$ : base of exponential function, $!$ : $n!$ : factorial, $\gamma _{n}$ : coefficients, $\alpha$ : exponent and $w$ : weight
A&S Ref:: 25.4.45 (in more general form)
Permalink:: http://dlmf.nist.gov/3.5.E27
Encodings:: TeX, TeX, TeX, pMML, pMML, pMML, png, png, png

If $\alpha\neq 0$ this is called the generalized Gauss–Laguerre formula.

The nodes $x_{k}$ and weights $w_{k}$ for $\alpha=0$ and $n=5$ , 10 are shown in Tables 3.5.6 and 3.5.7. The $p_{n}(x)$ are the monic Laguerre polynomials $\mathop{L_{{n}}\/}\nolimits\!\left(x\right)$ (§18.3).

Table 3.5.6: Nodes and weights for the 5-point Gauss–Laguerre formula.

$x_{k}$		$w_{k}$
0.26356 03197 18141		0.52175 56105 82809
0.14134 03059 10652	×10¹	0.39866 68110 83176
0.35964 25771 04072	×10¹	0.75942 44968 17076	×10⁻¹
0.70858 10005 85884	×10¹	0.36117 58679 92205	×10⁻²
0.12640 80084 42758	×10²	0.23369 97238 57762	×10⁻⁴

Symbols:: $w_{k}$ : weights
Keywords:: Laguerre polynomials
Referenced by:: ¶ ‣ §3.5(v)
Permalink:: http://dlmf.nist.gov/3.5.T6

Table 3.5.7: Nodes and weights for the 10-point Gauss–Laguerre formula.

$x_{k}$		$w_{k}$
0.13779 34705 40492 431		0.30844 11157 65020 141
0.72945 45495 03170 498		0.40111 99291 55273 552
0.18083 42901 74031 605	×10¹	0.21806 82876 11809 422
0.34014 33697 85489 951	×10¹	0.62087 45609 86777 475	×10⁻¹
0.55524 96140 06380 363	×10¹	0.95015 16975 18110 055	×10⁻²
0.83301 52746 76449 670	×10¹	0.75300 83885 87538 775	×10⁻³
0.11843 78583 79000 656	×10²	0.28259 23349 59956 557	×10⁻⁴
0.16279 25783 13781 021	×10²	0.42493 13984 96268 637	×10⁻⁶
0.21996 58581 19807 620	×10²	0.18395 64823 97963 078	×10⁻⁸
0.29920 69701 22738 916	×10²	0.99118 27219 60900 856	×10⁻¹²

Symbols:: $w_{k}$ : weights
Keywords:: Laguerre polynomials
Referenced by:: ¶ ‣ §3.5(v)
Permalink:: http://dlmf.nist.gov/3.5.T7

Table 3.5.8: Nodes and weights for the 15-point Gauss–Laguerre formula.

$x_{k}$		$w_{k}$
0.93307 81201 72818 04762 9	×10⁻¹	0.21823 48859 40086 88985 6
0.49269 17403 01883 90896 0		0.34221 01779 22883 32963 9
0.12155 95412 07094 94637 3	×10¹	0.26302 75779 41680 09741 5
0.22699 49526 20374 32024 7	×10¹	0.12642 58181 05930 53584 3
0.36676 22721 75143 72772 5	×10¹	0.40206 86492 10009 14841 6	×10⁻¹
0.54253 36627 41355 31653 4	×10¹	0.85638 77803 61183 83639 2	×10⁻²
0.75659 16226 61306 78605 0	×10¹	0.12124 36147 21425 20762 2	×10⁻²
0.10120 22856 80191 12734 8	×10²	0.11167 43923 44251 94199 3	×10⁻³
0.13130 28248 21757 23564 1	×10²	0.64599 26762 02290 09246 5	×10⁻⁵
0.16654 40770 83299 57822 5	×10²	0.22263 16907 09627 26303 3	×10⁻⁶
0.20776 47889 94487 66772 9	×10²	0.42274 30384 97936 50073 5	×10⁻⁸
0.25623 89422 67287 80144 6	×10²	0.39218 97267 04108 92903 8	×10⁻¹⁰
0.31407 51916 97539 38515 2	×10²	0.14565 15264 07312 64063 3	×10⁻¹²
0.38530 68330 64860 09416 3	×10²	0.14830 27051 11330 13354 6	×10⁻¹⁵
0.48026 08557 26857 94346 6	×10²	0.16005 94906 21113 32310 5	×10⁻¹⁹

Symbols:: $w_{k}$ : weights
Keywords:: Laguerre polynomials
Permalink:: http://dlmf.nist.gov/3.5.T8

Table 3.5.9: Nodes and weights for the 20-point Gauss–Laguerre formula.

$x_{k}$		$w_{k}$
0.70539 88969 19887 53366 7	×10⁻¹	0.16874 68018 51113 86214 9
0.37212 68180 01611 44379 4		0.29125 43620 06068 28171 7
0.91658 21024 83273 56466 8		0.26668 61028 67001 28855 0
0.17073 06531 02834 38806 9	×10¹	0.16600 24532 69506 84003 1
0.27491 99255 30943 21296 5	×10¹	0.74826 06466 87923 70540 1	×10⁻¹
0.40489 25313 85088 69223 7	×10¹	0.24964 41730 92832 21072 8	×10⁻¹
0.56151 74970 86161 65141 0	×10¹	0.62025 50844 57223 68474 5	×10⁻²
0.74590 17453 67106 33097 7	×10¹	0.11449 62386 47690 82420 4	×10⁻²
0.95943 92869 58109 67724 7	×10¹	0.15574 17730 27811 97478 0	×10⁻³
0.12038 80254 69643 16309 6	×10²	0.15401 44086 52249 15689 4	×10⁻⁴
0.14814 29344 26307 39978 5	×10²	0.10864 86366 51798 23514 8	×10⁻⁵
0.17948 89552 05193 76017 4	×10²	0.53301 20909 55671 47509 3	×10⁻⁷
0.21478 78824 02850 10975 7	×10²	0.17579 81179 05058 20035 8	×10⁻⁸
0.25451 70279 31869 05503 5	×10²	0.37255 02402 51232 08726 3	×10⁻¹⁰
0.29932 55463 17006 12006 7	×10²	0.47675 29251 57819 05244 9	×10⁻¹²
0.35013 43424 04790 00006 3	×10²	0.33728 44243 36243 84123 7	×10⁻¹⁴
0.40833 05705 67285 71062 0	×10²	0.11550 14339 50039 88309 6	×10⁻¹⁶
0.47619 99404 73465 02139 9	×10²	0.15395 22140 58234 35534 6	×10⁻¹⁹
0.55810 79575 00638 98890 8	×10²	0.52864 42725 56915 78288 0	×10⁻²³
0.66524 41652 56157 53818 6	×10²	0.16564 56612 49902 32959 1	×10⁻²⁷

Symbols:: $w_{k}$ : weights
Keywords:: Laguerre polynomials
Permalink:: http://dlmf.nist.gov/3.5.T9

¶ Gauss–Hermite Formula

Keywords:: Gauss quadrature, Hermite polynomials

3.5.28

$(a,b)=(-\infty,\infty),$

$w(x)=e^{{-x^{2}}},$

$\gamma _{n}=\sqrt{\pi}\,\frac{n!}{2^{n}}.$

Symbols:: $e$ : base of exponential function, $!$ : $n!$ : factorial, $(a,b)$ : open interval, $\gamma _{n}$ : coefficients and $w$ : weight
A&S Ref:: 25.4.46
Permalink:: http://dlmf.nist.gov/3.5.E28
Encodings:: TeX, TeX, TeX, pMML, pMML, pMML, png, png, png

The nodes $x_{k}$ and weights $w_{k}$ for $n=5,10$ are shown in Tables 3.5.10 and 3.5.11. The $p_{n}(x)$ are the monic Hermite polynomials $\mathop{H_{{n}}\/}\nolimits\!\left(x\right)$ (§18.3).

Table 3.5.10: Nodes and weights for the 5-point Gauss–Hermite formula.

$\pm x_{k}$		$w_{k}$
0.00000 00000 00000		0.94530 87204 82942
0.95857 24646 13819		0.39361 93231 52241
0.20201 82870 45609	×10¹	0.19953 24205 90459	×10⁻¹

Symbols:: $w_{k}$ : weights
Keywords:: Hermite polynomials
Referenced by:: ¶ ‣ §3.5(v)
Permalink:: http://dlmf.nist.gov/3.5.T10

Table 3.5.11: Nodes and weights for the 10-point Gauss–Hermite formula.

$\pm x_{k}$		$w_{k}$
0.34290 13272 23704 609		0.61086 26337 35325 799
0.10366 10829 78951 365	×10¹	0.24013 86110 82314 686
0.17566 83649 29988 177	×10¹	0.33874 39445 54810 631	×10⁻¹
0.25327 31674 23278 980	×10¹	0.13436 45746 78123 269	×10⁻²
0.34361 59118 83773 760	×10¹	0.76404 32855 23262 063	×10⁻⁵

Symbols:: $w_{k}$ : weights
Keywords:: Hermite polynomials
Referenced by:: ¶ ‣ §3.5(v)
Permalink:: http://dlmf.nist.gov/3.5.T11

Table 3.5.12: Nodes and weights for the 15-point Gauss–Hermite formula.

$\pm x_{k}$		$w_{k}$
0.00000 00000 00000 00000 0		0.56410 03087 26417 53285 3
0.56506 95832 55575 74852 6		0.41202 86874 98898 62702 6
0.11361 15585 21092 06663 2	×10¹	0.15848 89157 95935 74688 4
0.17199 92575 18648 89324 2	×10¹	0.30780 03387 25460 82228 7	×10⁻¹
0.23257 32486 17385 77454 5	×10¹	0.27780 68842 91277 58960 8	×10⁻²
0.29671 66927 90560 32484 9	×10¹	0.10000 44412 32499 86812 7	×10⁻³
0.36699 50373 40445 25347 3	×10¹	0.10591 15547 71106 66357 8	×10⁻⁵
0.44999 90707 30939 15536 6	×10¹	0.15224 75804 25351 70201 6	×10⁻⁸

Symbols:: $w_{k}$ : weights
Keywords:: Hermite polynomials
Permalink:: http://dlmf.nist.gov/3.5.T12

Table 3.5.13: Nodes and weights for the 20-point Gauss–Hermite formula.

$\pm x_{k}$		$w_{k}$
0.24534 07083 00901 24990 4		0.46224 36696 00610 08965 0
0.73747 37285 45394 35870 6		0.28667 55053 62834 12972 0
0.12340 76215 39532 30078 9	×10¹	0.10901 72060 20023 32001 4
0.17385 37712 11658 62067 8	×10¹	0.24810 52088 74636 10882 2	×10⁻¹
0.22549 74002 08927 55230 8	×10¹	0.32437 73342 23786 18321 8	×10⁻²
0.27888 06058 42813 04805 3	×10¹	0.22833 86360 16353 96725 7	×10⁻³
0.33478 54567 38321 63269 1	×10¹	0.78025 56478 53206 36941 5	×10⁻⁵
0.39447 64040 11562 52103 8	×10¹	0.10860 69370 76928 16940 0	×10⁻⁶
0.46036 82449 55074 42730 8	×10¹	0.43993 40992 27318 05536 3	×10⁻⁹
0.53874 80890 01123 28620 2	×10¹	0.22293 93645 53415 12925 2	×10⁻¹²

Symbols:: $w_{k}$ : weights
Keywords:: Hermite polynomials
Referenced by:: §3.5(vi)
Permalink:: http://dlmf.nist.gov/3.5.T13

¶ Gauss Formula for a Logarithmic Weight Function

Keywords:: Gauss quadrature, weight functions

3.5.29

$[a,b]=[0,1],$

$w(x)=\mathop{\ln\/}\nolimits\!\left(1/x\right).$

Symbols:: $[a,b]$ : closed interval, $\mathop{\ln\/}\nolimits z$ : principal branch of logarithm function and $w$ : weight
A&S Ref:: 25.4.44 (modification of)
Permalink:: http://dlmf.nist.gov/3.5.E29
Encodings:: TeX, TeX, pMML, pMML, png, png

The nodes $x_{k}$ and weights $w_{k}$ for $n=5,10$ are shown in Tables 3.5.14 and 3.5.15.

Table 3.5.14: Nodes and weights for the 5-point Gauss formula for the logarithmic weight function.

$x_{k}$		$w_{k}$
0.29134 47215 19721	×10⁻¹	0.29789 34717 82894
0.17397 72133 20898		0.34977 62265 13224
0.41170 25202 84902		0.23448 82900 44052
0.67731 41745 82820		0.98930 45951 66331	×10⁻¹
0.89477 13610 31008		0.18911 55214 31958	×10⁻¹

Symbols:: $w_{k}$ : weights
Referenced by:: ¶ ‣ §3.5(v)
Permalink:: http://dlmf.nist.gov/3.5.T14

Table 3.5.15: Nodes and weights for the 10-point Gauss formula for the logarithmic weight function.

$x_{k}$		$w_{k}$
0.90426 30962 19965 064	×10⁻²	0.12095 51319 54570 515
0.53971 26622 25006 295	×10⁻¹	0.18636 35425 64071 870
0.13531 18246 39250 775		0.19566 08732 77759 983
0.24705 24162 87159 824		0.17357 71421 82906 921
0.38021 25396 09332 334		0.13569 56729 95484 202
0.52379 23179 71843 201		0.93646 75853 81105 260	×10⁻¹
0.66577 52055 16424 597		0.55787 72735 14158 741	×10⁻¹
0.79419 04160 11966 217		0.27159 81089 92333 311	×10⁻¹
0.89816 10912 19003 538		0.95151 82602 84851 500	×10⁻²
0.96884 79887 18633 539		0.16381 57633 59826 325	×10⁻²

Symbols:: $w_{k}$ : weights
Referenced by:: ¶ ‣ §3.5(v)
Permalink:: http://dlmf.nist.gov/3.5.T15

Table 3.5.16: Nodes and weights for the 15-point Gauss formula for the logarithmic weight function.

$x_{k}$		$w_{k}$
0.43831 10175 47540 38348 5	×10⁻²	0.67009 97891 64937 13603 2	×10⁻¹
0.25935 89810 53306 16102 3	×10⁻¹	0.11226 41502 86705 74182 8
0.65596 09541 23162 45254 1	×10⁻¹	0.13176 01770 39679 90373 2
0.12210 19340 73331 60333 0		0.13521 76490 61934 72513 2
0.19339 52623 74007 11598 3		0.12788 17986 45680 37040 1
0.27677 28387 06102 02439 4		0.11353 29074 90219 42129 0
0.36901 51271 39742 94381 6		0.95205 23978 43586 58511 6	×10⁻¹
0.46652 43289 64706 58267 6		0.75389 31416 73959 54339 3	×10⁻¹
0.56547 34737 91817 30642 5		0.56078 42449 26537 17992 3	×10⁻¹
0.66196 29190 12456 42139 0		0.38768 29537 50182 31110 0	×10⁻¹
0.75217 88833 78785 79878 8		0.24451 48326 87500 75960 4	×10⁻¹
0.83254 80338 66189 58925 7		0.13624 63013 82388 46905 4	×10⁻¹
0.89988 20501 20898 08433 0		0.63164 47598 59076 11998 3	×10⁻²
0.95150 61887 43409 90272 6		0.21388 89915 94447 13478 3	×10⁻²
0.98536 44681 22131 93892 7		0.36061 38183 35406 64685 1	×10⁻³

Symbols:: $w_{k}$ : weights
Permalink:: http://dlmf.nist.gov/3.5.T16

Table 3.5.17: Nodes and weights for the 20-point Gauss formula for the logarithmic weight function.

$x_{k}$		$w_{k}$
0.25883 27955 92195 54283 3	×10⁻²	0.43142 75213 32080 78579 0	×10⁻¹
0.15209 66234 95602 31720 7	×10⁻¹	0.75383 70990 85893 59550 5	×10⁻¹
0.38536 55037 21653 27959 8	×10⁻¹	0.93053 26745 16630 51372 7	×10⁻¹
0.72181 61381 58739 06435 0	×10⁻¹	0.10145 67118 49829 75443 7
0.11546 05264 87633 15055 9		0.10320 17620 56072 06905 8
0.16744 28562 75329 68571 8		0.10002 25498 05273 16653 3
0.22698 37872 60202 50336 1		0.93259 79930 02976 78083 7	×10⁻¹
0.29275 49609 41545 83299 2		0.84028 95287 19410 56497 1	×10⁻¹
0.36327 74298 57858 90453 8		0.73285 58913 00307 40962 8	×10⁻¹
0.43695 71400 90768 31848 7		0.61850 33691 37302 89957 2	×10⁻¹
0.51212 25946 78967 33619 6		0.50416 60443 83746 77637 1	×10⁻¹
0.58706 40449 14409 91513 2		0.39551 37000 52983 85332 9	×10⁻¹
0.66007 34133 14909 41391 2		0.29694 07789 58128 44804 6	×10⁻¹
0.72948 40839 29687 49887 1		0.21156 31535 54270 97673 0	×10⁻¹
0.79370 96719 87085 81774 4		0.14123 73293 89640 20436 6	×10⁻¹
0.85128 08927 89125 72722 2		0.86609 74504 33549 86282 3	×10⁻²
0.90087 96808 54417 59422 3		0.47199 40146 20360 49543 7	×10⁻²
0.94136 97491 29091 67630 3		0.21513 97403 96520 61146 8	×10⁻²
0.97182 27410 75263 19373 8		0.71972 82146 53202 64635 8	×10⁻³
0.99153 80814 38711 97265 2		0.12042 76763 30216 74169 3	×10⁻³

Symbols:: $w_{k}$ : weights
Permalink:: http://dlmf.nist.gov/3.5.T17

§3.5(vi) Eigenvalue/Eigenvector Characterization of Gauss Quadrature Formulas

Notes:: See Davis and Rabinowitz (1984, pp. 118–120) and Golub and Welsch (1969).
Keywords:: Gauss quadrature, matrix
Referenced by:: ¶ ‣ §3.8(iii)
Permalink:: http://dlmf.nist.gov/3.5.vi

All the monic orthogonal polynomials $\{ p_{n}\}$ used with Gauss quadrature satisfy a three-term recurrence relation (§18.2(iv)):

3.5.30 $p_{{k+1}}(x)=(x-\alpha _{k})p_{k}(x)-\beta _{k}p_{{k-1}}(x),$ $k=0,1,\dots$ ,

Symbols:: $p_{n}$ : set of monic polynomials
A&S Ref:: 22.1.4 (for monic polynomials)
Permalink:: http://dlmf.nist.gov/3.5.E30
Encodings:: TeX, pMML, png

with $\beta _{k}>0$ , $p_{{-1}}(x)=0$ , and $p_{0}(x)=1$ .

The Gauss nodes $x_{k}$ (the zeros of $p_{n}$ ) are the eigenvalues of the (symmetric tridiagonal) Jacobi matrix of order $n\times n$ :

3.5.31 $\mathbf{J}_{n}=\begin{bmatrix}\alpha _{0}&\sqrt{\beta _{1}}&&&0\\ \sqrt{\beta _{1}}&\alpha _{1}&\sqrt{\beta _{2}}&&\\ &\ddots&\ddots&\ddots&\\ &&\sqrt{\beta _{{n-2}}}&\alpha _{{n-2}}&\sqrt{\beta _{{n-1}}}\\ 0&&&\sqrt{\beta _{{n-1}}}&\alpha _{{n-1}}\end{bmatrix}.$

Permalink:: http://dlmf.nist.gov/3.5.E31
Encodings:: TeX, pMML, png

Let $\mathbf{v}_{k}$ denote the normalized eigenvector of $\mathbf{J}_{n}$ corresponding to the eigenvalue $x_{k}$ . Then the weights are given by

3.5.32 $w_{k}=\beta _{0}v_{{k,1}}^{2},$ $k=1,2,\dots,n$ ,

Symbols:: $\mathbf{v}_{k}$ : normalized eigenvector and $w_{k}$ : weights
Permalink:: http://dlmf.nist.gov/3.5.E32
Encodings:: TeX, pMML, png

where $\beta _{0}=\int _{a}^{b}w(x)dx$ and $v_{{k,1}}$ is the first element of $\mathbf{v}_{k}$ . Also, the error constant (3.5.20) is given by

3.5.33 $\gamma _{n}=\beta _{0}\beta _{1}\cdots\beta _{n}.$

Symbols:: $\gamma _{n}$ : coefficients
Permalink:: http://dlmf.nist.gov/3.5.E33
Encodings:: TeX, pMML, png

Tables 3.5.1–3.5.13 can be verified by application of the results given in the present subsection. In these cases the coefficients $\alpha _{k}$ and $\beta _{k}$ are obtainable explicitly from results given in §18.9(i).

§3.5(vii) Oscillatory Integrals

Keywords:: Clenshaw–Curtis quadrature formula, quadrature
Permalink:: http://dlmf.nist.gov/3.5.vii

Integrals of the form

3.5.34

$\int _{a}^{b}f(x)\mathop{\cos\/}\nolimits\!\left(\omega x\right)dx,$

$\int _{a}^{b}f(x)\mathop{\sin\/}\nolimits\!\left(\omega x\right)dx,$

Symbols:: $\mathop{\cos\/}\nolimits z$ : cosine function, $dx$ : differential of $x$ , $\int$ : integral and $\mathop{\sin\/}\nolimits z$ : sine function
Permalink:: http://dlmf.nist.gov/3.5.E34
Encodings:: TeX, TeX, pMML, pMML, png, png

can be computed by Filon’s rule. See Davis and Rabinowitz (1984, pp. 146–168).

Oscillatory integral transforms are treated in Wong (1982) by a method based on Gaussian quadrature. A comparison of several methods, including an extension of the Clenshaw–Curtis formula (§3.5(iv)), is given in Evans and Webster (1999).

For computing infinite oscillatory integrals, Longman’s method may be used. The integral is written as an alternating series of positive and negative subintegrals that are computed individually; see Longman (1956). Convergence acceleration schemes, for example Levin’s transformation (§3.9(v)), can be used when evaluating the series. Further methods are given in Clendenin (1966) and Lyness (1985).

For a comprehensive survey of quadrature of highly oscillatory integrals, including multidimensional integrals, see Iserles et al. (2006).

§3.5(viii) Complex Gauss Quadrature

Notes:: See Salzer (1955).
Keywords:: Bessel polynomials, Bromwich integral, Gauss quadrature, nodes, orthogonal polynomials, quadrature, weight functions
Referenced by:: §11.13(iii), ¶ ‣ §3.5(ix)
Permalink:: http://dlmf.nist.gov/3.5.viii

For the Bromwich integral

3.5.35 $I(f)=\frac{1}{2\pi i}\int _{{c-i\infty}}^{{c+i\infty}}e^{\zeta}\zeta^{{-s}}f(\zeta)d\zeta,$ $s>0$ , $c>c_{0}>0$ ,

Symbols:: $dx$ : differential of $x$ , $e$ : base of exponential function, $\int$ : integral and $I(f)$ : Bromwich integral
Referenced by:: ¶ ‣ §3.5(viii), ¶ ‣ §3.5(ix), §3.5(viii)
Permalink:: http://dlmf.nist.gov/3.5.E35
Encodings:: TeX, pMML, png

a complex Gauss quadrature formula is available. Here $f(\zeta)$ is assumed analytic in the half-plane $\realpart{\zeta}>c_{0}$ and bounded as $\zeta\to\infty$ in $\left|\mathop{\mathrm{ph}\/}\nolimits\zeta\right|\leq\frac{1}{2}\pi$ . The quadrature rule for (3.5.35) is

3.5.36 $I(f)=\sum _{{k=1}}^{n}w_{k}f(\zeta _{k})+E_{n}(f),$

Symbols:: $I(f)$ : Bromwich integral, $\zeta _{k}$ : Gauss nodes, $E_{n}(f)$ : error term and $w_{k}$ : weights
Referenced by:: ¶ ‣ §3.5(viii), §3.5(viii)
Permalink:: http://dlmf.nist.gov/3.5.E36
Encodings:: TeX, pMML, png

where $E_{n}(f)=0$ if $f(\zeta)$ is a polynomial of degree $\leq 2n-1$ in $1/\zeta$ . Complex orthogonal polynomials $p_{n}(1/\zeta)$ of degree $n=0,1,2,\dots$ , in $1/\zeta$ that satisfy the orthogonality condition

3.5.37 $\int _{{c-i\infty}}^{{c+i\infty}}e^{\zeta}\zeta^{{-s}}p_{k}(1/\zeta)p_{\ell}(1/\zeta)d\zeta=0,$ $k\neq\ell$ ,

Symbols:: $dx$ : differential of $x$ , $e$ : base of exponential function, $\int$ : integral and $p_{n}(1/\zeta)$ : orthogonal polynomials
Permalink:: http://dlmf.nist.gov/3.5.E37
Encodings:: TeX, pMML, png

are related to Bessel polynomials (§§10.49(ii) and 18.34). The complex Gauss nodes $\zeta _{k}$ have positive real part for all $s>0$ .

The nodes and weights of the 5-point complex Gauss quadrature formula (3.5.36) for $s=1$ are shown in Table 3.5.18. Extensive tables of quadrature nodes and weights can be found in Krylov and Skoblya (1985).

Table 3.5.18: Nodes and weights for the 5-point complex Gauss quadrature formula with $s=1$ .

$\zeta _{k}$			$w_{k}$
3.65569 4325	$+$	$6.54373\; 6899i$	3.83966 1630	$-$	$0.27357\; 0 3863i$
3.65569 4325	$-$	$6.54373\; 6899i$	3.83966 1630	$+$	$0.27357\; 0 3863i$
5.70095 3299	$+$	$3.21026\; 5600i$	−25.07945 221	$+$	$2.18725\; 2294i$
5.70095 3299	$-$	$3.21026\; 5600i$	−25.07945 221	$-$	$2.18725\; 2294i$
6.28670 4752	$+$	$0.00000\; 0 0 0 0 i$	43.47958 116	$+$	$0.00000\; 0 0 0 0 i$

Symbols:: $\zeta _{k}$ : Gauss nodes and $w_{k}$ : weights
Referenced by:: ¶ ‣ §3.5(viii), §3.5(viii)
Permalink:: http://dlmf.nist.gov/3.5.T18

¶ Example. Laplace Transform Inversion

Keywords:: Bessel functions, Laplace transform

From §1.14(iii)

3.5.38 $G(p)=\int _{0}^{\infty}e^{{-pt}}g(t)dt,$

Symbols:: $dx$ : differential of $x$ , $e$ : base of exponential function, $\int$ : integral, $g(t)$ : function and $G(p)$ : Laplace transform of $g(t)$
A&S Ref:: 29.2.1 (in different form)
Permalink:: http://dlmf.nist.gov/3.5.E38
Encodings:: TeX, pMML, png

3.5.39 $g(t)=\frac{1}{2\pi i}\int _{{\sigma-i\infty}}^{{\sigma+i\infty}}e^{{tp}}G(p)dp,$

Symbols:: $dx$ : differential of $x$ , $e$ : base of exponential function, $\int$ : integral, $g(t)$ : function, $G(p)$ : Laplace transform of $g(t)$ and $\sigma$ : parameter
A&S Ref:: 29.2.1 (in different form)
Referenced by:: ¶ ‣ §3.5(viii)
Permalink:: http://dlmf.nist.gov/3.5.E39
Encodings:: TeX, pMML, png

with appropriate conditions. The pair

3.5.40

$g(t)=\mathop{J_{{0}}\/}\nolimits\!\left(t\right),$

$G(p)=\frac{1}{\sqrt{p^{2}+1}},$

Symbols:: $\mathop{J_{{\nu}}\/}\nolimits\!\left(z\right)$ : Bessel function of the first kind, $g(t)$ : function and $G(p)$ : Laplace transform of $g(t)$
Permalink:: http://dlmf.nist.gov/3.5.E40
Encodings:: TeX, TeX, pMML, pMML, png, png

where $\mathop{J_{{0}}\/}\nolimits\!\left(t\right)$ is the Bessel function (§10.2(ii)), satisfy these conditions, provided that $\sigma>0$ . The integral (3.5.39) has the form (3.5.35) if we set $\zeta=tp$ , $c=t\sigma$ , and $f(\zeta)=t^{{-1}}\zeta^{s}G(\zeta/t)$ . We choose $s=1$ so that $f(\zeta)=\mathop{O\/}\nolimits\!\left(1\right)$ at infinity. Equation (3.5.36), without the error term, becomes

3.5.41 $g(t)=\sum _{{k=1}}^{n}\frac{w_{k}\zeta _{k}}{\sqrt{\zeta _{k}^{2}+t^{2}}},$

Symbols:: $\zeta _{k}$ : Gauss nodes, $g(t)$ : function and $w_{k}$ : weights
Permalink:: http://dlmf.nist.gov/3.5.E41
Encodings:: TeX, pMML, png

approximately.

Using Table 3.5.18 we compute $g(t)$ for $n=5$ . The results are given in the middle column of Table 3.5.19, accompanied by the actual 10D values in the last column. Agreement is very good for small values of $t$ , but not for larger values. For these cases the integration path may need to be deformed; see §3.5(ix).

Table 3.5.19: Laplace transform inversion.

$t$	$g(t)$	$\mathop{J_{{0}}\/}\nolimits(t)$
0.0	1.00000 00000	1.00000 00000
0.5	0.93846 98072	0.93846 98072
1.0	0.76519 76866	0.76519 76865
2.0	0.22389 07791	0.22389 10326
5.0	$-$ 0.17759 67713	$-$ 0.17902 54097
10.0	$-$ 0.24593 57645	$-$ 0.07540 53543

Symbols:: $\mathop{J_{{\nu}}\/}\nolimits\!\left(z\right)$ : Bessel function of the first kind and $g(t)$ : function
Referenced by:: ¶ ‣ §3.5(viii)
Permalink:: http://dlmf.nist.gov/3.5.T19

§3.5(ix) Other Contour Integrals

Keywords:: quadrature, steepest-descent paths
Referenced by:: §11.13(iii), ¶ ‣ §3.4(ii), ¶ ‣ §3.5(viii), §3.5(i)
Permalink:: http://dlmf.nist.gov/3.5.ix

A frequent problem with contour integrals is heavy cancellation, which occurs especially when the value of the integral is exponentially small compared with the maximum absolute value of the integrand. To avoid cancellation we try to deform the path to pass through a saddle point in such a way that the maximum contribution of the integrand is derived from the neighborhood of the saddle point. For example, steepest descent paths can be used; see §2.4(iv).

¶ Example

Keywords:: Hilbert transform, Laplace transform, Scorer functions, error functions, quadrature, steepest-descent paths

In (3.5.35) take $s=1$ and $f(\zeta)=e^{{-2\lambda\sqrt{\zeta}}}$ , with $\lambda>0$ . When $\lambda$ is large the integral becomes exponentially small, and application of the quadrature rule of §3.5(viii) is useless. In fact from (7.14.4) and the inversion formula for the Laplace transform (§1.14(iii)) we have

3.5.42 $\mathop{\mathrm{erfc}\/}\nolimits\lambda=\frac{1}{2\pi i}\int _{{c-i\infty}}^{{c+i\infty}}e^{{\zeta-2\lambda\sqrt{\zeta}}}\frac{d\zeta}{\zeta},$ $c>0$ ,

Symbols:: $\mathop{\mathrm{erfc}\/}\nolimits z$ : complementary error function, $dx$ : differential of $x$ , $e$ : base of exponential function, $\int$ : integral and $\lambda$ : parameter
A&S Ref:: 29.3.83 (in different form)
Referenced by:: ¶ ‣ §3.5(ix)
Permalink:: http://dlmf.nist.gov/3.5.E42
Encodings:: TeX, pMML, png

where $\mathop{\mathrm{erfc}\/}\nolimits z$ is the complementary error function, and from (7.12.1) it follows that

3.5.43 $\mathop{\mathrm{erfc}\/}\nolimits\lambda\sim\frac{e^{{-\lambda^{2}}}}{\sqrt{\pi}\lambda},$ $\lambda\to\infty$ .

Symbols:: $\mathop{\mathrm{erfc}\/}\nolimits z$ : complementary error function, $e$ : base of exponential function, $\sim$ : asymptotic equality and $\lambda$ : parameter
Permalink:: http://dlmf.nist.gov/3.5.E43
Encodings:: TeX, pMML, png

With the transformation $\zeta=\lambda^{2}t$ , (3.5.42) becomes

3.5.44 $\mathop{\mathrm{erfc}\/}\nolimits\lambda=\frac{1}{2\pi i}\int _{{c-i\infty}}^{{c+i\infty}}e^{{\lambda^{2}(t-2\sqrt{t})}}\frac{dt}{t},$ $c>0$ ,

Symbols:: $\mathop{\mathrm{erfc}\/}\nolimits z$ : complementary error function, $dx$ : differential of $x$ , $e$ : base of exponential function, $\int$ : integral and $\lambda$ : parameter
Permalink:: http://dlmf.nist.gov/3.5.E44
Encodings:: TeX, pMML, png

with saddle point at $t=1$ , and when $c=1$ the vertical path intersects the real axis at the saddle point. The steepest descent path is given by $\imagpart{(t-2\sqrt{t})}=0$ , or in polar coordinates $t=re^{{i\theta}}$ we have $r={\mathop{\sec\/}\nolimits^{{2}}}\!\left(\frac{1}{2}\theta\right)$ . Thus

3.5.45 $\mathop{\mathrm{erfc}\/}\nolimits\lambda=\frac{e^{{-\lambda^{2}}}}{2\pi}\int _{{-\pi}}^{{\pi}}e^{{-\lambda^{2}{\mathop{\tan\/}\nolimits^{{2}}}\!\left(\frac{1}{2}\theta\right)}}d\theta.$

Symbols:: $\mathop{\mathrm{erfc}\/}\nolimits z$ : complementary error function, $dx$ : differential of $x$ , $e$ : base of exponential function, $\int$ : integral, $\mathop{\tan\/}\nolimits z$ : tangent function and $\lambda$ : parameter
Referenced by:: Table 3.5.20
Permalink:: http://dlmf.nist.gov/3.5.E45
Encodings:: TeX, pMML, png

The integrand can be extended as a periodic $\mathop{C^{{\infty}}\/}\nolimits$ function on $\Real$ with period $2\pi$ and as noted in §3.5(i), the trapezoidal rule is exceptionally efficient in this case.

Table 3.5.20 gives the results of applying the composite trapezoidal rule (3.5.2) with step size $h$ ; $n$ indicates the number of function values in the rule that are larger than $10^{{-15}}$ (we exploit the fact that the integrand is even). All digits shown in the approximation in the final row are correct.

Table 3.5.20: Composite trapezoidal rule for the integral (3.5.45) with $\lambda=10$ .

$h$	$\mathop{\mathrm{erfc}\/}\nolimits\lambda$		$n$
0.25	0.20949 49432 96679	×10⁻⁴⁴	5
0.20	0.20886 11645 34559	×10⁻⁴⁴	6
0.15	0.20884 87588 72946	×10⁻⁴⁴	8
0.10	0.20884 87583 76254	×10⁻⁴⁴	11

Symbols:: $\mathop{\mathrm{erfc}\/}\nolimits z$ : complementary error function and $\lambda$ : parameter
Keywords:: quadrature
Referenced by:: ¶ ‣ §3.5(ix)
Permalink:: http://dlmf.nist.gov/3.5.T20

A second example is provided in Gil et al. (2001), where the method of contour integration is used to evaluate Scorer functions of complex argument (§9.12). See also Gil et al. (2003b).

If $f$ is meromorphic, with poles near the saddle point, then the foregoing method can be modified. A special case is the rule for Hilbert transforms (§1.14(v)):

3.5.46 $\mathop{\mathcal{H}\/}\nolimits\left(f;x\right)=\frac{1}{\pi}\pvint _{{-\infty}}^{\infty}\frac{f(t)}{t-x}dt,$ $x\in\Real$ ,

Symbols:: $\mathop{\mathcal{H}\/}\nolimits\left(f;x\right)$ : Hilbert transform, $dx$ : differential of $x$ , $\in$ : element of, $\pvint _{a}^{b}$ : Cauchy principal value and $\Real$ : real line (excluding infinity)
Permalink:: http://dlmf.nist.gov/3.5.E46
Encodings:: TeX, pMML, png

where the integral is the Cauchy principal value. See Kress and Martensen (1970).

Other contour integrals occur in standard integral transforms or their inverses, for example, Hankel transforms (§10.22(v)), Kontorovich–Lebedev transforms (§10.43(v)), and Mellin transforms (§1.14(iv)).

§3.5(x) Cubature Formulas

Notes:: For the cubature formulas shown in Table 3.5.21 see Stroud (1971, pp. 243–249) (for the square) and Stroud (1971, pp. 278–279) (for the disk).
Keywords:: Monte-Carlo methods, cubature, weight functions
Permalink:: http://dlmf.nist.gov/3.5.x

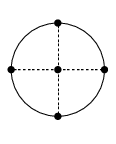
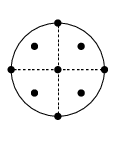
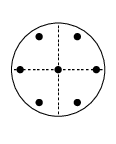
Table 3.5.21 supplies cubature rules, including weights $w_{j}$ , for the disk $D$ , given by $x^{2}+y^{2}\leq h^{2}$ :

3.5.47 $\frac{1}{\pi h^{2}}\iint _{D}f(x,y)dxdy=\sum _{{j=1}}^{n}w_{j}f(x_{j},y_{j})+R,$

Symbols:: $dx$ : differential of $x$ , $(a,b)$ : open interval, $D$ : disk, $R$ : remainder and $w_{k}$ : weights
A&S Ref:: 25.4.61
Permalink:: http://dlmf.nist.gov/3.5.E47
Encodings:: TeX, pMML, png

and the square $S$ , given by $\left|x\right|\leq h$ , $\left|y\right|\leq h$ :

3.5.48 $\frac{1}{4h^{2}}\iint _{S}f(x,y)dxdy=\sum _{{j=1}}^{n}w_{j}f(x_{j},y_{j})+R.$

Symbols:: $dx$ : differential of $x$ , $(a,b)$ : open interval, $R$ : remainder and $w_{k}$ : weights
A&S Ref:: 25.4.62
Permalink:: http://dlmf.nist.gov/3.5.E48
Encodings:: TeX, pMML, png

For these results and further information on cubature formulas see Cools (2003).

For integrals in higher dimensions, Monte Carlo methods are another—often the only—alternative. The standard Monte Carlo method samples points uniformly from the integration region to estimate the integral and its error. In more advanced methods points are sampled from a probability distribution, so that they are concentrated in regions that make the largest contribution to the integral. With $N$ function values, the Monte Carlo method aims at an error of order $1/\sqrt{N}$ , independently of the dimension of the domain of integration. See Davis and Rabinowitz (1984, pp. 384–417) and Schürer (2004).

Table 3.5.21: Cubature formulas for disk and square.

Diagram	$(x_{j},y_{j})$	$w_{j}$	$R$
$\begin{picture}(2.4,3.0)(-1.2,-1.55)\put(0.0,0.0){\line(1,0){0.05}}\put(0.1,0.0){\line(1,0){0.05}}\put(0.2,0.0){\line(1,0){0.05}}\put(0.3,0.0){\line(1,0){0.05}}\put(0.4,0.0){\line(1,0){0.05}}\put(0.5,0.0){\line(1,0){0.05}}\put(0.6,0.0){\line(1,0){0.05}}\put(0.7,0.0){\line(1,0){0.05}}\put(0.8,0.0){\line(1,0){0.05}}\put(0.9,0.0){\line(1,0){0.05}}\put(0.0,0.0){\line(0,1){0.05}}\put(0.0,0.1){\line(0,1){0.05}}\put(0.0,0.2){\line(0,1){0.05}}\put(0.0,0.3){\line(0,1){0.05}}\put(0.0,0.4){\line(0,1){0.05}}\put(0.0,0.5){\line(0,1){0.05}}\put(0.0,0.6){\line(0,1){0.05}}\put(0.0,0.7){\line(0,1){0.05}}\put(0.0,0.8){\line(0,1){0.05}}\put(0.0,0.9){\line(0,1){0.05}}\put(0.0,0.0){\line(-1,0){0.05}}\put(-0.1,0.0){\line(-1,0){0.05}}\put(-0.2,0.0){\line(-1,0){0.05}}\put(-0.3,0.0){\line(-1,0){0.05}}\put(-0.4,0.0){\line(-1,0){0.05}}\put(-0.5,0.0){\line(-1,0){0.05}}\put(-0.6,0.0){\line(-1,0){0.05}}\put(-0.7,0.0){\line(-1,0){0.05}}\put(-0.8,0.0){\line(-1,0){0.05}}\put(-0.9,0.0){\line(-1,0){0.05}}\put(0.0,0.0){\line(0,-1){0.05}}\put(0.0,-0.1){\line(0,-1){0.05}}\put(0.0,-0.2){\line(0,-1){0.05}}\put(0.0,-0.3){\line(0,-1){0.05}}\put(0.0,-0.4){\line(0,-1){0.05}}\put(0.0,-0.5){\line(0,-1){0.05}}\put(0.0,-0.6){\line(0,-1){0.05}}\put(0.0,-0.7){\line(0,-1){0.05}}\put(0.0,-0.8){\line(0,-1){0.05}}\put(0.0,-0.9){\line(0,-1){0.05}}\put(0.0,0.0){\circle{2.0}}\put(0.0,0.0){\circle{0.15}}\put(1.0,0.0){\circle{0.15}}\put(0.0,1.0){\circle{0.15}}\put(-1.0,0.0){\circle{0.15}}\put(0.0,-1.0){\circle*{0.15}}\end{picture}$
	$(0,0)$	$\tfrac{1}{2}$	$\mathop{O\/}\nolimits\!\left(h^{4}\right)$
	$(\pm h,0)$	$\tfrac{1}{8}$
	$(0,\pm h)$	$\tfrac{1}{8}$

$\begin{picture}(2.4,3.0)(-1.2,-1.55)\put(0.0,0.0){\line(1,0){0.05}}\put(0.1,0.0){\line(1,0){0.05}}\put(0.2,0.0){\line(1,0){0.05}}\put(0.3,0.0){\line(1,0){0.05}}\put(0.4,0.0){\line(1,0){0.05}}\put(0.5,0.0){\line(1,0){0.05}}\put(0.6,0.0){\line(1,0){0.05}}\put(0.7,0.0){\line(1,0){0.05}}\put(0.8,0.0){\line(1,0){0.05}}\put(0.9,0.0){\line(1,0){0.05}}\put(0.0,0.0){\line(0,1){0.05}}\put(0.0,0.1){\line(0,1){0.05}}\put(0.0,0.2){\line(0,1){0.05}}\put(0.0,0.3){\line(0,1){0.05}}\put(0.0,0.4){\line(0,1){0.05}}\put(0.0,0.5){\line(0,1){0.05}}\put(0.0,0.6){\line(0,1){0.05}}\put(0.0,0.7){\line(0,1){0.05}}\put(0.0,0.8){\line(0,1){0.05}}\put(0.0,0.9){\line(0,1){0.05}}\put(0.0,0.0){\line(-1,0){0.05}}\put(-0.1,0.0){\line(-1,0){0.05}}\put(-0.2,0.0){\line(-1,0){0.05}}\put(-0.3,0.0){\line(-1,0){0.05}}\put(-0.4,0.0){\line(-1,0){0.05}}\put(-0.5,0.0){\line(-1,0){0.05}}\put(-0.6,0.0){\line(-1,0){0.05}}\put(-0.7,0.0){\line(-1,0){0.05}}\put(-0.8,0.0){\line(-1,0){0.05}}\put(-0.9,0.0){\line(-1,0){0.05}}\put(0.0,0.0){\line(0,-1){0.05}}\put(0.0,-0.1){\line(0,-1){0.05}}\put(0.0,-0.2){\line(0,-1){0.05}}\put(0.0,-0.3){\line(0,-1){0.05}}\put(0.0,-0.4){\line(0,-1){0.05}}\put(0.0,-0.5){\line(0,-1){0.05}}\put(0.0,-0.6){\line(0,-1){0.05}}\put(0.0,-0.7){\line(0,-1){0.05}}\put(0.0,-0.8){\line(0,-1){0.05}}\put(0.0,-0.9){\line(0,-1){0.05}}\put(0.0,0.0){\circle{2.0}}\put(0.5,0.5){\circle{0.15}}\put(-0.5,0.5){\circle{0.15}}\put(0.5,-0.5){\circle{0.15}}\put(-0.5,-0.5){\circle{0.15}}\end{picture}$

	$(\pm\tfrac{1}{2}h,\pm\tfrac{1}{2}h)$	$\tfrac{1}{4}$	$\mathop{O\/}\nolimits\!\left(h^{4}\right)$


$\begin{picture}(2.4,3.0)(-1.2,-1.55)\put(0.0,0.0){\line(1,0){0.05}}\put(0.1,0.0){\line(1,0){0.05}}\put(0.2,0.0){\line(1,0){0.05}}\put(0.3,0.0){\line(1,0){0.05}}\put(0.4,0.0){\line(1,0){0.05}}\put(0.5,0.0){\line(1,0){0.05}}\put(0.6,0.0){\line(1,0){0.05}}\put(0.7,0.0){\line(1,0){0.05}}\put(0.8,0.0){\line(1,0){0.05}}\put(0.9,0.0){\line(1,0){0.05}}\put(0.0,0.0){\line(0,1){0.05}}\put(0.0,0.1){\line(0,1){0.05}}\put(0.0,0.2){\line(0,1){0.05}}\put(0.0,0.3){\line(0,1){0.05}}\put(0.0,0.4){\line(0,1){0.05}}\put(0.0,0.5){\line(0,1){0.05}}\put(0.0,0.6){\line(0,1){0.05}}\put(0.0,0.7){\line(0,1){0.05}}\put(0.0,0.8){\line(0,1){0.05}}\put(0.0,0.9){\line(0,1){0.05}}\put(0.0,0.0){\line(-1,0){0.05}}\put(-0.1,0.0){\line(-1,0){0.05}}\put(-0.2,0.0){\line(-1,0){0.05}}\put(-0.3,0.0){\line(-1,0){0.05}}\put(-0.4,0.0){\line(-1,0){0.05}}\put(-0.5,0.0){\line(-1,0){0.05}}\put(-0.6,0.0){\line(-1,0){0.05}}\put(-0.7,0.0){\line(-1,0){0.05}}\put(-0.8,0.0){\line(-1,0){0.05}}\put(-0.9,0.0){\line(-1,0){0.05}}\put(0.0,0.0){\line(0,-1){0.05}}\put(0.0,-0.1){\line(0,-1){0.05}}\put(0.0,-0.2){\line(0,-1){0.05}}\put(0.0,-0.3){\line(0,-1){0.05}}\put(0.0,-0.4){\line(0,-1){0.05}}\put(0.0,-0.5){\line(0,-1){0.05}}\put(0.0,-0.6){\line(0,-1){0.05}}\put(0.0,-0.7){\line(0,-1){0.05}}\put(0.0,-0.8){\line(0,-1){0.05}}\put(0.0,-0.9){\line(0,-1){0.05}}\put(0.0,0.0){\circle{2.0}}\put(0.0,0.0){\circle{0.15}}\put(-1.0,0.0){\circle{0.15}}\put(1.0,0.0){\circle{0.15}}\put(0.0,-1.0){\circle{0.15}}\put(0.0,1.0){\circle{0.15}}\put(0.5,0.5){\circle{0.15}}\put(-0.5,0.5){\circle{0.15}}\put(0.5,-0.5){\circle{0.15}}\put(-0.5,-0.5){\circle*{0.15}}\end{picture}$
	$(0,0)$	$\tfrac{1}{6}$	$\mathop{O\/}\nolimits\!\left(h^{6}\right)$
	$(\pm h,0)$ , $(0,\pm h)$	$\tfrac{1}{24}$
	$(\pm\tfrac{1}{2}h,\pm\tfrac{1}{2}h)$	$\tfrac{1}{6}$

$\begin{picture}(2.4,3.0)(-1.2,-1.55)\put(0.0,0.0){\line(1,0){0.05}}\put(0.1,0.0){\line(1,0){0.05}}\put(0.2,0.0){\line(1,0){0.05}}\put(0.3,0.0){\line(1,0){0.05}}\put(0.4,0.0){\line(1,0){0.05}}\put(0.5,0.0){\line(1,0){0.05}}\put(0.6,0.0){\line(1,0){0.05}}\put(0.7,0.0){\line(1,0){0.05}}\put(0.8,0.0){\line(1,0){0.05}}\put(0.9,0.0){\line(1,0){0.05}}\put(0.0,0.0){\line(0,1){0.05}}\put(0.0,0.1){\line(0,1){0.05}}\put(0.0,0.2){\line(0,1){0.05}}\put(0.0,0.3){\line(0,1){0.05}}\put(0.0,0.4){\line(0,1){0.05}}\put(0.0,0.5){\line(0,1){0.05}}\put(0.0,0.6){\line(0,1){0.05}}\put(0.0,0.7){\line(0,1){0.05}}\put(0.0,0.8){\line(0,1){0.05}}\put(0.0,0.9){\line(0,1){0.05}}\put(0.0,0.0){\line(-1,0){0.05}}\put(-0.1,0.0){\line(-1,0){0.05}}\put(-0.2,0.0){\line(-1,0){0.05}}\put(-0.3,0.0){\line(-1,0){0.05}}\put(-0.4,0.0){\line(-1,0){0.05}}\put(-0.5,0.0){\line(-1,0){0.05}}\put(-0.6,0.0){\line(-1,0){0.05}}\put(-0.7,0.0){\line(-1,0){0.05}}\put(-0.8,0.0){\line(-1,0){0.05}}\put(-0.9,0.0){\line(-1,0){0.05}}\put(0.0,0.0){\line(0,-1){0.05}}\put(0.0,-0.1){\line(0,-1){0.05}}\put(0.0,-0.2){\line(0,-1){0.05}}\put(0.0,-0.3){\line(0,-1){0.05}}\put(0.0,-0.4){\line(0,-1){0.05}}\put(0.0,-0.5){\line(0,-1){0.05}}\put(0.0,-0.6){\line(0,-1){0.05}}\put(0.0,-0.7){\line(0,-1){0.05}}\put(0.0,-0.8){\line(0,-1){0.05}}\put(0.0,-0.9){\line(0,-1){0.05}}\put(0.0,0.0){\circle{2.0}}\put(0.0,0.0){\circle{0.15}}\put(0.8165,0.0){\circle{0.15}}\put(-0.8165,0.0){\circle{0.15}}\put(0.408,0.707){\circle{0.15}}\put(-0.408,0.707){\circle{0.15}}\put(0.408,-0.707){\circle{0.15}}\put(-0.408,-0.707){\circle*{0.15}}\end{picture}$
	$(0,0)$	$\tfrac{1}{4}$	$\mathop{O\/}\nolimits\!\left(h^{6}\right)$
	$(\pm\tfrac{1}{3}\sqrt{6}h,0)$	$\tfrac{1}{8}$
	$(\pm\tfrac{1}{6}\sqrt{6}h,\pm\tfrac{1}{2}\sqrt{2}h)$	$\tfrac{1}{8}$

$\begin{picture}(2.4,3.0)(-1.2,-1.55)\put(0.0,0.0){\line(1,0){0.05}}\put(0.1,0.0){\line(1,0){0.05}}\put(0.2,0.0){\line(1,0){0.05}}\put(0.3,0.0){\line(1,0){0.05}}\put(0.4,0.0){\line(1,0){0.05}}\put(0.5,0.0){\line(1,0){0.05}}\put(0.6,0.0){\line(1,0){0.05}}\put(0.7,0.0){\line(1,0){0.05}}\put(0.8,0.0){\line(1,0){0.05}}\put(0.9,0.0){\line(1,0){0.05}}\put(0.0,0.0){\line(0,1){0.05}}\put(0.0,0.1){\line(0,1){0.05}}\put(0.0,0.2){\line(0,1){0.05}}\put(0.0,0.3){\line(0,1){0.05}}\put(0.0,0.4){\line(0,1){0.05}}\put(0.0,0.5){\line(0,1){0.05}}\put(0.0,0.6){\line(0,1){0.05}}\put(0.0,0.7){\line(0,1){0.05}}\put(0.0,0.8){\line(0,1){0.05}}\put(0.0,0.9){\line(0,1){0.05}}\put(0.0,0.0){\line(-1,0){0.05}}\put(-0.1,0.0){\line(-1,0){0.05}}\put(-0.2,0.0){\line(-1,0){0.05}}\put(-0.3,0.0){\line(-1,0){0.05}}\put(-0.4,0.0){\line(-1,0){0.05}}\put(-0.5,0.0){\line(-1,0){0.05}}\put(-0.6,0.0){\line(-1,0){0.05}}\put(-0.7,0.0){\line(-1,0){0.05}}\put(-0.8,0.0){\line(-1,0){0.05}}\put(-0.9,0.0){\line(-1,0){0.05}}\put(0.0,0.0){\line(0,-1){0.05}}\put(0.0,-0.1){\line(0,-1){0.05}}\put(0.0,-0.2){\line(0,-1){0.05}}\put(0.0,-0.3){\line(0,-1){0.05}}\put(0.0,-0.4){\line(0,-1){0.05}}\put(0.0,-0.5){\line(0,-1){0.05}}\put(0.0,-0.6){\line(0,-1){0.05}}\put(0.0,-0.7){\line(0,-1){0.05}}\put(0.0,-0.8){\line(0,-1){0.05}}\put(0.0,-0.9){\line(0,-1){0.05}}\put(-1.0,1.0){\line(1,0){2.0}}\put(-1.0,1.0){\line(0,-1){2.0}}\put(1.0,-1.0){\line(-1,0){2.0}}\put(1.0,-1.0){\line(0,1){2.0}}\put(0.0,0.0){\circle{0.15}}\put(1.0,0.0){\circle{0.15}}\put(-1.0,0.0){\circle{0.15}}\put(0.0,1.0){\circle{0.15}}\put(0.0,-1.0){\circle{0.15}}\put(1.0,1.0){\circle{0.15}}\put(-1.0,1.0){\circle{0.15}}\put(1.0,-1.0){\circle{0.15}}\put(-1.0,-1.0){\circle*{0.15}}\end{picture}$
	$(0,0)$	$\tfrac{4}{9}$	$\mathop{O\/}\nolimits\!\left(h^{4}\right)$
	$(\pm h,0)$ , $(0,\pm h)$	$\tfrac{1}{9}$
	$(\pm h,\pm h)$	$\tfrac{1}{36}$

$\begin{picture}(2.4,3.0)(-1.2,-1.55)\put(0.0,0.0){\line(1,0){0.05}}\put(0.1,0.0){\line(1,0){0.05}}\put(0.2,0.0){\line(1,0){0.05}}\put(0.3,0.0){\line(1,0){0.05}}\put(0.4,0.0){\line(1,0){0.05}}\put(0.5,0.0){\line(1,0){0.05}}\put(0.6,0.0){\line(1,0){0.05}}\put(0.7,0.0){\line(1,0){0.05}}\put(0.8,0.0){\line(1,0){0.05}}\put(0.9,0.0){\line(1,0){0.05}}\put(0.0,0.0){\line(0,1){0.05}}\put(0.0,0.1){\line(0,1){0.05}}\put(0.0,0.2){\line(0,1){0.05}}\put(0.0,0.3){\line(0,1){0.05}}\put(0.0,0.4){\line(0,1){0.05}}\put(0.0,0.5){\line(0,1){0.05}}\put(0.0,0.6){\line(0,1){0.05}}\put(0.0,0.7){\line(0,1){0.05}}\put(0.0,0.8){\line(0,1){0.05}}\put(0.0,0.9){\line(0,1){0.05}}\put(0.0,0.0){\line(-1,0){0.05}}\put(-0.1,0.0){\line(-1,0){0.05}}\put(-0.2,0.0){\line(-1,0){0.05}}\put(-0.3,0.0){\line(-1,0){0.05}}\put(-0.4,0.0){\line(-1,0){0.05}}\put(-0.5,0.0){\line(-1,0){0.05}}\put(-0.6,0.0){\line(-1,0){0.05}}\put(-0.7,0.0){\line(-1,0){0.05}}\put(-0.8,0.0){\line(-1,0){0.05}}\put(-0.9,0.0){\line(-1,0){0.05}}\put(0.0,0.0){\line(0,-1){0.05}}\put(0.0,-0.1){\line(0,-1){0.05}}\put(0.0,-0.2){\line(0,-1){0.05}}\put(0.0,-0.3){\line(0,-1){0.05}}\put(0.0,-0.4){\line(0,-1){0.05}}\put(0.0,-0.5){\line(0,-1){0.05}}\put(0.0,-0.6){\line(0,-1){0.05}}\put(0.0,-0.7){\line(0,-1){0.05}}\put(0.0,-0.8){\line(0,-1){0.05}}\put(0.0,-0.9){\line(0,-1){0.05}}\put(-1.0,1.0){\line(1,0){2.0}}\put(-1.0,1.0){\line(0,-1){2.0}}\put(1.0,-1.0){\line(-1,0){2.0}}\put(1.0,-1.0){\line(0,1){2.0}}\put(0.577,0.577){\circle{0.15}}\put(-0.577,0.577){\circle{0.15}}\put(0.577,-0.577){\circle{0.15}}\put(-0.577,-0.577){\circle{0.15}}\end{picture}$

	$(\pm\tfrac{1}{3}\sqrt{3}h,\pm\tfrac{1}{3}\sqrt{3}h)$	$\tfrac{1}{4}$	$\mathop{O\/}\nolimits\!\left(h^{4}\right)$


$\begin{picture}(2.4,3.0)(-1.2,-1.55)\put(0.0,0.0){\line(1,0){0.05}}\put(0.1,0.0){\line(1,0){0.05}}\put(0.2,0.0){\line(1,0){0.05}}\put(0.3,0.0){\line(1,0){0.05}}\put(0.4,0.0){\line(1,0){0.05}}\put(0.5,0.0){\line(1,0){0.05}}\put(0.6,0.0){\line(1,0){0.05}}\put(0.7,0.0){\line(1,0){0.05}}\put(0.8,0.0){\line(1,0){0.05}}\put(0.9,0.0){\line(1,0){0.05}}\put(0.0,0.0){\line(0,1){0.05}}\put(0.0,0.1){\line(0,1){0.05}}\put(0.0,0.2){\line(0,1){0.05}}\put(0.0,0.3){\line(0,1){0.05}}\put(0.0,0.4){\line(0,1){0.05}}\put(0.0,0.5){\line(0,1){0.05}}\put(0.0,0.6){\line(0,1){0.05}}\put(0.0,0.7){\line(0,1){0.05}}\put(0.0,0.8){\line(0,1){0.05}}\put(0.0,0.9){\line(0,1){0.05}}\put(0.0,0.0){\line(-1,0){0.05}}\put(-0.1,0.0){\line(-1,0){0.05}}\put(-0.2,0.0){\line(-1,0){0.05}}\put(-0.3,0.0){\line(-1,0){0.05}}\put(-0.4,0.0){\line(-1,0){0.05}}\put(-0.5,0.0){\line(-1,0){0.05}}\put(-0.6,0.0){\line(-1,0){0.05}}\put(-0.7,0.0){\line(-1,0){0.05}}\put(-0.8,0.0){\line(-1,0){0.05}}\put(-0.9,0.0){\line(-1,0){0.05}}\put(0.0,0.0){\line(0,-1){0.05}}\put(0.0,-0.1){\line(0,-1){0.05}}\put(0.0,-0.2){\line(0,-1){0.05}}\put(0.0,-0.3){\line(0,-1){0.05}}\put(0.0,-0.4){\line(0,-1){0.05}}\put(0.0,-0.5){\line(0,-1){0.05}}\put(0.0,-0.6){\line(0,-1){0.05}}\put(0.0,-0.7){\line(0,-1){0.05}}\put(0.0,-0.8){\line(0,-1){0.05}}\put(0.0,-0.9){\line(0,-1){0.05}}\put(-1.0,1.0){\line(1,0){2.0}}\put(-1.0,1.0){\line(0,-1){2.0}}\put(1.0,-1.0){\line(-1,0){2.0}}\put(1.0,-1.0){\line(0,1){2.0}}\put(0.0,0.0){\circle{0.15}}\put(0.7746,0.0){\circle{0.15}}\put(-0.7746,0.0){\circle{0.15}}\put(0.0,0.7746){\circle{0.15}}\put(0.0,-0.7746){\circle{0.15}}\put(0.7746,0.7746){\circle{0.15}}\put(-0.7746,0.7746){\circle{0.15}}\put(0.7746,-0.7746){\circle{0.15}}\put(-0.7746,-0.7746){\circle*{0.15}}\end{picture}$
	$(0,0)$	$\tfrac{16}{81}$	$\mathop{O\/}\nolimits\!\left(h^{6}\right)$
	$(\pm\sqrt{\tfrac{3}{5}}h,0)$ , $(0,\pm\sqrt{\tfrac{3}{5}}h)$	$\tfrac{10}{81}$
	$(\pm\sqrt{\tfrac{3}{5}}h,0)$ , $(\pm\sqrt{\tfrac{3}{5}}h,0)$	$\tfrac{25}{324}$