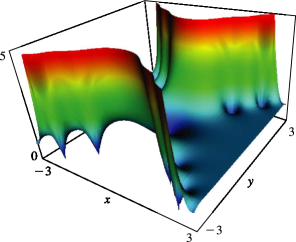
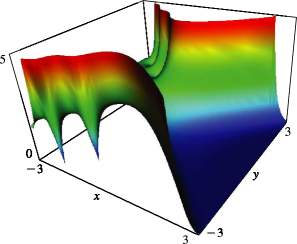
error functions
(0.008 seconds)
1—10 of 171 matching pages
1: 7.18 Repeated Integrals of the Complementary Error Function
2: 7.2 Definitions
§7.2(i) Error Functions
… ►Values at Infinity
►3: 7.25 Software
4: 7.10 Derivatives
5: 7.24 Approximations
Hastings (1955) gives several minimax polynomial and rational approximations for , and the auxiliary functions and .
Cody (1969) provides minimax rational approximations for and . The maximum relative precision is about 20S.
Schonfelder (1978) gives coefficients of Chebyshev expansions for on , for on , and for on (30D).
Shepherd and Laframboise (1981) gives coefficients of Chebyshev series for on (22D).
Luke (1969b, vol. 2, pp. 422–435) gives main diagonal Padé approximations for , , , , and ; approximate errors are given for a selection of -values.
6: 7.1 Special Notation
7: 7.21 Physical Applications
§7.21 Physical Applications
►The error functions, Fresnel integrals, and related functions occur in a variety of physical applications. … ►Carslaw and Jaeger (1959) gives many applications and points out the importance of the repeated integrals of the complementary error function . Fried and Conte (1961) mentions the role of in the theory of linearized waves or oscillations in a hot plasma; is called the plasma dispersion function or Faddeeva (or Faddeyeva) function; see Faddeeva and Terent’ev (1954). … ►8: 7.3 Graphics
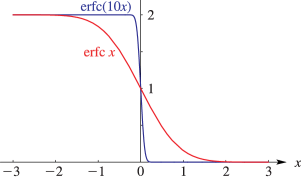 ►
►
9: 7.17 Inverse Error Functions
§7.17 Inverse Error Functions
… ►The inverses of the functions , , , are denoted by ►§7.17(iii) Asymptotic Expansion of for Small
…10: 7.23 Tables
Abramowitz and Stegun (1964, Chapter 7) includes , , , 10D; , , 8S; , , 7D; , , , 6S; , , 10D; , , 9D; , , , 7D; , , , , 15D.
Zhang and Jin (1996, pp. 637, 639) includes , , , 8D; , , , 8D.
Abramowitz and Stegun (1964, Chapter 7) includes , , , 6D.
Fettis et al. (1973) gives the first 100 zeros of and (the table on page 406 of this reference is for , not for ), 11S.
Zhang and Jin (1996, p. 642) includes the first 10 zeros of , 9D; the first 25 distinct zeros of and , 8S.