Digital Library of Mathematical Functions
About the Project
NIST
2 Asymptotic ApproximationsAreas

§2.10 Sums and Sequences

Contents

§2.10(i) Euler–Maclaurin Formula

As in §24.2, let \mathop{B_{{n}}\/}\nolimits and \mathop{B_{{n}}\/}\nolimits\!\left(x\right) denote the nth Bernoulli number and polynomial, respectively, and \mathop{\widetilde{B}_{{n}}\/}\nolimits\!\left(x\right) the nth Bernoulli periodic function \mathop{B_{{n}}\/}\nolimits\!\left(x-\left\lfloor x\right\rfloor\right).

Assume that a,m, and n are integers such that n>a, m>0, and f^{{(2m)}}(x) is absolutely integrable over [a,n]. Then

This is the Euler–Maclaurin formula. Another version is the Abel–Plana formula:

\vartheta_{n} being some number in the interval (0,1). Sufficient conditions for the validity of this second result are:

  1. (a)

    On the strip a\leq\realpart{z}\leq n, f(z) is analytic in its interior, f^{{(2m)}}(z) is continuous on its closure, and f(z)=\mathop{o\/}\nolimits\!\left(e^{{2\pi|\imagpart{z}|}}\right) as \imagpart{z}\to\pm\infty, uniformly with respect to \realpart{z}\in[a,n].

  2. (b)

    f(z) is real when a\leq z\leq n.

  3. (c)

    The first infinite integral in (2.10.2) converges.

Example

for large n. From (2.10.1)

where m (\geq 2) is arbitrary, C is a constant, and

From §24.12(i), (24.2.2), and (24.4.27), \mathop{\widetilde{B}_{{2m}}\/}\nolimits\!\left(x\right)-\mathop{B_{{2m}}\/}\nolimits is of constant sign (-1)^{m}. Thus R_{m}(n) and R_{{m+1}}(n) are of opposite signs, and since their difference is the term corresponding to s=m in (2.10.4), R_{m}(n) is bounded in absolute value by this term and has the same sign.

Formula (2.10.2) is useful for evaluating the constant term in expansions obtained from (2.10.1). In the present example it leads to

where \EulerConstant is Euler’s constant (§5.2(ii)) and {\mathop{\zeta\/}\nolimits^{{\prime}}} is the derivative of the Riemann zeta function (§25.2(i)). e^{C} is sometimes called Glaisher’s constant. For further information on C see §5.17.

Other examples that can be verified in a similar way are:

where \alpha (\neq-1) is a real constant, and

In both expansions the remainder term is bounded in absolute value by the first neglected term in the sum, and has the same sign, provided that in the case of (2.10.7), truncation takes place at s=2m-1, where m is any positive integer satisfying m\geq\frac{1}{2}(\alpha+1).

For extensions of the Euler–Maclaurin formula to functions f(x) with singularities at x=a or x=n (or both) see Sidi (2004). See also Weniger (2007).

For an extension to integrals with Cauchy principal values see Elliott (1998).

§2.10(ii) Summation by Parts

The formula for summation by parts is

2.10.9\sum_{{j=1}}^{{n-1}}u_{j}v_{j}=U_{{n-1}}v_{n}+\sum_{{j=1}}^{{n-1}}U_{j}(v_{j}-% v_{{j+1}}),
Show Annotations
Symbols:
U_{j}: coefficients, u_{j}: terms and v_{j}: terms
Permalink:
http://dlmf.nist.gov/2.10.E9
Encodings:
TeX, pMML, png

where

2.10.10U_{j}=u_{1}+u_{2}+\dots+u_{j}.
Show Annotations
Symbols:
U_{j}: coefficients and u_{j}: terms
Permalink:
http://dlmf.nist.gov/2.10.E10
Encodings:
TeX, pMML, png

This identity can be used to find asymptotic approximations for large n when the factor v_{j} changes slowly with j, and u_{j} is oscillatory; compare the approximation of Fourier integrals by integration by parts in §2.3(i).

Example

2.10.11S(\alpha,\beta,n)=\sum_{{j=1}}^{{n-1}}e^{{ij\beta}}j^{{\alpha}},

where \alpha and \beta are real constants with e^{{i\beta}}\neq 1.

As a first estimate for large n

according as \alpha<-1, \alpha=-1, or \alpha>-1; see (2.10.7), (2.10.8). With u_{j}=e^{{ij\beta}}, v_{j}=j^{{\alpha}},

and

2.10.14S(\alpha,\beta,n)=\frac{e^{{i\beta}}}{e^{{i\beta}}-1}\left(e^{{i(n-1)\beta}}n^% {{\alpha}}-1+\sum_{{j=1}}^{{n-1}}e^{{ij\beta}}\left(j^{{\alpha}}-(j+1)^{{% \alpha}}\right)\right).

Since

2.10.15j^{{\alpha}}-(j+1)^{{\alpha}}=-\alpha j^{{\alpha-1}}+\alpha(\alpha-1)\mathop{O% \/}\nolimits\!\left(j^{{\alpha-2}}\right)

for any real constant \alpha and the set of all positive integers j, we derive

From this result and (2.10.12)

2.10.17S(\alpha,\beta,n)=\mathop{O\/}\nolimits\!\left(n^{{\alpha}}\right)+\mathop{O\/% }\nolimits\!\left(1\right).
Show Annotations
Symbols:
\mathop{O\/}\nolimits\!\left(x\right): order not exceeding and S(\alpha,\beta,n): sum
Permalink:
http://dlmf.nist.gov/2.10.E17
Encodings:
TeX, pMML, png

Then replacing \alpha by \alpha-1 and resubstituting in (2.10.16), we have

which is a useful approximation when \alpha>0.

For extensions to \alpha\leq 0, higher terms, and other examples, see Olver (1997b, Chapter 8).

§2.10(iii) Asymptotic Expansions of Entire Functions

The asymptotic behavior of entire functions defined by Maclaurin series can be approached by converting the sum into a contour integral by use of the residue theorem and applying the methods of §§2.4 and 2.5.

Example

From §§16.2(i)–16.2(ii)

We seek the behavior as x\to+\infty. From (1.10.8)

where \mathscr{C} comprises the two semicircles and two parts of the imaginary axis depicted in Figure 2.10.1.

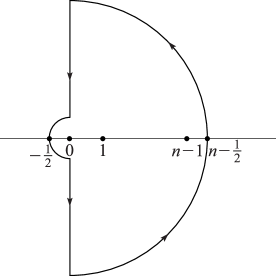
See accompanying text
Figure 2.10.1: t-plane. Contour \mathscr{C}. Magnify
Show Annotations
Symbols:
\mathscr{C}: contour
Referenced by:
‣ §2.10(iii)
Permalink:
http://dlmf.nist.gov/2.10.F1
Encodings:
pdf, png

From the identities

and Cauchy’s theorem, we have

where \mathscr{C}_{1},\mathscr{C}_{2} denote respectively the upper and lower halves of \mathscr{C}. (5.11.7) shows that the integrals around the large quarter circles vanish as n\to\infty. Hence

the last step following from |x^{t}|\leq 1 when t is on the interval [-\frac{1}{2},0], the imaginary axis, or the small semicircle. By application of Laplace’s method (§2.3(iii)) and use again of (5.11.7), we obtain

For generalizations and other examples see Olver (1997b, Chapter 8), Ford (1960), and Berndt and Evans (1984). See also Paris and Kaminski (2001, Chapter 5) and §§16.11(i)–16.11(ii).

§2.10(iv) Taylor and Laurent Coefficients: Darboux’s Method

Let f(z) be analytic on the annulus 0<|z|<r, with Laurent expansion

What is the asymptotic behavior of f_{n} as n\to\infty or n\to-\infty? More specially, what is the behavior of the higher coefficients in a Taylor-series expansion?

These problems can be brought within the scope of §2.4 by means of Cauchy’s integral formula

where \mathscr{C} is a simple closed contour in the annulus that encloses z=0. For examples see Olver (1997b, Chapters 8, 9).

However, if r is finite and f(z) has algebraic or logarithmic singularities on |z|=r, then Darboux’s method is usually easier to apply. We need a “comparison function” g(z) with the properties:

  1. (a)

    g(z) is analytic on 0<|z|<r.

  2. (b)

    f(z)-g(z) is continuous on 0<|z|\leq r.

  3. (c)

    The coefficients in the Laurent expansion

    have known asymptotic behavior as n\to\pm\infty.

By allowing the contour in Cauchy’s formula to expand, we find that

Hence by the Riemann–Lebesgue lemma (§1.8(i))

This result is refinable in two important ways. First, the conditions can be weakened. It is unnecessary for f(z)-g(z) to be continuous on |z|=r: it suffices that the integrals in (2.10.28) converge uniformly. For example, Condition (b) can be replaced by:

  1. (b´)

    On the circle |z|=r, the function f(z)-g(z) has a finite number of singularities, and at each singularity z_{j}, say,

    where \sigma_{j} is a positive constant.

Secondly, when f(z)-g(z) is m times continuously differentiable on |z|=r the result (2.10.29) can be strengthened. In these circumstances the integrals in (2.10.28) are integrable by parts m times, yielding

Furthermore, (2.10.31) remains valid with the weaker condition

in the neighborhood of each singularity z_{j}, again with \sigma_{j}>0.

Example

Let \alpha be a constant in (0,2\pi) and \mathop{P_{{n}}\/}\nolimits denote the Legendre polynomial of degree n. From §14.7(iv)

The singularities of f(z) on the unit circle are branch points at z=e^{{\pm i\alpha}}. To match the limiting behavior of f(z) at these points we set

Here the branch of \left(e^{{-i\alpha}}-z\right)^{{-1/2}} is continuous in the z-plane cut along the outward-drawn ray through z=e^{{-i\alpha}} and equals e^{{i\alpha/2}} at z=0. Similarly for \left(e^{{i\alpha}}-z\right)^{{-1/2}}. In Condition (c) we have

and in the supplementary conditions we may set m=1. Then from (2.10.31) and (5.11.7)

For higher terms see §18.15(iii).

For uniform expansions when two singularities coalesce on the circle of convergence see Wong and Zhao (2005).

For other examples and extensions see Olver (1997b, Chapter 8), Olver (1970), Wong (1989, Chapter 2), and Wong and Wyman (1974). See also Flajolet and Odlyzko (1990).

© 2010–2013 NIST / Privacy Policy / Disclaimer / Feedback; Version 1.0.6; Release date 2013-05-06 Math-Image version (See MathML) . A Printed Companionis available.