§4.2 Definitions

Referenced by:: §1.7(iv)
Permalink:: http://dlmf.nist.gov/4.2

§4.2(i) The Logarithm
§4.2(ii) Logarithms to a General Base $a$
§4.2(iii) The Exponential Function
§4.2(iv) Powers

§4.2(i) The Logarithm

Notes:: See Levinson and Redheffer (1970, pp. 62–65).
Keywords:: branch, branch cut, logarithm function, multivalued function, principal values
Referenced by:: ¶ ‣ §1.10(i), ¶ ‣ §1.4(iv), ¶ ‣ §1.9(vi), ¶ ‣ §10.2(ii), §10.43(iv), §11.2(i), ¶ ‣ §13.14(i), ¶ ‣ §13.2(i), §13.9(i), §14.1, §14.21(i), §15.2(i), §16.2(iii), §25.12(i), §30.6, §33.7, §4.23(ii), §4.37(ii), §5.17, §6.2(i), §8.2(i), §8.21(ii), Methodology
Permalink:: http://dlmf.nist.gov/4.2.i

The general logarithm function $\mathop{\mathrm{Ln}\/}\nolimits z$ is defined by

4.2.1 $\mathop{\mathrm{Ln}\/}\nolimits z=\int _{1}^{z}\frac{dt}{t},$ $z\neq 0$ ,

Defines:: $\mathop{\mathrm{Ln}\/}\nolimits z$ : general logarithm function
Symbols:: $dx$ : differential of $x$ , $\int$ : integral and $z$ : complex variable
A&S Ref:: 4.1.4
Referenced by:: §4.2(i)
Permalink:: http://dlmf.nist.gov/4.2.E1
Encodings:: TeX, pMML, png

where the integration path does not intersect the origin. This is a multivalued function of $z$ with branch point at $z=0$ .

The principal value, or principal branch, is defined by

4.2.2 $\mathop{\ln\/}\nolimits z=\int _{1}^{z}\frac{dt}{t},$

Defines:: $\mathop{\ln\/}\nolimits z$ : principal branch of logarithm function
Symbols:: $dx$ : differential of $x$ , $\int$ : integral and $z$ : complex variable
A&S Ref:: 4.1.1
Permalink:: http://dlmf.nist.gov/4.2.E2
Encodings:: TeX, pMML, png

where the path does not intersect $(-\infty,0]$ ; see Figure 4.2.1. $\mathop{\ln\/}\nolimits z$ is a single-valued analytic function on $\Complex\setminus(-\infty,0]$ and real-valued when $z$ ranges over the positive real numbers.

Figure 4.2.1: $z$ -plane: Branch cut for $\mathop{\ln\/}\nolimits z$ and $z^{\alpha}$ .

Symbols:: $\mathop{\ln\/}\nolimits z$ : principal branch of logarithm function and $z$ : complex variable
Keywords:: branch cut, logarithm function, power function
Referenced by:: ¶ ‣ §4.2(iv), §4.2(i), §4.2(i)
Permalink:: http://dlmf.nist.gov/4.2.F1
Encodings:: pdf, png

The real and imaginary parts of $\mathop{\ln\/}\nolimits z$ are given by

4.2.3 $\mathop{\ln\/}\nolimits z=\mathop{\ln\/}\nolimits\left|z\right|+i\mathop{\mathrm{ph}\/}\nolimits z,$ $-\pi<\mathop{\mathrm{ph}\/}\nolimits z<\pi$ .

Symbols:: $\mathop{\ln\/}\nolimits z$ : principal branch of logarithm function, $\mathop{\mathrm{ph}\/}\nolimits$ : phase and $z$ : complex variable
A&S Ref:: 4.1.2
Referenced by:: §4.2(i)
Permalink:: http://dlmf.nist.gov/4.2.E3
Encodings:: TeX, pMML, png

For $\mathop{\mathrm{ph}\/}\nolimits z$ see §1.9(i).

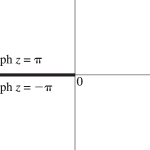
The only zero of $\mathop{\ln\/}\nolimits z$ is at $z=1$ .

Most texts extend the definition of the principal value to include the branch cut

4.2.4 $z=x,$ $-\infty<x<0$ ,

Symbols:: $x$ : real variable and $z$ : complex variable
Permalink:: http://dlmf.nist.gov/4.2.E4
Encodings:: TeX, pMML, png

by replacing (4.2.3) with

4.2.5 $\mathop{\ln\/}\nolimits z=\mathop{\ln\/}\nolimits\left|z\right|+i\mathop{\mathrm{ph}\/}\nolimits z,$ $-\pi<\mathop{\mathrm{ph}\/}\nolimits z\leq\pi$ .

Symbols:: $\mathop{\ln\/}\nolimits z$ : principal branch of logarithm function, $\mathop{\mathrm{ph}\/}\nolimits$ : phase and $z$ : complex variable
Referenced by:: §4.2(i)
Permalink:: http://dlmf.nist.gov/4.2.E5
Encodings:: TeX, pMML, png

With this definition the general logarithm is given by

4.2.6 $\mathop{\mathrm{Ln}\/}\nolimits z=\mathop{\ln\/}\nolimits z+2k\pi i,$

Symbols:: $\mathop{\mathrm{Ln}\/}\nolimits z$ : general logarithm function, $\mathop{\ln\/}\nolimits z$ : principal branch of logarithm function, $k$ : integer and $z$ : complex variable
Referenced by:: §6.4
Permalink:: http://dlmf.nist.gov/4.2.E6
Encodings:: TeX, pMML, png

where $k$ is the excess of the number of times the path in (4.2.1) crosses the negative real axis in the positive sense over the number of times in the negative sense.

In the DLMF we allow a further extension by regarding the cut as representing two sets of points, one set corresponding to the “upper side” and denoted by $z=x+i0$ , the other set corresponding to the “lower side” and denoted by $z=x-i0$ . Again see Figure 4.2.1. Then

4.2.7 $\mathop{\ln\/}\nolimits\!\left(x\pm i0\right)=\mathop{\ln\/}\nolimits|x|\pm i\pi,$ $-\infty<x<0$ ,

Symbols:: $\mathop{\ln\/}\nolimits z$ : principal branch of logarithm function and $x$ : real variable
Permalink:: http://dlmf.nist.gov/4.2.E7
Encodings:: TeX, pMML, png

with either upper signs or lower signs taken throughout. Consequently $\mathop{\ln\/}\nolimits z$ is two-valued on the cut, and discontinuous across the cut. We regard this as the closed definition of the principal value.

In contrast to (4.2.5) the closed definition is symmetric. As a consequence, it has the advantage of extending regions of validity of properties of principal values. For example, with the definition (4.2.5) the identity (4.8.7) is valid only when $\left|\mathop{\mathrm{ph}\/}\nolimits z\right|<\pi$ , but with the closed definition the identity (4.8.7) is valid when $\left|\mathop{\mathrm{ph}\/}\nolimits z\right|\leq\pi$ . For another example see (4.2.37).

In the DLMF it is usually clear from the context which definition of principal value is being used. However, in the absence of any indication to the contrary it is assumed that the definition is the closed one. For other examples in this chapter see §§4.23, 4.24, 4.37, and 4.38.

§4.2(ii) Logarithms to a General Base $a$

Notes:: See Hobson (1928, pp. 296–301).
Defines:: $\mathop{\mathrm{log}_{{a}}\/}\nolimits z$ : logarithm to general base $a$
Keywords:: logarithm function
Referenced by:: §3.12
Permalink:: http://dlmf.nist.gov/4.2.ii

With $a,b\neq 0$ or 1,

4.2.8 $\mathop{\mathrm{log}_{{a}}\/}\nolimits z=\ifrac{\mathop{\ln\/}\nolimits z}{\mathop{\ln\/}\nolimits a},$

Symbols:: $\mathop{\mathrm{log}_{{a}}\/}\nolimits z$ : logarithm to general base $a$ , $\mathop{\ln\/}\nolimits z$ : principal branch of logarithm function, $a$ : real or complex constant and $z$ : complex variable
A&S Ref:: 4.1.18
Permalink:: http://dlmf.nist.gov/4.2.E8
Encodings:: TeX, pMML, png

4.2.9 $\mathop{\mathrm{log}_{{a}}\/}\nolimits z=\frac{\mathop{\mathrm{log}_{{b}}\/}\nolimits z}{\mathop{\mathrm{log}_{{b}}\/}\nolimits a},$

Symbols:: $\mathop{\mathrm{log}_{{a}}\/}\nolimits z$ : logarithm to general base $a$ , $a$ : real or complex constant and $z$ : complex variable
A&S Ref:: 4.1.19
Permalink:: http://dlmf.nist.gov/4.2.E9
Encodings:: TeX, pMML, png

4.2.10 $\mathop{\mathrm{log}_{{a}}\/}\nolimits b=\frac{1}{\mathop{\mathrm{log}_{{b}}\/}\nolimits a}.$

Symbols:: $\mathop{\mathrm{log}_{{a}}\/}\nolimits z$ : logarithm to general base $a$ and $a$ : real or complex constant
A&S Ref:: 4.1.20
Permalink:: http://dlmf.nist.gov/4.2.E10
Encodings:: TeX, pMML, png

Natural logarithms have as base the unique positive number

4.2.11 $e=2.71828\ 18284\ 59045\ 23536\dots$

Notes:: For more digits see OEIS Sequence A001113; see also Sloane (2003).
Defines:: $e$ : base of exponential function
A&S Ref:: 4.2.22 (with 10D value)
Permalink:: http://dlmf.nist.gov/4.2.E11
Encodings:: TeX, pMML, png

such that

4.2.12 $\mathop{\ln\/}\nolimits e=1.$

Symbols:: $e$ : base of exponential function and $\mathop{\ln\/}\nolimits z$ : principal branch of logarithm function
Permalink:: http://dlmf.nist.gov/4.2.E12
Encodings:: TeX, pMML, png

Equivalently,

4.2.13 $\int _{1}^{e}\frac{dt}{t}=1.$

Symbols:: $dx$ : differential of $x$ , $e$ : base of exponential function and $\int$ : integral
Permalink:: http://dlmf.nist.gov/4.2.E13
Encodings:: TeX, pMML, png

Thus

4.2.14 $\mathop{\mathrm{log}_{{e}}\/}\nolimits z=\mathop{\ln\/}\nolimits z,$

Symbols:: $e$ : base of exponential function, $\mathop{\mathrm{log}_{{a}}\/}\nolimits z$ : logarithm to general base $a$ , $\mathop{\ln\/}\nolimits z$ : principal branch of logarithm function and $z$ : complex variable
A&S Ref:: 4.1.21
Permalink:: http://dlmf.nist.gov/4.2.E14
Encodings:: TeX, pMML, png

4.2.15 $\mathop{\mathrm{log}_{{10}}\/}\nolimits z=\ifrac{(\mathop{\ln\/}\nolimits z)}{(\mathop{\ln\/}\nolimits 10)}=(\mathop{\mathrm{log}_{{10}}\/}\nolimits e)\mathop{\ln\/}\nolimits z,$

Symbols:: $e$ : base of exponential function, $\mathop{\mathrm{log}_{{a}}\/}\nolimits z$ : logarithm to general base $a$ , $\mathop{\ln\/}\nolimits z$ : principal branch of logarithm function and $z$ : complex variable
A&S Ref:: 4.1.22
Permalink:: http://dlmf.nist.gov/4.2.E15
Encodings:: TeX, pMML, png

4.2.16 $\mathop{\ln\/}\nolimits z=(\mathop{\ln\/}\nolimits 10)\mathop{\mathrm{log}_{{10}}\/}\nolimits z,$

Symbols:: $\mathop{\mathrm{log}_{{a}}\/}\nolimits z$ : logarithm to general base $a$ , $\mathop{\ln\/}\nolimits z$ : principal branch of logarithm function and $z$ : complex variable
A&S Ref:: 4.1.23
Permalink:: http://dlmf.nist.gov/4.2.E16
Encodings:: TeX, pMML, png

4.2.17 $\mathop{\mathrm{log}_{{10}}\/}\nolimits e=0.43429\ 44819\ 0 3251\ 82765\dots,$

Notes:: For more digits see OEIS Sequence A002285; see also Sloane (2003).
Symbols:: $e$ : base of exponential function and $\mathop{\mathrm{log}_{{a}}\/}\nolimits z$ : logarithm to general base $a$
A&S Ref:: 4.1.22 (with 10D value)
Permalink:: http://dlmf.nist.gov/4.2.E17
Encodings:: TeX, pMML, png

4.2.18 $\mathop{\ln\/}\nolimits 10=2.30258\ 50929\ 94045\ 68401\dots.$

Notes:: For more digits see OEIS Sequence A002392; see also Sloane (2003).
Symbols:: $\mathop{\ln\/}\nolimits z$ : principal branch of logarithm function
A&S Ref:: 4.1.23 (with 10D value.)
Permalink:: http://dlmf.nist.gov/4.2.E18
Encodings:: TeX, pMML, png

$\mathop{\mathrm{log}_{{e}}\/}\nolimits x=\mathop{\ln\/}\nolimits x$ is also called the Napierian or hyperbolic logarithm. $\mathop{\mathrm{log}_{{10}}\/}\nolimits x$ is the common or Briggs logarithm.

§4.2(iii) The Exponential Function

Notes:: See Hobson (1928, pp. 289–296).
Keywords:: exponential function, power series
Permalink:: http://dlmf.nist.gov/4.2.iii

4.2.19 $\mathop{\exp\/}\nolimits z=1+\frac{z}{1!}+\frac{z^{2}}{2!}+\frac{z^{3}}{3!}+\cdots.$

Defines:: $\mathop{\exp\/}\nolimits z$ : exponential function
Symbols:: $!$ : $n!$ : factorial and $z$ : complex variable
A&S Ref:: 4.2.1
Referenced by:: ¶ ‣ §4.45(i)
Permalink:: http://dlmf.nist.gov/4.2.E19
Encodings:: TeX, pMML, png

The function $\mathop{\exp\/}\nolimits$ is an entire function of $z$ , with no real or complex zeros. It has period $2\pi i$ :

4.2.20 $\mathop{\exp\/}\nolimits\!\left(z+2\pi i\right)=\mathop{\exp\/}\nolimits z.$

Symbols:: $\mathop{\exp\/}\nolimits z$ : exponential function and $z$ : complex variable
Permalink:: http://dlmf.nist.gov/4.2.E20
Encodings:: TeX, pMML, png

Also,

4.2.21 $\mathop{\exp\/}\nolimits\!\left(-z\right)=1/\mathop{\exp\/}\nolimits\!\left(z\right).$

Symbols:: $\mathop{\exp\/}\nolimits z$ : exponential function and $z$ : complex variable
Permalink:: http://dlmf.nist.gov/4.2.E21
Encodings:: TeX, pMML, png

4.2.22 $|\mathop{\exp\/}\nolimits z|=\mathop{\exp\/}\nolimits\!\left(\realpart{z}\right).$

Symbols:: $\mathop{\exp\/}\nolimits z$ : exponential function, $\realpart{}$ : real part and $z$ : complex variable
A&S Ref:: 4.2.13
Permalink:: http://dlmf.nist.gov/4.2.E22
Encodings:: TeX, pMML, png

The general value of the phase is given by

4.2.23 $\mathop{\mathrm{ph}\/}\nolimits\!\left(\mathop{\exp\/}\nolimits z\right)=\imagpart{z}+2k\pi,$ $k\in\Integer$ .

Symbols:: $\in$ : element of, $\mathop{\exp\/}\nolimits z$ : exponential function, $\imagpart{}$ : imaginary part, $\Integer$ : set of all integers, $\mathop{\mathrm{ph}\/}\nolimits$ : phase, $k$ : integer and $z$ : complex variable
A&S Ref:: 4.2.14 (modified)
Permalink:: http://dlmf.nist.gov/4.2.E23
Encodings:: TeX, pMML, png

If $z=x+iy$ , then

4.2.24 $\mathop{\exp\/}\nolimits z=e^{x}\mathop{\cos\/}\nolimits y+ie^{x}\mathop{\sin\/}\nolimits y.$

Symbols:: $\mathop{\cos\/}\nolimits z$ : cosine function, $\mathop{\exp\/}\nolimits z$ : exponential function, $e$ : base of exponential function, $\mathop{\sin\/}\nolimits z$ : sine function, $x$ : real variable, $y$ : real variable and $z$ : complex variable
Permalink:: http://dlmf.nist.gov/4.2.E24
Encodings:: TeX, pMML, png

If $\zeta\neq 0$ then

4.2.25 $\mathop{\exp\/}\nolimits z=\zeta\;\;\Longleftrightarrow\;\; z=\mathop{\mathrm{Ln}\/}\nolimits\zeta.$

Symbols:: $\mathop{\exp\/}\nolimits z$ : exponential function, $\mathop{\mathrm{Ln}\/}\nolimits z$ : general logarithm function and $z$ : complex variable
A&S Ref:: 4.2.4
Permalink:: http://dlmf.nist.gov/4.2.E25
Encodings:: TeX, pMML, png

§4.2(iv) Powers

Notes:: See Levinson and Redheffer (1970, pp. 62–67).
Keywords:: power function
Referenced by:: ¶ ‣ §1.10(i), ¶ ‣ §1.10(vi), ¶ ‣ §1.9(vi), ¶ ‣ §10.2(ii), ¶ ‣ §16.11(ii), §16.11(ii), §33.7
Permalink:: http://dlmf.nist.gov/4.2.iv

¶ Powers with General Bases

Keywords:: power function

The general $a^{{\rm th}}$ power of $z$ is defined by

4.2.26 $z^{a}=\mathop{\exp\/}\nolimits\!\left(a\mathop{\mathrm{Ln}\/}\nolimits z\right),$ $z\neq 0$ .

Symbols:: $\mathop{\exp\/}\nolimits z$ : exponential function, $\mathop{\mathrm{Ln}\/}\nolimits z$ : general logarithm function, $a$ : real or complex constant and $z$ : complex variable
Permalink:: http://dlmf.nist.gov/4.2.E26
Encodings:: TeX, pMML, png

In particular, $z^{0}=1$ , and if $a=n=1,2,3,\dots$ , then

4.2.27 $z^{a}=\underbrace{z\cdot z\cdots z}_{{n\text{ times}}}=1/z^{{-a}}.$

Symbols:: $n$ : integer, $z$ : complex variable and $a=n$ : integer
Permalink:: http://dlmf.nist.gov/4.2.E27
Encodings:: TeX, pMML, png

In all other cases, $z^{a}$ is a multivalued function with branch point at $z=0$ . The principal value is

4.2.28 $z^{a}=\mathop{\exp\/}\nolimits\!\left(a\mathop{\ln\/}\nolimits z\right).$

Symbols:: $\mathop{\exp\/}\nolimits z$ : exponential function, $\mathop{\ln\/}\nolimits z$ : principal branch of logarithm function, $a$ : real or complex constant and $z$ : complex variable
A&S Ref:: 4.2.7
Permalink:: http://dlmf.nist.gov/4.2.E28
Encodings:: TeX, pMML, png

This is an analytic function of $z$ on $\Complex\setminus(-\infty,0]$ , and is two-valued and discontinuous on the cut shown in Figure 4.2.1, unless $a\in\Integer$ .

4.2.29 $|z^{a}|=|z|^{{\realpart{a}}}\mathop{\exp\/}\nolimits\!\left(-(\imagpart{a})\mathop{\mathrm{ph}\/}\nolimits z\right),$

Symbols:: $\mathop{\exp\/}\nolimits z$ : exponential function, $\imagpart{}$ : imaginary part, $\mathop{\mathrm{ph}\/}\nolimits$ : phase, $\realpart{}$ : real part, $a$ : real or complex constant and $z$ : complex variable
A&S Ref:: 4.2.9
Permalink:: http://dlmf.nist.gov/4.2.E29
Encodings:: TeX, pMML, png

4.2.30 $\mathop{\mathrm{ph}\/}\nolimits\!\left(z^{a}\right)=(\realpart{a})\mathop{\mathrm{ph}\/}\nolimits z+(\imagpart{a})\mathop{\ln\/}\nolimits|z|,$

Symbols:: $\imagpart{}$ : imaginary part, $\mathop{\ln\/}\nolimits z$ : principal branch of logarithm function, $\mathop{\mathrm{ph}\/}\nolimits$ : phase, $\realpart{}$ : real part, $a$ : real or complex constant and $z$ : complex variable
A&S Ref:: 4.2.10
Permalink:: http://dlmf.nist.gov/4.2.E30
Encodings:: TeX, pMML, png

where $\mathop{\mathrm{ph}\/}\nolimits z\in[-\pi,\pi]$ for the principal value of $z^{a}$ , and is unrestricted in the general case. When $a$ is real

4.2.31

$|z^{a}|=|z|^{a},$

$\mathop{\mathrm{ph}\/}\nolimits\!\left(z^{a}\right)=a\mathop{\mathrm{ph}\/}\nolimits z.$

Symbols:: $\mathop{\mathrm{ph}\/}\nolimits$ : phase, $a$ : real or complex constant and $z$ : complex variable
Permalink:: http://dlmf.nist.gov/4.2.E31
Encodings:: TeX, TeX, pMML, pMML, png, png

Unless indicated otherwise, it is assumed throughout the DLMF that a power assumes its principal value. With this convention,

4.2.32 $e^{z}=\mathop{\exp\/}\nolimits z,$

Symbols:: $\mathop{\exp\/}\nolimits z$ : exponential function, $e$ : base of exponential function and $z$ : complex variable
Permalink:: http://dlmf.nist.gov/4.2.E32
Encodings:: TeX, pMML, png

but the general value of $e^{z}$ is

4.2.33 $e^{z}=(\mathop{\exp\/}\nolimits z)\mathop{\exp\/}\nolimits\!\left(2kz\pi i\right),$ $k\in\Integer$ .

Symbols:: $\in$ : element of, $\mathop{\exp\/}\nolimits z$ : exponential function, $e$ : base of exponential function, $\Integer$ : set of all integers, $k$ : integer and $z$ : complex variable
Permalink:: http://dlmf.nist.gov/4.2.E33
Encodings:: TeX, pMML, png

For $z=1$

4.2.34 $e=1+\frac{1}{1!}+\frac{1}{2!}+\frac{1}{3!}+\cdots.$

Symbols:: $e$ : base of exponential function and $!$ : $n!$ : factorial
Permalink:: http://dlmf.nist.gov/4.2.E34
Encodings:: TeX, pMML, png

If $z^{a}$ has its general value, with $a\neq 0$ , and if $w\neq 0$ , then

4.2.35 $z^{a}=w\;\;\Longleftrightarrow\;\; z=\mathop{\exp\/}\nolimits\!\left(\frac{1}{a}\mathop{\mathrm{Ln}\/}\nolimits w\right).$

Symbols:: $\mathop{\exp\/}\nolimits z$ : exponential function, $\mathop{\mathrm{Ln}\/}\nolimits z$ : general logarithm function, $z$ : complex variable and $a\neq 0$ : complex constant
Permalink:: http://dlmf.nist.gov/4.2.E35
Encodings:: TeX, pMML, png

This result is also valid when $z^{a}$ has its principal value, provided that the branch of $\mathop{\mathrm{Ln}\/}\nolimits w$ satisfies

4.2.36 $-\pi\leq\imagpart{\left(\frac{1}{a}\mathop{\mathrm{Ln}\/}\nolimits w\right)}\leq\pi.$

Symbols:: $\imagpart{}$ : imaginary part, $\mathop{\mathrm{Ln}\/}\nolimits z$ : general logarithm function and $a$ : real or complex constant
Permalink:: http://dlmf.nist.gov/4.2.E36
Encodings:: TeX, pMML, png

Another example of a principal value is provided by

4.2.37 $\sqrt{z^{2}}=\begin{cases}z,&\realpart{z}\geq 0,\\ -z,&\realpart{z}\leq 0.\end{cases}$

Symbols:: $\realpart{}$ : real part and $z$ : complex variable
Referenced by:: §4.2(i)
Permalink:: http://dlmf.nist.gov/4.2.E37
Encodings:: TeX, pMML, png

Again, without the closed definition the $\geq$ and $\leq$ signs would have to be replaced by $>$ and $<$ , respectively.