§4.3 Graphics
Contents
- §4.3(i) Real Arguments
- §4.3(ii) Complex Arguments: Conformal Maps
- §4.3(iii) Complex Arguments: Surfaces
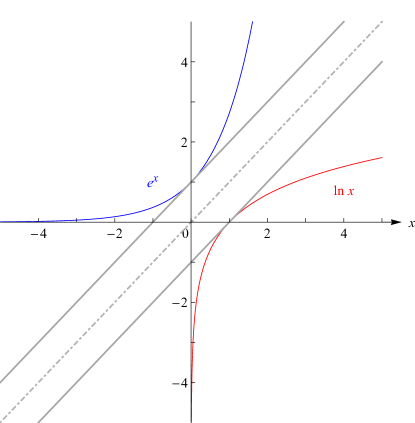
§4.3(i) Real Arguments
§4.3(ii) Complex Arguments: Conformal Maps
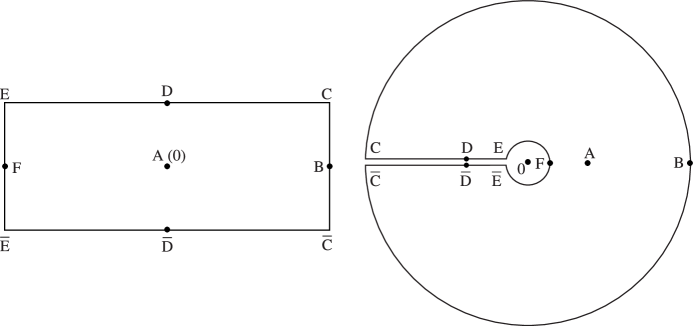
Figure 4.3.2 illustrates the conformal mapping of the strip onto the whole -plane cut along the negative real axis, where and (principal value). Corresponding points share the same letters, with bars signifying complex conjugates. Lines parallel to the real axis in the -plane map onto rays in the -plane, and lines parallel to the imaginary axis in the -plane map onto circles centered at the origin in the -plane. In the labeling of corresponding points is a real parameter that can lie anywhere in the interval .
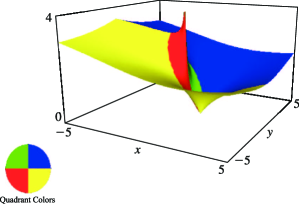
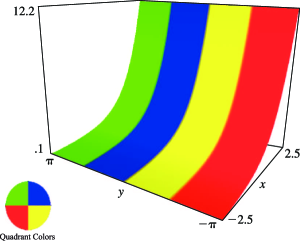
§4.3(iii) Complex Arguments: Surfaces
In the graphics shown in this subsection height corresponds to the absolute value of the function and color to the phase. See also About Color Map.