§25.12 Polylogarithms

Permalink:: http://dlmf.nist.gov/25.12

§25.12(i) Dilogarithms
§25.12(ii) Polylogarithms
§25.12(iii) Fermi–Dirac and Bose–Einstein Integrals

§25.12(i) Dilogarithms

Notes:: See Maximon (2003). The graphics were constructed at NIST.
Keywords:: Clausen’s integral, dilogarithms
Referenced by:: §25.19, §25.20, §25.21(vi)
Permalink:: http://dlmf.nist.gov/25.12.i

The notation $\mathop{\mathrm{Li}_{2}\/}\nolimits\!\left(z\right)$ was introduced in Lewin (1981) for a function discussed in Euler (1768) and called the dilogarithm in Hill (1828):

25.12.1 $\mathop{\mathrm{Li}_{2}\/}\nolimits\!\left(z\right)=\sum_{{n=1}}^{\infty}\frac% {z^{n}}{n^{2}},$ $|z|\leq 1$ .

Defines:: $\mathop{\mathrm{Li}_{2}\/}\nolimits\!\left(z\right)$ : dilogarithm
Symbols:: : nonnegative integer, : real variable and : complex variable
A&S Ref:: 27.7.2 (with )
Referenced by:: §25.12(i), §25.12(i)
Permalink:: http://dlmf.nist.gov/25.12.E1
Encodings:: TeX, pMML, png

25.12.2 $\mathop{\mathrm{Li}_{2}\/}\nolimits\!\left(z\right)=-\int_{0}^{z}t^{{-1}}% \mathop{\ln\/}\nolimits\!\left(1-t\right)dt,$ $z\in\Complex\setminus(1,\infty)$ .

Symbols:: $\Complex$ : complex plane (excluding infinity), : differential of , $\mathop{\mathrm{Li}_{2}\/}\nolimits\!\left(z\right)$ : dilogarithm, $\in$ : element of, $\int$ : integral, $\mathop{\ln\/}\nolimits z$ : principal branch of logarithm function, : open interval, $\setminus$ : set subtraction, : real variable and : complex variable
A&S Ref:: 27.7.1 (is a modified form with )
Referenced by:: §25.12(i)
Permalink:: http://dlmf.nist.gov/25.12.E2
Encodings:: TeX, pMML, png

Other notations and names for $\mathop{\mathrm{Li}_{2}\/}\nolimits\!\left(z\right)$ include $S_{2}(z)$ (Kölbig et al. (1970)), Spence function $\mathrm{Sp}(z)$ (’t Hooft and Veltman (1979)), and $\mathrm{L}_{2}(z)$ (Maximon (2003)).

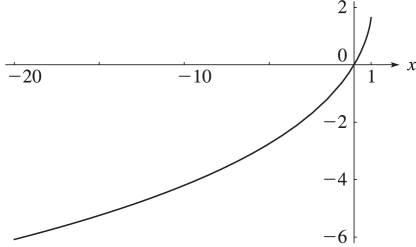
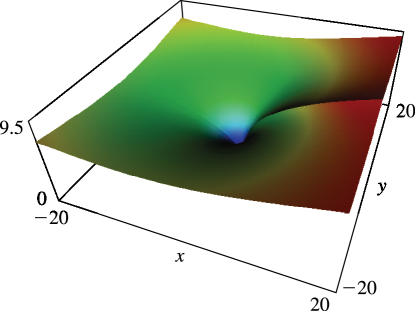
In the complex plane $\mathop{\mathrm{Li}_{2}\/}\nolimits\!\left(z\right)$ has a branch point at . The principal branch has a cut along the interval $[1,\infty)$ and agrees with (25.12.1) when $|z|\leq 1$ ; see also §4.2(i). The remainder of the equations in this subsection apply to principal branches.

25.12.3 $\mathop{\mathrm{Li}_{2}\/}\nolimits\!\left(z\right)+\mathop{\mathrm{Li}_{2}\/}% \nolimits\!\left(\frac{z}{z-1}\right)=-\frac{1}{2}(\mathop{\ln\/}\nolimits\!% \left(1-z\right))^{2},$ $z\in\Complex\setminus[1,\infty)$ .

Symbols:: : half-closed interval, $\Complex$ : complex plane (excluding infinity), $\mathop{\mathrm{Li}_{2}\/}\nolimits\!\left(z\right)$ : dilogarithm, $\in$ : element of, $\mathop{\ln\/}\nolimits z$ : principal branch of logarithm function, $\setminus$ : set subtraction, : real variable and : complex variable
A&S Ref:: 27.7.5 (is a modified form with )
Permalink:: http://dlmf.nist.gov/25.12.E3
Encodings:: TeX, pMML, png

25.12.4 $\mathop{\mathrm{Li}_{2}\/}\nolimits\!\left(z\right)+\mathop{\mathrm{Li}_{2}\/}% \nolimits\!\left(\frac{1}{z}\right)=-\frac{1}{6}\pi^{2}-\frac{1}{2}(\mathop{% \ln\/}\nolimits\!\left(-z\right))^{2},$ $z\in\Complex\setminus[0,\infty)$ .

Symbols:: : half-closed interval, $\Complex$ : complex plane (excluding infinity), $\mathop{\mathrm{Li}_{2}\/}\nolimits\!\left(z\right)$ : dilogarithm, $\in$ : element of, $\mathop{\ln\/}\nolimits z$ : principal branch of logarithm function, $\setminus$ : set subtraction and : complex variable
Referenced by:: ¶ ‣ §25.12(ii)
Permalink:: http://dlmf.nist.gov/25.12.E4
Encodings:: TeX, pMML, png

25.12.5 $\mathop{\mathrm{Li}_{2}\/}\nolimits\!\left(z^{m}\right)=m\sum_{{k=0}}^{{m-1}}% \mathop{\mathrm{Li}_{2}\/}\nolimits\!\left(ze^{{2\pi ik/m}}\right),$ $m=1,2,3,\dots$ ,

Symbols:: $\mathop{\mathrm{Li}_{2}\/}\nolimits\!\left(z\right)$ : dilogarithm, : base of exponential function, : nonnegative integer, : nonnegative integer and : complex variable
Permalink:: http://dlmf.nist.gov/25.12.E5
Encodings:: TeX, pMML, png

25.12.6 $\mathop{\mathrm{Li}_{2}\/}\nolimits\!\left(x\right)+\mathop{\mathrm{Li}_{2}\/}% \nolimits\!\left(1-x\right)=\frac{1}{6}\pi^{2}-(\mathop{\ln\/}\nolimits x)% \mathop{\ln\/}\nolimits\!\left(1-x\right),$

Symbols:: $\mathop{\mathrm{Li}_{2}\/}\nolimits\!\left(z\right)$ : dilogarithm, $\mathop{\ln\/}\nolimits z$ : principal branch of logarithm function and : real variable
Permalink:: http://dlmf.nist.gov/25.12.E6
Encodings:: TeX, pMML, png

When $z=e^{{i\theta}}$ , $0\leq\theta\leq 2\pi$ , (25.12.1) becomes

25.12.7 $\mathop{\mathrm{Li}_{2}\/}\nolimits\!\left(e^{{i\theta}}\right)=\sum_{{n=1}}^{% \infty}\frac{\mathop{\cos\/}\nolimits\!\left(n\theta\right)}{n^{2}}+i\sum_{{n=% 1}}^{\infty}\frac{\mathop{\sin\/}\nolimits\!\left(n\theta\right)}{n^{2}}.$

Symbols:: $\mathop{\cos\/}\nolimits z$ : cosine function, $\mathop{\mathrm{Li}_{2}\/}\nolimits\!\left(z\right)$ : dilogarithm, : base of exponential function, $\mathop{\sin\/}\nolimits z$ : sine function, : nonnegative integer and $\theta$ : phase
Referenced by:: §25.12(i)
Permalink:: http://dlmf.nist.gov/25.12.E7
Encodings:: TeX, pMML, png

The cosine series in (25.12.7) has the elementary sum

25.12.8 $\sum_{{n=1}}^{\infty}\frac{\mathop{\cos\/}\nolimits\!\left(n\theta\right)}{n^{% 2}}=\frac{\pi^{2}}{6}-\frac{\pi\theta}{2}+\frac{\theta^{2}}{4}.$

Symbols:: $\mathop{\cos\/}\nolimits z$ : cosine function, : nonnegative integer and $\theta$ : phase
A&S Ref:: 27.8.6 (second series)
Permalink:: http://dlmf.nist.gov/25.12.E8
Encodings:: TeX, pMML, png

By (25.12.2)

25.12.9 $\sum_{{n=1}}^{\infty}\frac{\mathop{\sin\/}\nolimits\!\left(n\theta\right)}{n^{% 2}}=-\int_{0}^{\theta}\mathop{\ln\/}\nolimits\!\left(2\mathop{\sin\/}\nolimits% \!\left(\tfrac{1}{2}x\right)\right)dx.$

Symbols:: : differential of , $\int$ : integral, $\mathop{\ln\/}\nolimits z$ : principal branch of logarithm function, $\mathop{\sin\/}\nolimits z$ : sine function, : nonnegative integer, : real variable and $\theta$ : phase
A&S Ref:: 27.8.6 (integration of first series)
Referenced by:: §25.19
Permalink:: http://dlmf.nist.gov/25.12.E9
Encodings:: TeX, pMML, png

The right-hand side is called Clausen’s integral.

For graphics see Figures 25.12.1 and 25.12.2, and for further properties see Maximon (2003), Kirillov (1995), Lewin (1981), Nielsen (1909), and Zagier (1989).

Figure 25.12.1: Dilogarithm function $\mathop{\mathrm{Li}_{2}\/}\nolimits\!\left(x\right)$ , $-20\leq x<1.$

Symbols:: $\mathop{\mathrm{Li}_{2}\/}\nolimits\!\left(z\right)$ : dilogarithm and : real variable
Referenced by:: §25.12(i)
Permalink:: http://dlmf.nist.gov/25.12.F1
Encodings:: pdf, png

Visualization Help

Figure 25.12.2: Absolute value of the dilogarithm function $\left|\mathop{\mathrm{Li}_{2}\/}\nolimits\!\left(x+iy\right)\right|$ , $-20\leq x\leq 20$ , $-20\leq y\leq 20$ . Principal value. There is a cut along the real axis from 1 to $\infty$ .

Symbols:: $\mathop{\mathrm{Li}_{2}\/}\nolimits\!\left(z\right)$ : dilogarithm and : real variable
Referenced by:: §25.12(i)
Permalink:: http://dlmf.nist.gov/25.12.F2
Encodings:: VRML, X3D, pdf, png

§25.12(ii) Polylogarithms

Notes:: See Erdélyi et al. (1953a, pp. 27 and 29). For (25.12.13) see Erdélyi et al. (1953a, p. 31) with change of notation.
Defines:: $\mathop{\phi\/}\nolimits\!\left(z,s\right)=\mathop{\mathrm{Li}_{{s}}\/}% \nolimits\!\left(z\right)$ : notation used by (Truesdell, 1945)
Keywords:: Riemann zeta function, polylogarithms
Referenced by:: §25.14(i)
Permalink:: http://dlmf.nist.gov/25.12.ii

For real or complex and the polylogarithm $\mathop{\mathrm{Li}_{{s}}\/}\nolimits\!\left(z\right)$ is defined by

25.12.10 $\mathop{\mathrm{Li}_{{s}}\/}\nolimits\!\left(z\right)=\sum_{{n=1}}^{\infty}% \frac{z^{n}}{n^{s}}.$

Defines:: $\mathop{\mathrm{Li}_{{s}}\/}\nolimits\!\left(z\right)$ : polylogarithm
Symbols:: : nonnegative integer, : complex variable and : complex variable
Permalink:: http://dlmf.nist.gov/25.12.E10
Encodings:: TeX, pMML, png

For each fixed complex the series defines an analytic function of for . The series also converges when , provided that $\realpart{s}>1$ . For other values of , $\mathop{\mathrm{Li}_{{s}}\/}\nolimits\!\left(z\right)$ is defined by analytic continuation.

The notation $\mathop{\phi\/}\nolimits\!\left(z,s\right)$ was used for $\mathop{\mathrm{Li}_{{s}}\/}\nolimits\!\left(z\right)$ in Truesdell (1945) for a series treated in Jonquière (1889), hence the alternative name Jonquière’s function. The special case is the Riemann zeta function: $\mathop{\zeta\/}\nolimits\!\left(s\right)=\mathop{\mathrm{Li}_{{s}}\/}% \nolimits\!\left(1\right)$ .

¶ Integral Representation

Keywords:: Hurwitz zeta function, Riemann zeta function, polylogarithms

25.12.11 $\mathop{\mathrm{Li}_{{s}}\/}\nolimits\!\left(z\right)=\frac{z}{\mathop{\Gamma% \/}\nolimits\!\left(s\right)}\int_{0}^{\infty}\frac{x^{{s-1}}}{e^{x}-z}dx,$

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, : differential of , : base of exponential function, $\int$ : integral, $\mathop{\mathrm{Li}_{{s}}\/}\nolimits\!\left(z\right)$ : polylogarithm, : real variable, : complex variable and : complex variable
Referenced by:: ¶ ‣ §25.12(ii)
Permalink:: http://dlmf.nist.gov/25.12.E11
Encodings:: TeX, pMML, png

valid when $\realpart{s}>0$ and $\left|\mathop{\mathrm{ph}\/}\nolimits\!\left(1-z\right)\right|<\pi$ , or $\realpart{s}>1$ and . (In the latter case (25.12.11) becomes (25.5.1)).

Further properties include

25.12.12 $\mathop{\mathrm{Li}_{{s}}\/}\nolimits\!\left(z\right)=\mathop{\Gamma\/}% \nolimits\!\left(1-s\right)\left(\mathop{\ln\/}\nolimits\frac{1}{z}\right)^{{s% -1}}+\sum_{{n=0}}^{\infty}\mathop{\zeta\/}\nolimits\!\left(s-n\right)\frac{(% \mathop{\ln\/}\nolimits z)^{n}}{n!},$ $s\neq 1,2,3,\dots$ , $|\mathop{\ln\/}\nolimits z|<2\pi$ ,

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, $\mathop{\zeta\/}\nolimits\!\left(s\right)$ : Riemann zeta function, : : factorial, $\mathop{\ln\/}\nolimits z$ : principal branch of logarithm function, $\mathop{\mathrm{Li}_{{s}}\/}\nolimits\!\left(z\right)$ : polylogarithm, : nonnegative integer, : complex variable and : complex variable
Permalink:: http://dlmf.nist.gov/25.12.E12
Encodings:: TeX, pMML, png

and

25.12.13 $\mathop{\mathrm{Li}_{{s}}\/}\nolimits\!\left(e^{{2\pi ia}}\right)+e^{{\pi is}}% \mathop{\mathrm{Li}_{{s}}\/}\nolimits\!\left(e^{{-2\pi ia}}\right)=\frac{(2\pi% )^{s}e^{{\pi is/2}}}{\mathop{\Gamma\/}\nolimits\!\left(s\right)}\mathop{\zeta% \/}\nolimits\!\left(1-s,a\right),$

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, $\mathop{\zeta\/}\nolimits\!\left(s,a\right)$ : Hurwitz zeta function, : base of exponential function, $\mathop{\mathrm{Li}_{{s}}\/}\nolimits\!\left(z\right)$ : polylogarithm, : real or complex parameter and : complex variable
Referenced by:: ¶ ‣ §25.12(ii), §25.12(ii)
Permalink:: http://dlmf.nist.gov/25.12.E13
Encodings:: TeX, pMML, png

valid when $\realpart{s}>0$ , $\imagpart{a}>0$ or $\realpart{s}>1$ , $\imagpart{a}=0$ . When and $e^{{2\pi ia}}=z$ , (25.12.13) becomes (25.12.4).

See also Lewin (1981), Kölbig (1986), Maximon (2003), Prudnikov et al. (1990, §§1.2 and 2.5), Prudnikov et al. (1992a, §3.3), and Prudnikov et al. (1992b, §3.3).