Julia sets

SearchAdvancedHelp

(0.001 seconds)

11—20 of 566 matching pages

11: 22.5 Special Values

… ►For example, at $z=K+\mathrm{i}{K}^{\prime }$, $\mathrm{sn}(z,k)=1/k$, $d\mathrm{sn}(z,k)/dz=0$. … ►For example, $\mathrm{sn}(\frac{1}{2}K,k)={(1+k^{\prime })}^{-1/2}$. … ►

Table 22.5.2: Other special values of Jacobian elliptic functions.

► ►►►

	$z$
…
$\mathrm{sn}z$	${(1+k^{\prime })}^{-1/2}$	$\left({(1+k)}^{1/2}+\mathrm{i}{(1-k)}^{1/2}\right)/{(2k)}^{1/2}$	$\mathrm{i}{k}^{-1/2}$
…

►

… ►If $k\to 0+$, then $K\to \pi /2$ and $K^{\prime }\to \mathrm{\infty }$; if $k\to 1-$, then $K\to \mathrm{\infty }$ and $K^{\prime }\to \pi /2$. … ►For values of $K,K^{\prime }$ when $k^2=\frac{1}{2}$ (lemniscatic case) see §23.5(iii), and for $k^2={\mathrm{e}}^{\mathrm{i}\pi /3}$ (equianharmonic case) see §23.5(v). …

12: 10.55 Continued Fractions

… ►For continued fractions for ${𝗃}_{n+1}\left(z\right)/{𝗃}_n\left(z\right)$ and ${𝗂}_{n+1}^{(1)}\left(z\right)/{𝗂}_n^{(1)}\left(z\right)$ see Cuyt et al. (2008, pp. 350, 353, 362, 363, 367–369).

13: 12.6 Continued Fraction

… ►For a continued-fraction expansion of the ratio $U(a,x)/U(a-1,x)$ see Cuyt et al. (2008, pp. 340–341).

14: 9.6 Relations to Other Functions

… ►

9.6.3 $${\mathrm{Ai}}^{\prime }\left(z\right)=-{\pi }^{-1}(z/\sqrt{3})K_{\pm 2/3}\left(\zeta \right)=(z/3)\left(I_{2/3}\left(\zeta \right)-I_{-2/3}\left(\zeta \right)\right)=\frac{1}{2}(z/\sqrt{3}){\mathrm{e}}^{-\pi \mathrm{i}/6}{H}_{2/3}^{(1)}\left(\zeta {\mathrm{e}}^{\pi \mathrm{i}/2}\right)=\frac{1}{2}(z/\sqrt{3}){\mathrm{e}}^{-5\pi \mathrm{i}/6}{H}_{-2/3}^{(1)}\left(\zeta {\mathrm{e}}^{\pi \mathrm{i}/2}\right)=\frac{1}{2}(z/\sqrt{3}){\mathrm{e}}^{\pi \mathrm{i}/6}{H}_{2/3}^{(2)}\left(\zeta {\mathrm{e}}^{-\pi \mathrm{i}/2}\right)=\frac{1}{2}(z/\sqrt{3}){\mathrm{e}}^{5\pi \mathrm{i}/6}{H}_{-2/3}^{(2)}\left(\zeta {\mathrm{e}}^{-\pi \mathrm{i}/2}\right),$$

ⓘ

Symbols:

$\mathrm{Ai}\left(z\right)$: Airy function, $H_{\nu }^{(1)}\left(z\right)$: Bessel function of the third kind (or Hankel function), $H_{\nu }^{(2)}\left(z\right)$: Bessel function of the third kind (or Hankel function), $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{e}$: base of natural logarithm, $\mathrm{i}$: imaginary unit, $I_{\nu }\left(z\right)$: modified Bessel function of the first kind, $K_{\nu }\left(z\right)$: modified Bessel function of the second kind, $z$: complex variable and $\zeta$: change of variable

Proof sketch:

Derivable from those given in Miller (1946, p. B17) and Olver (1997b, pp. 392–393).

A&S Ref:

10.4.16 (with opposite sign!)

Referenced by:

(9.6.22)

Permalink:

http://dlmf.nist.gov/9.6.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §9.6(i), §9.6 and Ch.9

… ►

9.6.6 $$\mathrm{Ai}\left(-z\right)=(\sqrt{z}/3)\left(J_{1/3}\left(\zeta \right)+J_{-1/3}\left(\zeta \right)\right)=\frac{1}{2}\sqrt{z/3}\left({\mathrm{e}}^{\pi \mathrm{i}/6}{H}_{1/3}^{(1)}\left(\zeta \right)+{\mathrm{e}}^{-\pi \mathrm{i}/6}{H}_{1/3}^{(2)}\left(\zeta \right)\right)=\frac{1}{2}\sqrt{z/3}\left({\mathrm{e}}^{-\pi \mathrm{i}/6}{H}_{-1/3}^{(1)}\left(\zeta \right)+{\mathrm{e}}^{\pi \mathrm{i}/6}{H}_{-1/3}^{(2)}\left(\zeta \right)\right),$$

ⓘ

Symbols:

$\mathrm{Ai}\left(z\right)$: Airy function, $J_{\nu }\left(z\right)$: Bessel function of the first kind, $H_{\nu }^{(1)}\left(z\right)$: Bessel function of the third kind (or Hankel function), $H_{\nu }^{(2)}\left(z\right)$: Bessel function of the third kind (or Hankel function), $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{e}$: base of natural logarithm, $\mathrm{i}$: imaginary unit, $z$: complex variable and $\zeta$: change of variable

Proof sketch:

Derivable from those given in Miller (1946, p. B17) and Olver (1997b, pp. 392–393).

A&S Ref:

10.4.15 (partial)

Permalink:

http://dlmf.nist.gov/9.6.E6

Encodings:

pMML, png, TeX

See also:

Annotations for §9.6(i), §9.6 and Ch.9

►

9.6.7 $${\mathrm{Ai}}^{\prime }\left(-z\right)=(z/3)\left(J_{2/3}\left(\zeta \right)-J_{-2/3}\left(\zeta \right)\right)=\frac{1}{2}(z/\sqrt{3})\left({\mathrm{e}}^{-\pi \mathrm{i}/6}{H}_{2/3}^{(1)}\left(\zeta \right)+{\mathrm{e}}^{\pi \mathrm{i}/6}{H}_{2/3}^{(2)}\left(\zeta \right)\right)=\frac{1}{2}(z/\sqrt{3})\left({\mathrm{e}}^{-5\pi \mathrm{i}/6}{H}_{-2/3}^{(1)}\left(\zeta \right)+{\mathrm{e}}^{5\pi \mathrm{i}/6}{H}_{-2/3}^{(2)}\left(\zeta \right)\right),$$

ⓘ

Symbols:

$\mathrm{Ai}\left(z\right)$: Airy function, $J_{\nu }\left(z\right)$: Bessel function of the first kind, $H_{\nu }^{(1)}\left(z\right)$: Bessel function of the third kind (or Hankel function), $H_{\nu }^{(2)}\left(z\right)$: Bessel function of the third kind (or Hankel function), $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{e}$: base of natural logarithm, $\mathrm{i}$: imaginary unit, $z$: complex variable and $\zeta$: change of variable

Proof sketch:

Derivable from those given in Miller (1946, p. B17) and Olver (1997b, pp. 392–393).

A&S Ref:

10.4.17 (partial)

Permalink:

http://dlmf.nist.gov/9.6.E7

Encodings:

pMML, png, TeX

See also:

Annotations for §9.6(i), §9.6 and Ch.9

►

9.6.8 $$\mathrm{Bi}\left(-z\right)=\sqrt{z/3}\left(J_{-1/3}\left(\zeta \right)-J_{1/3}\left(\zeta \right)\right)=\frac{1}{2}\sqrt{z/3}\left({\mathrm{e}}^{2\pi \mathrm{i}/3}{H}_{1/3}^{(1)}\left(\zeta \right)+{\mathrm{e}}^{-2\pi \mathrm{i}/3}{H}_{1/3}^{(2)}\left(\zeta \right)\right)=\frac{1}{2}\sqrt{z/3}\left({\mathrm{e}}^{\pi \mathrm{i}/3}{H}_{-1/3}^{(1)}\left(\zeta \right)+{\mathrm{e}}^{-\pi \mathrm{i}/3}{H}_{-1/3}^{(2)}\left(\zeta \right)\right),$$

ⓘ

Symbols:

$\mathrm{Bi}\left(z\right)$: Airy function, $J_{\nu }\left(z\right)$: Bessel function of the first kind, $H_{\nu }^{(1)}\left(z\right)$: Bessel function of the third kind (or Hankel function), $H_{\nu }^{(2)}\left(z\right)$: Bessel function of the third kind (or Hankel function), $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{e}$: base of natural logarithm, $\mathrm{i}$: imaginary unit, $z$: complex variable and $\zeta$: change of variable

Proof sketch:

Derivable from those given in Miller (1946, p. B17) and Olver (1997b, pp. 392–393).

A&S Ref:

10.4.19 (in slightly different form)

Permalink:

http://dlmf.nist.gov/9.6.E8

Encodings:

pMML, png, TeX

See also:

Annotations for §9.6(i), §9.6 and Ch.9

►

9.6.9 $${\mathrm{Bi}}^{\prime }\left(-z\right)=(z/\sqrt{3})\left(J_{-2/3}\left(\zeta \right)+J_{2/3}\left(\zeta \right)\right)=\frac{1}{2}(z/\sqrt{3})\left({\mathrm{e}}^{\pi \mathrm{i}/3}{H}_{2/3}^{(1)}\left(\zeta \right)+{\mathrm{e}}^{-\pi \mathrm{i}/3}{H}_{2/3}^{(2)}\left(\zeta \right)\right)=\frac{1}{2}(z/\sqrt{3})\left({\mathrm{e}}^{-\pi \mathrm{i}/3}{H}_{-2/3}^{(1)}\left(\zeta \right)+{\mathrm{e}}^{\pi \mathrm{i}/3}{H}_{-2/3}^{(2)}\left(\zeta \right)\right).$$

ⓘ

Symbols:

$\mathrm{Bi}\left(z\right)$: Airy function, $J_{\nu }\left(z\right)$: Bessel function of the first kind, $H_{\nu }^{(1)}\left(z\right)$: Bessel function of the third kind (or Hankel function), $H_{\nu }^{(2)}\left(z\right)$: Bessel function of the third kind (or Hankel function), $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{e}$: base of natural logarithm, $\mathrm{i}$: imaginary unit, $z$: complex variable and $\zeta$: change of variable

Proof sketch:

Derivable from those given in Miller (1946, p. B17) and Olver (1997b, pp. 392–393).

A&S Ref:

10.4.21 (partial)

Permalink:

http://dlmf.nist.gov/9.6.E9

Encodings:

pMML, png, TeX

See also:

Annotations for §9.6(i), §9.6 and Ch.9

…

15: 10.62 Graphs

… ►

►►

Figure 10.62.3: ${\mathrm{e}}^{-x/\sqrt{2}}\mathrm{ber}x$, ${\mathrm{e}}^{-x/\sqrt{2}}\mathrm{bei}x$, ${\mathrm{e}}^{-x/\sqrt{2}}M\left(x\right)$, $0\le x\le 8$. Magnify

►

►►

Figure 10.62.4: ${\mathrm{e}}^{x/\sqrt{2}}\ker x$, ${\mathrm{e}}^{x/\sqrt{2}}\mathrm{kei}x$, ${\mathrm{e}}^{x/\sqrt{2}}N\left(x\right)$, $0\le x\le 8$. Magnify

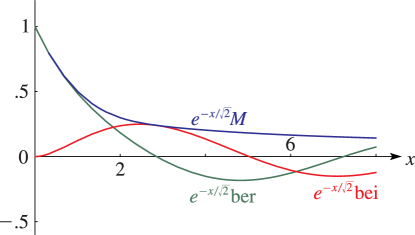
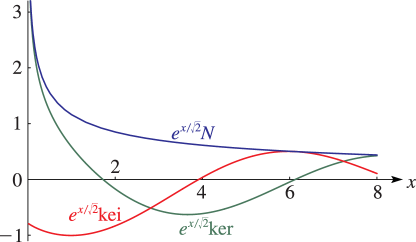
16: 11.8 Analogs to Kelvin Functions

§11.8 Analogs to Kelvin Functions

►For properties of Struve functions of argument $x{\mathrm{e}}^{\pm 3\pi \mathrm{i}/4}$ see McLachlan and Meyers (1936).

17: 4.17 Special Values and Limits

… ►

Table 4.17.1: Trigonometric functions: values at multiples of $\frac{1}{12}\pi$.

► ►►►►►►►

$\theta$	$\sin \theta$	$\cos \theta$	$\tan \theta$	$\csc \theta$	$\sec \theta$	$\cot \theta$
…
$\pi /6$	$\frac{1}{2}$	$\frac{1}{2}\sqrt{3}$	$\frac{1}{3}\sqrt{3}$	$2$	$\frac{2}{3}\sqrt{3}$	$\sqrt{3}$
$\pi /4$	$\frac{1}{2}\sqrt{2}$	$\frac{1}{2}\sqrt{2}$	$1$	$\sqrt{2}$	$\sqrt{2}$	$1$
$\pi /3$	$\frac{1}{2}\sqrt{3}$	$\frac{1}{2}$	$\sqrt{3}$	$\frac{2}{3}\sqrt{3}$	$2$	$\frac{1}{3}\sqrt{3}$
…
$\pi /2$	1	0	$\mathrm{\infty }$	1	$\mathrm{\infty }$	0
…
$2\pi /3$	$\frac{1}{2}\sqrt{3}$	$-\frac{1}{2}$	$-\sqrt{3}$	$\frac{2}{3}\sqrt{3}$	$-2$	$-\frac{1}{3}\sqrt{3}$
…

►

…

18: 17.7 Special Cases of Higher ${}_r{}^{}\varphi _s^{}$ Functions

… ►

17.7.5 $${}_3{}^{}\varphi _2^{}(\genfrac{}{}{0pt}{}{a,b,c}{e,f};q,q)+\frac{{(q/e,a,b,c,qf/e;q)}_{\mathrm{\infty }}}{{(e/q,aq/e,bq/e,cq/e,f;q)}_{\mathrm{\infty }}}{}_3{}^{}\varphi _2^{}(\genfrac{}{}{0pt}{}{aq/e,bq/e,cq/e}{q^2/e,qf/e};q,q)=\frac{{(q/e,f/a,f/b,f/c;q)}_{\mathrm{\infty }}}{{(aq/e,bq/e,cq/e,f;q)}_{\mathrm{\infty }}},$$

ⓘ

Symbols:

${}_{r+1}{}^{}\varphi _s^{}(a_0,\mathrm{\dots },a_r;b_1,\mathrm{\dots },b_s;q,z)$ or ${}_{r+1}{}^{}\varphi _s^{}(\genfrac{}{}{0pt}{}{a_0,\mathrm{\dots },a_r}{b_1,\mathrm{\dots },b_s};q,z)$: basic hypergeometric (or $q$-hypergeometric) function, ${(a_1,a_2,\mathrm{\dots },a_r;q)}_n$: multiple $q$-Pochhammer symbol and $q$: complex base

Permalink:

http://dlmf.nist.gov/17.7.E5

Encodings:

pMML, png, TeX

See also:

Annotations for §17.7(ii), §17.7(ii), §17.7 and Ch.17

… ►where $\lambda =-c{(ab/q)}^{\frac{1}{2}}$. … ►

17.7.14 $${}_8{}^{}\varphi _7^{}(\genfrac{}{}{0pt}{}{a,q{a}^{\frac{1}{2}},-q{a}^{\frac{1}{2}},b,c,d,e,q^{-n}}{a^{\frac{1}{2}},-a^{\frac{1}{2}},aq/b,aq/c,aq/d,aq/e,a{q}^{n+1}};q,q)=\frac{{(aq,aq/(bc),aq/(bd),aq/(cd);q)}_n}{{(aq/b,aq/c,aq/d,aq/(bcd);q)}_n},$$

ⓘ

Symbols:

${}_{r+1}{}^{}\varphi _s^{}(a_0,\mathrm{\dots },a_r;b_1,\mathrm{\dots },b_s;q,z)$ or ${}_{r+1}{}^{}\varphi _s^{}(\genfrac{}{}{0pt}{}{a_0,\mathrm{\dots },a_r}{b_1,\mathrm{\dots },b_s};q,z)$: basic hypergeometric (or $q$-hypergeometric) function, ${(a_1,a_2,\mathrm{\dots },a_r;q)}_n$: multiple $q$-Pochhammer symbol, $q$: complex base and $n$: nonnegative integer

Referenced by:

§17.7(iii)

Permalink:

http://dlmf.nist.gov/17.7.E14

Encodings:

pMML, png, TeX

See also:

Annotations for §17.7(iii), §17.7(iii), §17.7 and Ch.17

… ►

17.7.15 $${}_6{}^{}\varphi _5^{}(\genfrac{}{}{0pt}{}{a,q{a}^{\frac{1}{2}},-q{a}^{\frac{1}{2}},b,c,d}{a^{\frac{1}{2}},-a^{\frac{1}{2}},aq/b,aq/c,aq/d};q,\frac{aq}{bcd})=\frac{{(aq,aq/(bc),aq/(bd),aq/(cd);q)}_{\mathrm{\infty }}}{{(aq/b,aq/c,aq/d,aq/(bcd);q)}_{\mathrm{\infty }}},$$

ⓘ

Symbols:

${}_{r+1}{}^{}\varphi _s^{}(a_0,\mathrm{\dots },a_r;b_1,\mathrm{\dots },b_s;q,z)$ or ${}_{r+1}{}^{}\varphi _s^{}(\genfrac{}{}{0pt}{}{a_0,\mathrm{\dots },a_r}{b_1,\mathrm{\dots },b_s};q,z)$: basic hypergeometric (or $q$-hypergeometric) function, ${(a_1,a_2,\mathrm{\dots },a_r;q)}_n$: multiple $q$-Pochhammer symbol and $q$: complex base

Permalink:

http://dlmf.nist.gov/17.7.E15

Encodings:

pMML, png, TeX

See also:

Annotations for §17.7(iii), §17.7(iii), §17.7 and Ch.17

… ►

17.7.17 $${}_8{}^{}\varphi _7^{}(\genfrac{}{}{0pt}{}{a,q{a}^{\frac{1}{2}},-q{a}^{\frac{1}{2}},b,c,d,e,f}{a^{\frac{1}{2}},-a^{\frac{1}{2}},aq/b,aq/c,aq/d,aq/e,aq/f};q,q)-\frac{b}{a}\frac{{(aq,c,d,e,f,bq/a,bq/c,bq/d,bq/e,bq/f;q)}_{\mathrm{\infty }}}{{(aq/b,aq/c,aq/d,aq/e,aq/f,bc/a,bd/a,be/a,bf/a,b^{2}q/a;q)}_{\mathrm{\infty }}}{}_8{}^{}\varphi _7^{}(\genfrac{}{}{0pt}{}{b^2/a,qb{a}^{-\frac{1}{2}},-qb{a}^{-\frac{1}{2}},b,bc/a,bd/a,be/a,bf/a}{b{a}^{-\frac{1}{2}},-b{a}^{-\frac{1}{2}},bq/a,bq/c,bq/d,bq/e,bq/f};q,q)=\frac{{(aq,b/a,aq/(cd),aq/(ce),aq/(cf),aq/(de),aq/(df),aq/(ef);q)}_{\mathrm{\infty }}}{{(aq/c,aq/d,aq/e,aq/f,bc/a,bd/a,be/a,bf/a;q)}_{\mathrm{\infty }}},$$

ⓘ

Symbols:

${}_{r+1}{}^{}\varphi _s^{}(a_0,\mathrm{\dots },a_r;b_1,\mathrm{\dots },b_s;q,z)$ or ${}_{r+1}{}^{}\varphi _s^{}(\genfrac{}{}{0pt}{}{a_0,\mathrm{\dots },a_r}{b_1,\mathrm{\dots },b_s};q,z)$: basic hypergeometric (or $q$-hypergeometric) function, ${(a_1,a_2,\mathrm{\dots },a_r;q)}_n$: multiple $q$-Pochhammer symbol and $q$: complex base

Permalink:

http://dlmf.nist.gov/17.7.E17

Encodings:

pMML, png, TeX

See also:

Annotations for §17.7(iii), §17.7(iii), §17.7 and Ch.17

…

19: 9.10 Integrals

… ►

9.10.4 $${\int }_x^{\mathrm{\infty }}\mathrm{Ai}\left(t\right)dt\sim \frac{1}{2}{\pi }^{-1/2}{x}^{-3/4}\exp \left(-\frac{2}{3}{x}^{3/2}\right),$$ $x\to \mathrm{\infty }$,

ⓘ

Symbols:

$\mathrm{Ai}\left(z\right)$: Airy function, $\sim$: asymptotic equality, $\pi$: the ratio of the circumference of a circle to its diameter, $dx$: differential of $x$ , $\exp z$: exponential function, $\int$: integral and $x$: real variable

Proof sketch:

Integrate the leading term of (9.7.5).

Referenced by:

§9.10(ii)

Permalink:

http://dlmf.nist.gov/9.10.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §9.10(ii), §9.10 and Ch.9

… ►

9.10.6 $${\int }_{-\mathrm{\infty }}^x\mathrm{Ai}\left(t\right)dt={\pi }^{-1/2}{(-x)}^{-3/4}\cos \left(\frac{2}{3}{(-x)}^{3/2}+\frac{1}{4}\pi \right)+O\left({|x|}^{-9/4}\right),$$ $x\to -\mathrm{\infty }$,

ⓘ

Symbols:

$\mathrm{Ai}\left(z\right)$: Airy function, $O\left(x\right)$: order not exceeding, $\pi$: the ratio of the circumference of a circle to its diameter, $\cos z$: cosine function, $dx$: differential of $x$ , $\int$: integral and $x$: real variable

Proof sketch:

Integrate the leading terms of (9.7.5) and use (9.10.11)

Permalink:

http://dlmf.nist.gov/9.10.E6

Encodings:

pMML, png, TeX

See also:

Annotations for §9.10(ii), §9.10 and Ch.9

►

9.10.7 $${\int }_{-\mathrm{\infty }}^x\mathrm{Bi}\left(t\right)dt={\pi }^{-1/2}{(-x)}^{-3/4}\sin \left(\frac{2}{3}{(-x)}^{3/2}+\frac{1}{4}\pi \right)+O\left({|x|}^{-9/4}\right),$$ $x\to -\mathrm{\infty }$.

ⓘ

Symbols:

$\mathrm{Bi}\left(z\right)$: Airy function, $O\left(x\right)$: order not exceeding, $\pi$: the ratio of the circumference of a circle to its diameter, $dx$: differential of $x$ , $\int$: integral, $\sin z$: sine function and $x$: real variable

Proof sketch:

Integrate the leading terms of (9.7.7) and use (9.10.12)

Referenced by:

§9.10(ii)

Permalink:

http://dlmf.nist.gov/9.10.E7

Encodings:

pMML, png, TeX

See also:

Annotations for §9.10(ii), §9.10 and Ch.9

… ►

9.10.18 $$\mathrm{Ai}\left(z\right)=\frac{3z^{5/4}{\mathrm{e}}^{-(2/3)z^{3/2}}}{4\pi }{\int }_0^{\mathrm{\infty }}\frac{t^{-3/4}{\mathrm{e}}^{-(2/3)t^{3/2}}\mathrm{Ai}\left(t\right)}{z^{3/2}+t^{3/2}}dt,$$ .

ⓘ

Symbols:

$\mathrm{Ai}\left(z\right)$: Airy function, $\pi$: the ratio of the circumference of a circle to its diameter, $dx$: differential of $x$ , $\mathrm{e}$: base of natural logarithm, $\int$: integral, $\mathrm{ph}$: phase and $z$: complex variable

Proof sketch:

To prove this equation, combine (13.4.5) with (13.6.11) and use (5.5.3).

Referenced by:

(9.10.19), §9.17(iii), §9.5(ii), Erratum (V1.0.10) for Equation (9.10.18)

Permalink:

http://dlmf.nist.gov/9.10.E18

Encodings:

pMML, png, TeX

Errata (effective with 1.0.10):

The original and incorrect version,

$$\mathrm{Ai}\left(z\right)=\frac{z^{5/4}{\mathrm{e}}^{-(2/3)z^{3/2}}}{2^{7/2}\pi }{\int }_0^{\mathrm{\infty }}\frac{t^{-1/2}{\mathrm{e}}^{-(2/3)t^{3/2}}\mathrm{Ai}\left(t\right)}{z^{3/2}+t^{3/2}}dt$$

taken from Schulten et al. (1979), has been corrected.

Reported 2015-03-20 by Walter Gautschi

See also:

Annotations for §9.10(vii), §9.10 and Ch.9

►

9.10.19 $$\mathrm{Bi}\left(x\right)=\frac{3x^{5/4}{\mathrm{e}}^{(2/3)x^{3/2}}}{2\pi }{⨍}_0^{\mathrm{\infty }}\frac{t^{-3/4}{\mathrm{e}}^{-(2/3)t^{3/2}}\mathrm{Ai}\left(t\right)}{x^{3/2}-t^{3/2}}dt,$$ $x>0$,

ⓘ

Symbols:

$\mathrm{Ai}\left(z\right)$: Airy function, $\mathrm{Bi}\left(z\right)$: Airy function, $\pi$: the ratio of the circumference of a circle to its diameter, $dx$: differential of $x$ , $\mathrm{e}$: base of natural logarithm, ${⨍}_a^b$: Cauchy principal value and $x$: real variable

Proof sketch:

To prove this equation, combine (9.2.10) with (9.10.18).

Referenced by:

§9.5(i), Erratum (V1.0.10) for Equation (9.10.19)

Permalink:

http://dlmf.nist.gov/9.10.E19

Encodings:

pMML, png, TeX

Errata (effective with 1.0.10):

The original and incorrect version,

$$\mathrm{Bi}\left(x\right)=\frac{x^{5/4}{\mathrm{e}}^{(2/3)x^{3/2}}}{2^{5/2}\pi }{⨍}_0^{\mathrm{\infty }}\frac{t^{-1/2}{\mathrm{e}}^{-(2/3)t^{3/2}}\mathrm{Ai}\left(t\right)}{x^{3/2}-t^{3/2}}dt$$

taken from Schulten et al. (1979), has been corrected.

Reported 2015-03-20 by Walter Gautschi

See also:

Annotations for §9.10(vii), §9.10 and Ch.9

…

20: 22.7 Landen Transformations

… ►

22.7.2 $$\mathrm{sn}(z,k)=\frac{(1+k_1)\mathrm{sn}(z/(1+k_1),k_1)}{1+k_1{\mathrm{sn}}^2(z/(1+k_1),k_1)},$$

ⓘ

Symbols:

$\mathrm{sn}(z,k)$: Jacobian elliptic function, $z$: complex, $k$: modulus and $k_1$: change of variable

A&S Ref:

16.12.2

Referenced by:

§22.20(iii)

Permalink:

http://dlmf.nist.gov/22.7.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §22.7(i), §22.7 and Ch.22

►

22.7.3 $$\mathrm{cn}(z,k)=\frac{\mathrm{cn}(z/(1+k_1),k_1)\mathrm{dn}(z/(1+k_1),k_1)}{1+k_1{\mathrm{sn}}^2(z/(1+k_1),k_1)},$$

ⓘ

Symbols:

$\mathrm{cn}(z,k)$: Jacobian elliptic function, $\mathrm{dn}(z,k)$: Jacobian elliptic function, $\mathrm{sn}(z,k)$: Jacobian elliptic function, $z$: complex, $k$: modulus and $k_1$: change of variable

A&S Ref:

16.12.3

Referenced by:

§22.20(iii)

Permalink:

http://dlmf.nist.gov/22.7.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §22.7(i), §22.7 and Ch.22

►

22.7.4 $$\mathrm{dn}(z,k)=\frac{{\mathrm{dn}}^2(z/(1+k_1),k_1)-(1-k_1)}{1+k_1-{\mathrm{dn}}^2(z/(1+k_1),k_1)}.$$

ⓘ

Symbols:

$\mathrm{dn}(z,k)$: Jacobian elliptic function, $z$: complex, $k$: modulus and $k_1$: change of variable

A&S Ref:

16.12.4

Referenced by:

§22.20(iii)

Permalink:

http://dlmf.nist.gov/22.7.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §22.7(i), §22.7 and Ch.22

… ►

22.7.6 $$\mathrm{sn}(z,k)=\frac{(1+k_2^{\prime })\mathrm{sn}(z/(1+k_2^{\prime }),k_2)\mathrm{cn}(z/(1+k_2^{\prime }),k_2)}{\mathrm{dn}(z/(1+k_2^{\prime }),k_2)},$$

ⓘ

Symbols:

$\mathrm{cn}(z,k)$: Jacobian elliptic function, $\mathrm{dn}(z,k)$: Jacobian elliptic function, $\mathrm{sn}(z,k)$: Jacobian elliptic function, $z$: complex, $k$: modulus, $k_2$: change of variable and $k_2^{\prime }$: change of variable

A&S Ref:

16.14.2

Permalink:

http://dlmf.nist.gov/22.7.E6

Encodings:

pMML, png, TeX

See also:

Annotations for §22.7(ii), §22.7 and Ch.22

… ►

22.7.8 $$\mathrm{dn}(z,k)=\frac{(1-k_2^{\prime })({\mathrm{dn}}^2(z/(1+k_2^{\prime }),k_2)+k_2^{\prime })}{k_2^2\mathrm{dn}(z/(1+k_2^{\prime }),k_2)}.$$

ⓘ

Symbols:

$\mathrm{dn}(z,k)$: Jacobian elliptic function, $z$: complex, $k$: modulus, $k_2$: change of variable and $k_2^{\prime }$: change of variable

A&S Ref:

16.14.4

Permalink:

http://dlmf.nist.gov/22.7.E8

Encodings:

pMML, png, TeX

See also:

Annotations for §22.7(ii), §22.7 and Ch.22

…