13 Confluent Hypergeometric Functions Kummer Functions 13.3 Recurrence Relations and Derivatives 13.5 Continued Fractions

§13.4 Integral Representations

Permalink:: http://dlmf.nist.gov/13.4

§13.4(i) Integrals Along the Real Line
§13.4(ii) Contour Integrals
§13.4(iii) Mellin–Barnes Integrals

§13.4(i) Integrals Along the Real Line

Notes:: See Buchholz (1969, §1.4), Erdélyi et al. (1953a, §6.11), and Slater (1960, Chapter 3). For (13.4.5) use (13.2.41); compare the proof of Lemma 3.1 in Olde Daalhuis and Olver (1994).
Keywords:: Kummer functions, hypergeometric function, integrals, integrals of Bessel and Hankel functions, integrals of modified Bessel functions
Referenced by:: §13.16(i)
Permalink:: http://dlmf.nist.gov/13.4.i

13.4.1 $\mathop{{\mathbf{M}}\/}\nolimits\!\left(a,b,z\right)=\frac{1}{\mathop{\Gamma\/% }\nolimits\!\left(a\right)\mathop{\Gamma\/}\nolimits\!\left(b-a\right)}\int_{{% 0}}^{{1}}e^{{zt}}t^{{a-1}}(1-t)^{{b-a-1}}dt,$ $\realpart{b}>\realpart{a}>0$ ,

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, $\mathop{{\mathbf{M}}\/}\nolimits\!\left(a,b,z\right)$ : Olver’s confluent hypergeometric function, : differential of , : base of exponential function, $\int$ : integral, $\realpart{}$ : real part and : complex variable
A&S Ref:: 13.2.1 (in different form)
Referenced by:: §13.10(v), §13.29(iii)
Permalink:: http://dlmf.nist.gov/13.4.E1
Encodings:: TeX, pMML, png

13.4.2 $\mathop{{\mathbf{M}}\/}\nolimits\!\left(a,b,z\right)=\frac{1}{\mathop{\Gamma\/% }\nolimits\!\left(b-c\right)}\int_{{0}}^{{1}}\mathop{{\mathbf{M}}\/}\nolimits% \!\left(a,c,zt\right)t^{{c-1}}(1-t)^{{b-c-1}}dt,$ $\realpart{b}>\realpart{c}>0$ ,

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, $\mathop{{\mathbf{M}}\/}\nolimits\!\left(a,b,z\right)$ : Olver’s confluent hypergeometric function, : differential of , $\int$ : integral, $\realpart{}$ : real part, : complex variable and : arbitrary
Referenced by:: §13.10(vi)
Permalink:: http://dlmf.nist.gov/13.4.E2
Encodings:: TeX, pMML, png

13.4.3 $\mathop{{\mathbf{M}}\/}\nolimits\!\left(a,b,-z\right)=\frac{z^{{\frac{1}{2}-% \frac{1}{2}b}}}{\mathop{\Gamma\/}\nolimits\!\left(a\right)}\int_{{0}}^{{\infty% }}e^{{-t}}t^{{a-\frac{1}{2}b-\frac{1}{2}}}\mathop{J_{{b-1}}\/}\nolimits\!\left% (2\sqrt{zt}\right)dt,$ $\realpart{a}>0$ .

Symbols:: $\mathop{J_{{\nu}}\/}\nolimits\!\left(z\right)$ : Bessel function of the first kind, $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, $\mathop{{\mathbf{M}}\/}\nolimits\!\left(a,b,z\right)$ : Olver’s confluent hypergeometric function, : differential of , : base of exponential function, $\int$ : integral, $\realpart{}$ : real part and : complex variable
Referenced by:: §13.10(v)
Permalink:: http://dlmf.nist.gov/13.4.E3
Encodings:: TeX, pMML, png

For the function $\mathop{J_{{b-1}}\/}\nolimits$ see §10.2(ii).

13.4.4 $\mathop{U\/}\nolimits\!\left(a,b,z\right)=\frac{1}{\mathop{\Gamma\/}\nolimits% \!\left(a\right)}\int_{{0}}^{{\infty}}e^{{-zt}}t^{{a-1}}(1+t)^{{b-a-1}}dt,$ $\realpart{a}>0$ , $|\mathop{\mathrm{ph}\/}\nolimits{z}|<\frac{1}{2}\pi$ ,

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, $\mathop{U\/}\nolimits\!\left(a,b,z\right)$ : Kummer confluent hypergeometric function, : differential of , : base of exponential function, $\int$ : integral, $\mathop{\mathrm{ph}\/}\nolimits$ : phase, $\realpart{}$ : real part and : complex variable
A&S Ref:: 13.2.5
Referenced by:: §13.10(v), §13.29(iii), §7.11
Permalink:: http://dlmf.nist.gov/13.4.E4
Encodings:: TeX, pMML, png

13.4.5 $\mathop{U\/}\nolimits\!\left(a,b,z\right)=\frac{z^{{1-a}}}{\mathop{\Gamma\/}% \nolimits\!\left(a\right)\mathop{\Gamma\/}\nolimits\!\left(1+a-b\right)}\int_{% {0}}^{{\infty}}\frac{\mathop{U\/}\nolimits\!\left(b-a,b,t\right)e^{{-t}}t^{{a-% 1}}}{t+z}dt,$ $|\mathop{\mathrm{ph}\/}\nolimits{z}|<\pi$ , $\realpart{a}>\max\left(\realpart{b-1},0\right)$ ,

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, $\mathop{U\/}\nolimits\!\left(a,b,z\right)$ : Kummer confluent hypergeometric function, : differential of , : base of exponential function, $\int$ : integral, : open interval, $\mathop{\mathrm{ph}\/}\nolimits$ : phase, $\realpart{}$ : real part and : complex variable
Referenced by:: §13.10(vi), §13.4(i)
Permalink:: http://dlmf.nist.gov/13.4.E5
Encodings:: TeX, pMML, png

13.4.6 $\mathop{U\/}\nolimits\!\left(a,b,z\right)=\frac{(-1)^{n}z^{{1-b-n}}}{\mathop{% \Gamma\/}\nolimits\!\left(1+a-b\right)}\int_{0}^{\infty}\frac{\mathop{{\mathbf% {M}}\/}\nolimits\!\left(b-a,b,t\right)e^{{-t}}t^{{b+n-1}}}{t+z}dt,$ $\left|\mathop{\mathrm{ph}\/}\nolimits z\right|<\pi$ , $n=0,1,2,\dots$ , $-\realpart{b}<n<1+\realpart{(a-b)}$ ,

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, $\mathop{U\/}\nolimits\!\left(a,b,z\right)$ : Kummer confluent hypergeometric function, $\mathop{{\mathbf{M}}\/}\nolimits\!\left(a,b,z\right)$ : Olver’s confluent hypergeometric function, : differential of , : base of exponential function, $\int$ : integral, $\mathop{\mathrm{ph}\/}\nolimits$ : phase, $\realpart{}$ : real part, : nonnegative integer and : complex variable
Referenced by:: §13.10(vi)
Permalink:: http://dlmf.nist.gov/13.4.E6
Encodings:: TeX, pMML, png

13.4.7 $\mathop{U\/}\nolimits\!\left(a,b,z\right)=\frac{2z^{{\frac{1}{2}-\frac{1}{2}b}% }}{\mathop{\Gamma\/}\nolimits\!\left(a\right)\mathop{\Gamma\/}\nolimits\!\left% (a-b+1\right)}\*\int_{{0}}^{{\infty}}e^{{-t}}t^{{a-\frac{1}{2}b-\frac{1}{2}}}% \mathop{K_{{b-1}}\/}\nolimits\!\left(2\sqrt{zt}\right)dt,$ $\realpart{a}>\max\left(\realpart{b-1},0\right)$ ,

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, $\mathop{U\/}\nolimits\!\left(a,b,z\right)$ : Kummer confluent hypergeometric function, : differential of , : base of exponential function, $\int$ : integral, $\mathop{K_{{\nu}}\/}\nolimits\!\left(z\right)$ : modified Bessel function, : open interval, $\realpart{}$ : real part and : complex variable
Permalink:: http://dlmf.nist.gov/13.4.E7
Encodings:: TeX, pMML, png

13.4.8 $\mathop{U\/}\nolimits\!\left(a,b,z\right)=z^{{c-a}}\*\int_{{0}}^{{\infty}}e^{{% -zt}}t^{{c-1}}\mathop{{{}_{{2}}{\mathbf{F}}_{{1}}}\/}\nolimits\!\left(a,a-b+1;% c;-t\right)dt,$ $|\mathop{\mathrm{ph}\/}\nolimits{z}|<\frac{1}{2}\pi$ ,

Symbols:: $\mathop{U\/}\nolimits\!\left(a,b,z\right)$ : Kummer confluent hypergeometric function, : differential of , : base of exponential function, $\mathop{{{}_{{p}}{\mathbf{F}}_{{q}}}\/}\nolimits\!\left({\mathbf{a}\atop% \mathbf{b}};z\right)$ : scaled (or Olver’s) generalized hypergeometric function, $\int$ : integral, $\mathop{\mathrm{ph}\/}\nolimits$ : phase, : complex variable and : arbitrary
Permalink:: http://dlmf.nist.gov/13.4.E8
Encodings:: TeX, pMML, png

where is arbitrary, $\realpart{c}>0$ . For the functions $\mathop{K_{{b-1}}\/}\nolimits$ and $\mathop{{{}_{{2}}{\mathbf{F}}_{{1}}}\/}\nolimits$ see §10.25(ii) and §§15.1, 15.2(i).

§13.4(ii) Contour Integrals

Notes:: See Buchholz (1969, §1.4), Erdélyi et al. (1953a, §6.11), and Slater (1960, Chapter 3).
Keywords:: Kummer functions, hypergeometric function, integrals
Referenced by:: §13.16(ii)
Permalink:: http://dlmf.nist.gov/13.4.ii

13.4.9 $\mathop{{\mathbf{M}}\/}\nolimits\!\left(a,b,z\right)=\frac{\mathop{\Gamma\/}% \nolimits\!\left(1+a-b\right)}{2\pi i\mathop{\Gamma\/}\nolimits\!\left(a\right% )}\int_{0}^{{(1+)}}e^{{zt}}t^{{a-1}}{(t-1)^{{b-a-1}}}dt,$ $b-a\neq 1,2,3,\dots$ , $\realpart{a}>0$ .

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, $\mathop{{\mathbf{M}}\/}\nolimits\!\left(a,b,z\right)$ : Olver’s confluent hypergeometric function, : differential of , : base of exponential function, $\int$ : integral, $\realpart{}$ : real part and : complex variable
Permalink:: http://dlmf.nist.gov/13.4.E9
Encodings:: TeX, pMML, png

13.4.10 $\mathop{{\mathbf{M}}\/}\nolimits\!\left(a,b,z\right)=e^{{-a\pi i}}\frac{% \mathop{\Gamma\/}\nolimits\!\left(1-a\right)}{2\pi i\mathop{\Gamma\/}\nolimits% \!\left(b-a\right)}\int_{1}^{{(0+)}}e^{{zt}}t^{{a-1}}{(1-t)^{{b-a-1}}}dt,$ $a\neq 1,2,3,\dots$ , $\realpart{(b-a)}>0$ .

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, $\mathop{{\mathbf{M}}\/}\nolimits\!\left(a,b,z\right)$ : Olver’s confluent hypergeometric function, : differential of , : base of exponential function, $\int$ : integral, $\realpart{}$ : real part and : complex variable
Referenced by:: §13.8(i)
Permalink:: http://dlmf.nist.gov/13.4.E10
Encodings:: TeX, pMML, png

Figure 13.4.1: Contour of integration in (13.4.11). (Compare Figure 5.12.3.)

Keywords:: Pochhammer double-loop contour
Referenced by:: §13.4(ii)
Permalink:: http://dlmf.nist.gov/13.4.F1
Encodings:: pdf, png

13.4.11 $\mathop{{\mathbf{M}}\/}\nolimits\!\left(a,b,z\right)=e^{{-b\pi i}}\mathop{% \Gamma\/}\nolimits\!\left(1-a\right)\mathop{\Gamma\/}\nolimits\!\left(1+a-b% \right)\*\frac{1}{4\pi^{2}}\int_{{\alpha}}^{{(0+,1+,0-,1-)}}e^{{zt}}t^{{a-1}}{% (1-t)^{{b-a-1}}}dt,$ $a,b-a\neq 1,2,3,\dots$ .

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, $\mathop{{\mathbf{M}}\/}\nolimits\!\left(a,b,z\right)$ : Olver’s confluent hypergeometric function, : differential of , : base of exponential function, $\int$ : integral and : complex variable
Referenced by:: Figure 13.4.1, Figure 13.4.1
Permalink:: http://dlmf.nist.gov/13.4.E11
Encodings:: TeX, pMML, png

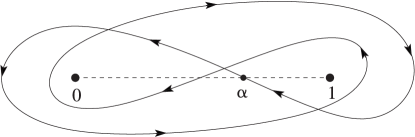
The contour of integration starts and terminates at a point $\alpha$ on the real axis between 0 and 1. It encircles and once in the positive sense, and then once in the negative sense. See Figure 13.4.1. The fractional powers are continuous and assume their principal values at $t=\alpha$ . Similar conventions also apply to the remaining integrals in this subsection.

13.4.12 $\mathop{{\mathbf{M}}\/}\nolimits\!\left(a,c,z\right)=\frac{\mathop{\Gamma\/}% \nolimits\!\left(b\right)}{2\pi i}z^{{1-b}}\int_{{-\infty}}^{{(0+,1+)}}e^{{zt}% }t^{{-b}}\mathop{{{}_{{2}}{\mathbf{F}}_{{1}}}\/}\nolimits\!\left(a,b;c;\ifrac{% 1}{t}\right)dt,$ $b\neq 0,-1,-2,\dots$ , $\left|\mathop{\mathrm{ph}\/}\nolimits z\right|<\frac{1}{2}\pi$ .

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, $\mathop{{\mathbf{M}}\/}\nolimits\!\left(a,b,z\right)$ : Olver’s confluent hypergeometric function, : differential of , : base of exponential function, $\mathop{{{}_{{p}}{\mathbf{F}}_{{q}}}\/}\nolimits\!\left({\mathbf{a}\atop% \mathbf{b}};z\right)$ : scaled (or Olver’s) generalized hypergeometric function, $\int$ : integral, : open interval, $\mathop{\mathrm{ph}\/}\nolimits$ : phase and : complex variable
Permalink:: http://dlmf.nist.gov/13.4.E12
Encodings:: TeX, pMML, png

At the point where the contour crosses the interval $(1,\infty)$ , $t^{{-b}}$ and the $\mathop{{{}_{{2}}{\mathbf{F}}_{{1}}}\/}\nolimits$ function assume their principal values; compare §§15.1 and 15.2(i). A special case is

13.4.13 $\mathop{{\mathbf{M}}\/}\nolimits\!\left(a,b,z\right)=\frac{z^{{1-b}}}{2\pi i}% \int_{{-\infty}}^{{(0+,1+)}}e^{{zt}}t^{{-b}}\!\left(1-\frac{1}{t}\right)^{{-a}% }dt,$ $|\mathop{\mathrm{ph}\/}\nolimits{z}|<\frac{1}{2}\pi$ .

Symbols:: $\mathop{{\mathbf{M}}\/}\nolimits\!\left(a,b,z\right)$ : Olver’s confluent hypergeometric function, : differential of , : base of exponential function, $\int$ : integral, : open interval, $\mathop{\mathrm{ph}\/}\nolimits$ : phase and : complex variable
Permalink:: http://dlmf.nist.gov/13.4.E13
Encodings:: TeX, pMML, png

13.4.14 $\mathop{U\/}\nolimits\!\left(a,b,z\right)=e^{{-a\pi i}}\frac{\mathop{\Gamma\/}% \nolimits\!\left(1-a\right)}{2\pi i}\int_{{\infty}}^{{(0+)}}e^{{-zt}}t^{{a-1}}% {(1+t)^{{b-a-1}}}dt,$ $a\neq 1,2,3,\dots$ , $\left|\mathop{\mathrm{ph}\/}\nolimits z\right|<\frac{1}{2}\pi$ .

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, $\mathop{U\/}\nolimits\!\left(a,b,z\right)$ : Kummer confluent hypergeometric function, : differential of , : base of exponential function, $\int$ : integral, $\mathop{\mathrm{ph}\/}\nolimits$ : phase and : complex variable
Referenced by:: §13.20(i)
Permalink:: http://dlmf.nist.gov/13.4.E14
Encodings:: TeX, pMML, png

The contour cuts the real axis between −1 and 0. At this point the fractional powers are determined by $\mathop{\mathrm{ph}\/}\nolimits{t}=\pi$ and $\mathop{\mathrm{ph}\/}\nolimits(1+t)=0$ .

13.4.15 $\frac{\mathop{U\/}\nolimits\!\left(a,b,z\right)}{\mathop{\Gamma\/}\nolimits\!% \left(c\right)\mathop{\Gamma\/}\nolimits\!\left(c-b+1\right)}=\frac{z^{{1-c}}}% {2\pi i}\int_{{-\infty}}^{{(0+)}}e^{{zt}}t^{{-c}}\mathop{{{}_{{2}}{\mathbf{F}}% _{{1}}}\/}\nolimits\!\left(a,c;a+c-b+1;1-\frac{1}{t}\right)dt,$ $\left|\mathop{\mathrm{ph}\/}\nolimits z\right|<\frac{1}{2}\pi$ .

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, $\mathop{U\/}\nolimits\!\left(a,b,z\right)$ : Kummer confluent hypergeometric function, : differential of , : base of exponential function, $\mathop{{{}_{{p}}{\mathbf{F}}_{{q}}}\/}\nolimits\!\left({\mathbf{a}\atop% \mathbf{b}};z\right)$ : scaled (or Olver’s) generalized hypergeometric function, $\int$ : integral, $\mathop{\mathrm{ph}\/}\nolimits$ : phase and : complex variable
Permalink:: http://dlmf.nist.gov/13.4.E15
Encodings:: TeX, pMML, png

Again, $t^{{-c}}$ and the $\mathop{{{}_{{2}}{\mathbf{F}}_{{1}}}\/}\nolimits$ function assume their principal values where the contour intersects the positive real axis.

§13.4(iii) Mellin–Barnes Integrals

Notes:: Combine the results of Buchholz (1969, §5.4) with (13.14.2), (13.14.3).
Keywords:: Kummer functions
Permalink:: http://dlmf.nist.gov/13.4.iii

If $a\neq 0,-1,-2,\dots$ , then

13.4.16 $\mathop{{\mathbf{M}}\/}\nolimits\!\left(a,b,-z\right)=\frac{1}{2\pi i\mathop{% \Gamma\/}\nolimits\!\left(a\right)}\int_{{-i\infty}}^{{i\infty}}\frac{\mathop{% \Gamma\/}\nolimits\!\left(a+t\right)\mathop{\Gamma\/}\nolimits\!\left(-t\right% )}{\mathop{\Gamma\/}\nolimits\!\left(b+t\right)}z^{{t}}dt,$ $|\mathop{\mathrm{ph}\/}\nolimits{z}|<\tfrac{1}{2}\pi$ ,

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, $\mathop{{\mathbf{M}}\/}\nolimits\!\left(a,b,z\right)$ : Olver’s confluent hypergeometric function, : differential of , $\int$ : integral, $\mathop{\mathrm{ph}\/}\nolimits$ : phase and : complex variable
A&S Ref:: 13.2.9 (in different form)
Permalink:: http://dlmf.nist.gov/13.4.E16
Encodings:: TeX, pMML, png

where the contour of integration separates the poles of $\mathop{\Gamma\/}\nolimits\!\left(a+t\right)$ from those of $\mathop{\Gamma\/}\nolimits\!\left(-t\right)$ .

If and $a-b+1\neq 0,-1,-2,\dots$ , then

13.4.17 $\mathop{U\/}\nolimits\!\left(a,b,z\right)=\frac{z^{{-a}}}{2\pi i}\int_{{-i% \infty}}^{{i\infty}}\frac{\mathop{\Gamma\/}\nolimits\!\left(a+t\right)\mathop{% \Gamma\/}\nolimits\!\left(1+a-b+t\right)\mathop{\Gamma\/}\nolimits\!\left(-t% \right)}{\mathop{\Gamma\/}\nolimits\!\left(a\right)\mathop{\Gamma\/}\nolimits% \!\left(1+a-b\right)}z^{{-t}}dt,$ $|\mathop{\mathrm{ph}\/}\nolimits{z}|<\tfrac{3}{2}\pi$ ,

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, $\mathop{U\/}\nolimits\!\left(a,b,z\right)$ : Kummer confluent hypergeometric function, : differential of , $\int$ : integral, $\mathop{\mathrm{ph}\/}\nolimits$ : phase and : complex variable
A&S Ref:: 13.2.10
Referenced by:: §13.6(vi)
Permalink:: http://dlmf.nist.gov/13.4.E17
Encodings:: TeX, pMML, png

where the contour of integration separates the poles of $\mathop{\Gamma\/}\nolimits\!\left(a+t\right)\mathop{\Gamma\/}\nolimits\!\left(% 1+a-b+t\right)$ from those of $\mathop{\Gamma\/}\nolimits\!\left(-t\right)$ .

13.4.18 $\mathop{U\/}\nolimits\!\left(a,b,z\right)=\frac{z^{{1-b}}e^{{z}}}{2\pi i}\int_% {{-i\infty}}^{{i\infty}}\frac{\mathop{\Gamma\/}\nolimits\!\left(b-1+t\right)% \mathop{\Gamma\/}\nolimits\!\left(t\right)}{\mathop{\Gamma\/}\nolimits\!\left(% a+t\right)}z^{{-t}}dt,$ $|\mathop{\mathrm{ph}\/}\nolimits{z}|<\tfrac{1}{2}\pi$ ,

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, $\mathop{U\/}\nolimits\!\left(a,b,z\right)$ : Kummer confluent hypergeometric function, : differential of , : base of exponential function, $\int$ : integral, $\mathop{\mathrm{ph}\/}\nolimits$ : phase and : complex variable
Permalink:: http://dlmf.nist.gov/13.4.E18
Encodings:: TeX, pMML, png

where the contour of integration passes all the poles of $\mathop{\Gamma\/}\nolimits\!\left(b-1+t\right)\mathop{\Gamma\/}\nolimits\!% \left(t\right)$ on the right-hand side.

© 2010–2013 NIST / Privacy Policy / Disclaimer / Feedback; Version 1.0.6; Release date 2013-05-06 Math-Image version (See MathML) . A Printed Companionis available. 13.3 Recurrence Relations and Derivatives 13.5 Continued Fractions

§13.4 Integral Representations

Contents

§13.4(i) Integrals Along the Real Line

§13.4(ii) Contour Integrals

§13.4(iii) Mellin–Barnes Integrals