8 Incomplete Gamma and Related Functions Related Functions 8.18 Asymptotic Expansions of $\mathop{I_{{x}}\/}\nolimits\!\left(a,b\right)$ 8.20 Asymptotic Expansions of $\mathop{E_{{p}}\/}\nolimits\!\left(z\right)$

§8.19 Generalized Exponential Integral

Keywords:: exponential integrals, generalized exponential integral
Permalink:: http://dlmf.nist.gov/8.19

§8.19(i) Definition and Integral Representations
§8.19(ii) Graphics
§8.19(iii) Special Values
§8.19(iv) Series Expansions
§8.19(v) Recurrence Relation and Derivatives
§8.19(vi) Relation to Confluent Hypergeometric Function
§8.19(vii) Continued Fraction
§8.19(viii) Analytic Continuation
§8.19(ix) Inequalities
§8.19(x) Integrals
§8.19(xi) Further Generalizations

§8.19(i) Definition and Integral Representations

Notes:: See Temme (1996b, p. 180).
Keywords:: generalized exponential integral, incomplete gamma functions, principal values
Referenced by:: §13.6(ii), §2.11(ii), ¶ ‣ §7.11, §8.4, §8.8
Permalink:: http://dlmf.nist.gov/8.19.i

For $p,z\in\Complex$

8.19.1 $\mathop{E_{{p}}\/}\nolimits\!\left(z\right)=z^{{p-1}}\mathop{\Gamma\/}% \nolimits\!\left(1-p,z\right).$

Defines:: $\mathop{E_{{p}}\/}\nolimits\!\left(z\right)$ : generalized exponential integral
Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(a,z\right)$ : incomplete gamma function, : complex variable and : parameter
A&S Ref:: 5.1.45 6.5.9 (Definition extended to general values of .)
Referenced by:: ¶ ‣ §8.19(i), §8.19(iii), §8.19(iv), §8.19(v), §8.19(vi), §8.19(vii)
Permalink:: http://dlmf.nist.gov/8.19.E1
Encodings:: TeX, pMML, png

Most properties of $\mathop{E_{{p}}\/}\nolimits\!\left(z\right)$ follow straightforwardly from those of $\mathop{\Gamma\/}\nolimits\!\left(a,z\right)$ . For an extensive treatment of $\mathop{E_{{1}}\/}\nolimits\!\left(z\right)$ see Chapter 6.

8.19.2 $\mathop{E_{{p}}\/}\nolimits\!\left(z\right)=z^{{p-1}}\int_{z}^{\infty}\frac{e^% {{-t}}}{t^{p}}dt.$

Symbols:: : differential of , : base of exponential function, $\mathop{E_{{p}}\/}\nolimits\!\left(z\right)$ : generalized exponential integral, $\int$ : integral, : complex variable and : parameter
Referenced by:: §8.19(i), §8.19(viii)
Permalink:: http://dlmf.nist.gov/8.19.E2
Encodings:: TeX, pMML, png

When the path of integration excludes the origin and does not cross the negative real axis (8.19.2) defines the principal value of $\mathop{E_{{p}}\/}\nolimits\!\left(z\right)$ , and unless indicated otherwise in the DLMF principal values are assumed.

¶ Other Integral Representations

Keywords:: generalized exponential integral

8.19.3 $\mathop{E_{{p}}\/}\nolimits\!\left(z\right)=\int_{1}^{\infty}\frac{e^{{-zt}}}{% t^{p}}dt,$ $|\mathop{\mathrm{ph}\/}\nolimits z|<\tfrac{1}{2}\pi$ ,

Symbols:: : differential of , : base of exponential function, $\mathop{E_{{p}}\/}\nolimits\!\left(z\right)$ : generalized exponential integral, $\int$ : integral, $\mathop{\mathrm{ph}\/}\nolimits$ : phase, : complex variable and : parameter
A&S Ref:: 5.1.4
Referenced by:: §8.19(iii)
Permalink:: http://dlmf.nist.gov/8.19.E3
Encodings:: TeX, pMML, png

8.19.4 $\mathop{E_{{p}}\/}\nolimits\!\left(z\right)=\frac{z^{{p-1}}e^{{-z}}}{\mathop{% \Gamma\/}\nolimits\!\left(p\right)}\int_{0}^{\infty}\frac{t^{{p-1}}e^{{-zt}}}{% 1+t}dt,$ $|\mathop{\mathrm{ph}\/}\nolimits z|<\tfrac{1}{2}\pi$ , $\realpart{p}>0$ .

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, : differential of , : base of exponential function, $\mathop{E_{{p}}\/}\nolimits\!\left(z\right)$ : generalized exponential integral, $\int$ : integral, $\mathop{\mathrm{ph}\/}\nolimits$ : phase, $\realpart{}$ : real part, : complex variable and : parameter
Permalink:: http://dlmf.nist.gov/8.19.E4
Encodings:: TeX, pMML, png

Integral representations of Mellin–Barnes type for $\mathop{E_{{p}}\/}\nolimits\!\left(z\right)$ follow immediately from (8.6.11), (8.6.12), and (8.19.1).

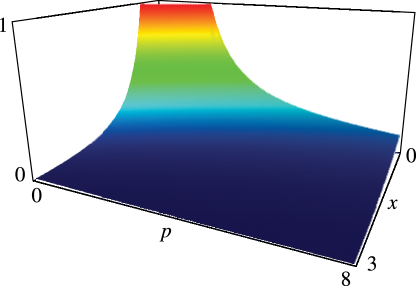
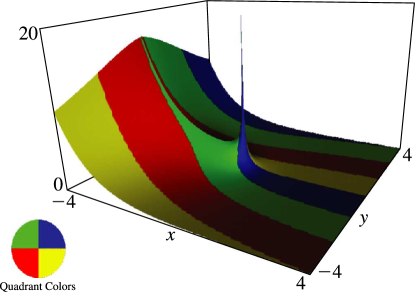
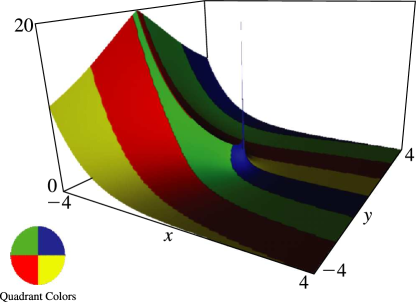
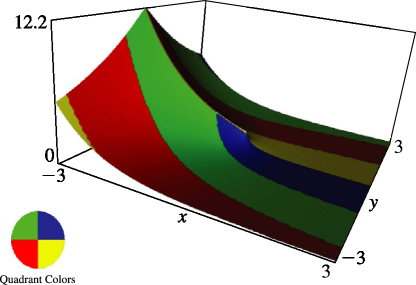
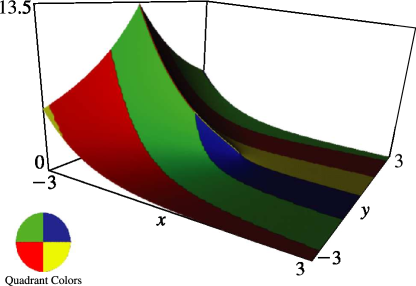
§8.19(ii) Graphics

Notes:: These graphics were produced at NIST.
Keywords:: generalized exponential integral
Permalink:: http://dlmf.nist.gov/8.19.ii

Visualization Help

Figure 8.19.1: $\mathop{E_{{p}}\/}\nolimits\!\left(x\right)$ , $0\leq x\leq 3$ , $0\leq p\leq 8$ .

Symbols:: $\mathop{E_{{p}}\/}\nolimits\!\left(z\right)$ : generalized exponential integral, : real variable and : parameter
Permalink:: http://dlmf.nist.gov/8.19.F1
Encodings:: VRML, X3D, pdf, png

In Figures 8.19.2–8.19.5, height corresponds to the absolute value of the function and color to the phase. See About Color Map.

Visualization Help

Figure 8.19.2: $\mathop{E_{{\frac{1}{2}}}\/}\nolimits\!\left(x+iy\right)$ , $-4\leq x\leq 4$ , $-4\leq y\leq 4$ . Principal value. There is a branch cut along the negative real axis.

Symbols:: $\mathop{E_{{p}}\/}\nolimits\!\left(z\right)$ : generalized exponential integral and : real variable
Referenced by:: §8.19(ii)
Permalink:: http://dlmf.nist.gov/8.19.F2
Encodings:: VRML, X3D, pdf, png

Visualization Help

Figure 8.19.3: $\mathop{E_{{1}}\/}\nolimits\!\left(x+iy\right)$ , $-4\leq x\leq 4$ , $-4\leq y\leq 4$ . Principal value. There is a branch cut along the negative real axis.

Symbols:: $\mathop{E_{{p}}\/}\nolimits\!\left(z\right)$ : generalized exponential integral and : real variable
Permalink:: http://dlmf.nist.gov/8.19.F3
Encodings:: VRML, X3D, pdf, png

Visualization Help

Figure 8.19.4: $\mathop{E_{{\frac{3}{2}}}\/}\nolimits\!\left(x+iy\right)$ , $-3\leq x\leq 3$ , $-3\leq y\leq 3$ . Principal value. There is a branch cut along the negative real axis.

Symbols:: $\mathop{E_{{p}}\/}\nolimits\!\left(z\right)$ : generalized exponential integral and : real variable
Permalink:: http://dlmf.nist.gov/8.19.F4
Encodings:: VRML, X3D, pdf, png

Visualization Help

Figure 8.19.5: $\mathop{E_{{2}}\/}\nolimits\!\left(x+iy\right)$ , $-3\leq x\leq 3$ , $-3\leq y\leq 3$ . Principal value. There is a branch cut along the negative real axis.

Symbols:: $\mathop{E_{{p}}\/}\nolimits\!\left(z\right)$ : generalized exponential integral and : real variable
Referenced by:: §8.19(ii)
Permalink:: http://dlmf.nist.gov/8.19.F5
Encodings:: VRML, X3D, pdf, png

§8.19(iii) Special Values

Notes:: Use (8.19.1), (8.19.3), and (8.4.15).
Keywords:: generalized exponential integral
Permalink:: http://dlmf.nist.gov/8.19.iii

8.19.5 $\mathop{E_{{0}}\/}\nolimits\!\left(z\right)=z^{{-1}}e^{{-z}},$ $z\neq 0$ ,

Symbols:: : base of exponential function, $\mathop{E_{{p}}\/}\nolimits\!\left(z\right)$ : generalized exponential integral and : complex variable
A&S Ref:: 5.1.24
Permalink:: http://dlmf.nist.gov/8.19.E5
Encodings:: TeX, pMML, png

8.19.6 $\mathop{E_{{p}}\/}\nolimits\!\left(0\right)=\frac{1}{p-1},$ $\realpart{p}>1$ ,

Symbols:: $\mathop{E_{{p}}\/}\nolimits\!\left(z\right)$ : generalized exponential integral, $\realpart{}$ : real part and : parameter
A&S Ref:: 5.1.23 (Extended to general values of .)
Permalink:: http://dlmf.nist.gov/8.19.E6
Encodings:: TeX, pMML, png

8.19.7 $\mathop{E_{{n}}\/}\nolimits\!\left(z\right)=\frac{(-z)^{{n-1}}}{(n-1)!}\mathop% {E_{1}\/}\nolimits\!\left(z\right)+\frac{e^{{-z}}}{(n-1)!}\sum_{{k=0}}^{{n-2}}% (n-k-2)!(-z)^{k},$ $n=2,3,\dots$ .

Symbols:: : base of exponential function, $\mathop{E_{1}\/}\nolimits\!\left(z\right)$ : exponential integral, $\mathop{E_{{p}}\/}\nolimits\!\left(z\right)$ : generalized exponential integral, : : factorial, : complex variable, : nonnegative integer and : nonnegative integer
Permalink:: http://dlmf.nist.gov/8.19.E7
Encodings:: TeX, pMML, png

§8.19(iv) Series Expansions

Notes:: (8.19.8) follows from (8.4.13) and (8.4.15). (8.19.9) follows from (6.6.3), (8.19.1), and (8.4.15). (8.19.10) and (8.19.11) follow from (8.19.1) and (8.7.3).
Keywords:: generalized exponential integral
Referenced by:: §8.25(i)
Permalink:: http://dlmf.nist.gov/8.19.iv

For $n=1,2,3,\dots$ ,

8.19.8 $\mathop{E_{{n}}\/}\nolimits\!\left(z\right)=\frac{(-z)^{{n-1}}}{(n-1)!}(% \mathop{\psi\/}\nolimits\!\left(n\right)-\mathop{\ln\/}\nolimits z)-\sum_{{% \substack{k=0\\ k\neq n-1}}}^{\infty}\frac{(-z)^{k}}{k!(1-n+k)},$

Symbols:: $\mathop{\psi\/}\nolimits\!\left(z\right)$ : psi (or digamma) function, $\mathop{E_{{p}}\/}\nolimits\!\left(z\right)$ : generalized exponential integral, : : factorial, $\mathop{\ln\/}\nolimits z$ : principal branch of logarithm function, : complex variable, : nonnegative integer and : nonnegative integer
A&S Ref:: 5.1.12
Referenced by:: §8.19(iv)
Permalink:: http://dlmf.nist.gov/8.19.E8
Encodings:: TeX, pMML, png

and

8.19.9 $\mathop{E_{{n}}\/}\nolimits\!\left(z\right)=\frac{(-1)^{n}z^{{n-1}}}{(n-1)!}% \mathop{\ln\/}\nolimits z+\frac{e^{{-z}}}{(n-1)!}\sum_{{k=1}}^{{n-1}}(-z)^{{k-% 1}}\mathop{\Gamma\/}\nolimits\!\left(n-k\right)+\frac{e^{{-z}}(-z)^{{n-1}}}{(n% -1)!}\sum_{{k=0}}^{\infty}\frac{z^{k}}{k!}\mathop{\psi\/}\nolimits\!\left(k+1% \right),$

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, $\mathop{\psi\/}\nolimits\!\left(z\right)$ : psi (or digamma) function, : base of exponential function, $\mathop{E_{{p}}\/}\nolimits\!\left(z\right)$ : generalized exponential integral, : : factorial, $\mathop{\ln\/}\nolimits z$ : principal branch of logarithm function, : complex variable, : nonnegative integer and : nonnegative integer
Referenced by:: §8.19(iv)
Permalink:: http://dlmf.nist.gov/8.19.E9
Encodings:: TeX, pMML, png

with $|\mathop{\mathrm{ph}\/}\nolimits z|\leq\pi$ in both equations. For $\mathop{\psi\/}\nolimits\!\left(x\right)$ see §5.2(i).

When $p\in\Complex$

8.19.10 $\mathop{E_{{p}}\/}\nolimits\!\left(z\right)=z^{{p-1}}\mathop{\Gamma\/}% \nolimits\!\left(1-p\right)-\sum_{{k=0}}^{\infty}\frac{(-z)^{k}}{k!(1-p+k)},$

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, $\mathop{E_{{p}}\/}\nolimits\!\left(z\right)$ : generalized exponential integral, : : factorial, : complex variable, : parameter and : nonnegative integer
Referenced by:: §8.19(iv)
Permalink:: http://dlmf.nist.gov/8.19.E10
Encodings:: TeX, pMML, png

8.19.11 $\mathop{E_{{p}}\/}\nolimits\!\left(z\right)=\mathop{\Gamma\/}\nolimits\!\left(% 1-p\right)\left(z^{{p-1}}-e^{{-z}}\sum_{{k=0}}^{\infty}\frac{z^{k}}{\mathop{% \Gamma\/}\nolimits\!\left(2-p+k\right)}\right),$

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, : base of exponential function, $\mathop{E_{{p}}\/}\nolimits\!\left(z\right)$ : generalized exponential integral, : complex variable, : parameter and : nonnegative integer
Referenced by:: §8.19(iv)
Permalink:: http://dlmf.nist.gov/8.19.E11
Encodings:: TeX, pMML, png

again with $|\mathop{\mathrm{ph}\/}\nolimits z|\leq\pi$ in both equations. The right-hand sides are replaced by their limiting forms when $p=1,2,3,\dots$ .

§8.19(v) Recurrence Relation and Derivatives

Notes:: Combine (8.19.1) with (8.8.2), (8.8.16), and (8.8.19).
Keywords:: derivatives, generalized exponential integral
Permalink:: http://dlmf.nist.gov/8.19.v

8.19.12 $p\mathop{E_{{p+1}}\/}\nolimits\!\left(z\right)+z\mathop{E_{{p}}\/}\nolimits\!% \left(z\right)=e^{{-z}}.$

Symbols:: : base of exponential function, $\mathop{E_{{p}}\/}\nolimits\!\left(z\right)$ : generalized exponential integral, : complex variable and : parameter
Permalink:: http://dlmf.nist.gov/8.19.E12
Encodings:: TeX, pMML, png

8.19.13 $\frac{d}{dz}\mathop{E_{{p}}\/}\nolimits\!\left(z\right)=-\mathop{E_{{p-1}}\/}% \nolimits\!\left(z\right),$

Symbols:: $\frac{df}{dx}$ : derivative of with respect to , $\mathop{E_{{p}}\/}\nolimits\!\left(z\right)$ : generalized exponential integral, : complex variable and : parameter
A&S Ref:: 5.1.36 (Extended to general values of .)
Referenced by:: §8.19(x)
Permalink:: http://dlmf.nist.gov/8.19.E13
Encodings:: TeX, pMML, png

8.19.14 $\frac{d}{dz}(e^{z}\mathop{E_{{p}}\/}\nolimits\!\left(z\right))=e^{z}\mathop{E_% {{p}}\/}\nolimits\!\left(z\right)\left(1+\frac{p-1}{z}\right)-\frac{1}{z}.$

Symbols:: $\frac{df}{dx}$ : derivative of with respect to , : base of exponential function, $\mathop{E_{{p}}\/}\nolimits\!\left(z\right)$ : generalized exponential integral, : complex variable and : parameter
Permalink:: http://dlmf.nist.gov/8.19.E14
Encodings:: TeX, pMML, png

¶ -Derivatives

For $j=1,2,3,\dots$ ,

8.19.15 $\frac{{\partial}^{j}\mathop{E_{{p}}\/}\nolimits\!\left(z\right)}{{\partial p}^% {j}}=(-1)^{j}\int_{1}^{\infty}(\mathop{\ln\/}\nolimits t)^{j}t^{{-p}}e^{{-zt}}dt,$ $\realpart{z}>0$ .

Symbols:: : differential of , : base of exponential function, $\mathop{E_{{p}}\/}\nolimits\!\left(z\right)$ : generalized exponential integral, $\int$ : integral, $\mathop{\ln\/}\nolimits z$ : principal branch of logarithm function, $\frac{\partial f}{\partial x}$ : partial derivative of with respect to , $\realpart{}$ : real part, : complex variable, : parameter and : numbers
Permalink:: http://dlmf.nist.gov/8.19.E15
Encodings:: TeX, pMML, png

For properties and numerical tables see Milgram (1985), and also (when ) MacLeod (2002b).

§8.19(vi) Relation to Confluent Hypergeometric Function

Notes:: Use (8.19.1) and (8.5.3).
Keywords:: confluent hypergeometric functions, generalized exponential integral
Permalink:: http://dlmf.nist.gov/8.19.vi

8.19.16 $\mathop{E_{{p}}\/}\nolimits\!\left(z\right)=z^{{p-1}}e^{{-z}}\mathop{U\/}% \nolimits\!\left(p,p,z\right).$

Symbols:: $\mathop{U\/}\nolimits\!\left(a,b,z\right)$ : Kummer confluent hypergeometric function, : base of exponential function, $\mathop{E_{{p}}\/}\nolimits\!\left(z\right)$ : generalized exponential integral, : complex variable and : parameter
Permalink:: http://dlmf.nist.gov/8.19.E16
Encodings:: TeX, pMML, png

For $\mathop{U\/}\nolimits\!\left(a,b,z\right)$ see §13.2(i).

§8.19(vii) Continued Fraction

Notes:: Combine (8.9.2) and (8.19.1).
Keywords:: generalized exponential integral
Referenced by:: ¶ ‣ §3.10(ii)
Permalink:: http://dlmf.nist.gov/8.19.vii

8.19.17 $\mathop{E_{{p}}\/}\nolimits\!\left(z\right)=e^{{-z}}\left(\cfrac{1}{z+\cfrac{p% }{1+\cfrac{1}{z+\cfrac{p+1}{1+\cfrac{2}{z+\cdots}}}}}\right),$ $|\mathop{\mathrm{ph}\/}\nolimits z|<\pi$ .

Symbols:: : base of exponential function, $\mathop{E_{{p}}\/}\nolimits\!\left(z\right)$ : generalized exponential integral, $\mathop{\mathrm{ph}\/}\nolimits$ : phase, : complex variable and : parameter
A&S Ref:: 5.1.22
Permalink:: http://dlmf.nist.gov/8.19.E17
Encodings:: TeX, pMML, png

See also Cuyt et al. (2008, pp. 277–285).

§8.19(viii) Analytic Continuation

Notes:: See Olver (1994b).
Keywords:: analytic continuation, generalized exponential integral
Permalink:: http://dlmf.nist.gov/8.19.viii

The general function $\mathop{E_{{p}}\/}\nolimits\!\left(z\right)$ is attained by extending the path in (8.19.2) across the negative real axis. Unless is a nonpositive integer, $\mathop{E_{{p}}\/}\nolimits\!\left(z\right)$ has a branch point at . For $z\neq 0$ each branch of $\mathop{E_{{p}}\/}\nolimits\!\left(z\right)$ is an entire function of .

8.19.18 $\mathop{E_{{p}}\/}\nolimits\!\left(ze^{{2m\pi i}}\right)=\frac{2\pi ie^{{mp\pi i% }}}{\mathop{\Gamma\/}\nolimits\!\left(p\right)}\frac{\mathop{\sin\/}\nolimits% \!\left(mp\pi\right)}{\mathop{\sin\/}\nolimits\!\left(p\pi\right)}z^{{p-1}}+% \mathop{E_{{p}}\/}\nolimits\!\left(z\right),$ $m\in\Integer$ , $z\neq 0$ .

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, $\in$ : element of, : base of exponential function, $\mathop{E_{{p}}\/}\nolimits\!\left(z\right)$ : generalized exponential integral, $\Integer$ : set of all integers, $\mathop{\sin\/}\nolimits z$ : sine function, : complex variable and : parameter
Referenced by:: §2.11(ii)
Permalink:: http://dlmf.nist.gov/8.19.E18
Encodings:: TeX, pMML, png

§8.19(ix) Inequalities

Notes:: See Hopf (1934, pp. 26–27).
Keywords:: generalized exponential integral, inequalities
Permalink:: http://dlmf.nist.gov/8.19.ix

For $n=1,2,3,\dots$ and ,

8.19.19 $\frac{n-1}{n}\mathop{E_{{n}}\/}\nolimits\!\left(x\right)<\mathop{E_{{n+1}}\/}% \nolimits\!\left(x\right)<\mathop{E_{{n}}\/}\nolimits\!\left(x\right),$

Symbols:: $\mathop{E_{{p}}\/}\nolimits\!\left(z\right)$ : generalized exponential integral, : real variable and : nonnegative integer
A&S Ref:: 5.1.17
Permalink:: http://dlmf.nist.gov/8.19.E19
Encodings:: TeX, pMML, png

8.19.20 $\left(\mathop{E_{{n}}\/}\nolimits\!\left(x\right)\right)^{2}<\mathop{E_{{n-1}}% \/}\nolimits\!\left(x\right)\mathop{E_{{n+1}}\/}\nolimits\!\left(x\right),$

Symbols:: $\mathop{E_{{p}}\/}\nolimits\!\left(z\right)$ : generalized exponential integral, : real variable and : nonnegative integer
A&S Ref:: 5.1.18
Permalink:: http://dlmf.nist.gov/8.19.E20
Encodings:: TeX, pMML, png

8.19.21 $\frac{1}{x+n}<e^{x}\mathop{E_{{n}}\/}\nolimits\!\left(x\right)\leq\frac{1}{x+n% -1},$

Symbols:: : base of exponential function, $\mathop{E_{{p}}\/}\nolimits\!\left(z\right)$ : generalized exponential integral, : real variable and : nonnegative integer
A&S Ref:: 5.1.19
Permalink:: http://dlmf.nist.gov/8.19.E21
Encodings:: TeX, pMML, png

8.19.22 $\frac{d}{dx}\frac{\mathop{E_{{n}}\/}\nolimits\!\left(x\right)}{\mathop{E_{{n-1% }}\/}\nolimits\!\left(x\right)}>0.$

Symbols:: $\frac{df}{dx}$ : derivative of with respect to , $\mathop{E_{{p}}\/}\nolimits\!\left(z\right)$ : generalized exponential integral, : real variable and : nonnegative integer
A&S Ref:: 5.1.21
Permalink:: http://dlmf.nist.gov/8.19.E22
Encodings:: TeX, pMML, png

§8.19(x) Integrals

Notes:: See Kourganoff (1952, Appendix 1). For (8.19.23) use (8.19.13).
Keywords:: generalized exponential integral, integrals
Permalink:: http://dlmf.nist.gov/8.19.x

8.19.23 $\int_{z}^{\infty}\mathop{E_{{p-1}}\/}\nolimits\!\left(t\right)dt=\mathop{E_{{p% }}\/}\nolimits\!\left(z\right),$ $|\mathop{\mathrm{ph}\/}\nolimits z|<\pi$ ,

Symbols:: : differential of , $\mathop{E_{{p}}\/}\nolimits\!\left(z\right)$ : generalized exponential integral, $\int$ : integral, $\mathop{\mathrm{ph}\/}\nolimits$ : phase, : complex variable and : parameter
Referenced by:: §8.19(x)
Permalink:: http://dlmf.nist.gov/8.19.E23
Encodings:: TeX, pMML, png

8.19.24 $\int_{0}^{\infty}e^{{-at}}\mathop{E_{{n}}\/}\nolimits\!\left(t\right)dt=\frac{% (-1)^{{n-1}}}{a^{n}}\left(\mathop{\ln\/}\nolimits\!\left(1+a\right)+\sum_{{k=1% }}^{{n-1}}\frac{(-1)^{k}a^{k}}{k}\right),$ $n=1,2,\dots$ , $\realpart{a}>-1$ ,

Symbols:: : differential of , : base of exponential function, $\mathop{E_{{p}}\/}\nolimits\!\left(z\right)$ : generalized exponential integral, $\int$ : integral, $\mathop{\ln\/}\nolimits z$ : principal branch of logarithm function, $\realpart{}$ : real part, : parameter, : nonnegative integer and : nonnegative integer
A&S Ref:: 5.1.34
Referenced by:: §8.19(x)
Permalink:: http://dlmf.nist.gov/8.19.E24
Encodings:: TeX, pMML, png

8.19.25 $\int_{0}^{\infty}e^{{-at}}t^{{b-1}}\mathop{E_{{p}}\/}\nolimits\!\left(t\right)% dt=\frac{\mathop{\Gamma\/}\nolimits\!\left(b\right)(1+a)^{{-b}}}{p+b-1}\*% \mathop{F\/}\nolimits\!\left(1,b;p+b;a/(1+a)\right),$ $\realpart{a}>-1$ , $\realpart{(p+b)}>1$ .

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, $\mathop{F\/}\nolimits\!\left(a,b;c;z\right)$ : hypergeometric function, : differential of , : base of exponential function, $\mathop{E_{{p}}\/}\nolimits\!\left(z\right)$ : generalized exponential integral, $\int$ : integral, $\realpart{}$ : real part, : parameter and : parameter
Permalink:: http://dlmf.nist.gov/8.19.E25
Encodings:: TeX, pMML, png

8.19.26 $\int_{0}^{\infty}\mathop{E_{{p}}\/}\nolimits\!\left(t\right)\mathop{E_{{q}}\/}% \nolimits\!\left(t\right)dt=\frac{L(p)+L(q)}{p+q-1},$

Symbols:: : differential of , $\mathop{E_{{p}}\/}\nolimits\!\left(z\right)$ : generalized exponential integral, $\int$ : integral, : parameter and : function
Permalink:: http://dlmf.nist.gov/8.19.E26
Encodings:: TeX, pMML, png

where

8.19.27 $L(p)=\int_{0}^{\infty}e^{{-t}}\mathop{E_{{p}}\/}\nolimits\!\left(t\right)dt=% \frac{1}{2p}\mathop{F\/}\nolimits\!\left(1,1;1+p;\tfrac{1}{2}\right),$

Symbols:: $\mathop{F\/}\nolimits\!\left(a,b;c;z\right)$ : hypergeometric function, : differential of , : base of exponential function, $\mathop{E_{{p}}\/}\nolimits\!\left(z\right)$ : generalized exponential integral, $\int$ : integral, : parameter and : function
Permalink:: http://dlmf.nist.gov/8.19.E27
Encodings:: TeX, pMML, png

For the hypergeometric function $\mathop{F\/}\nolimits\!\left(a,b;c;z\right)$ see §15.2(i). When $p=1,2,3,\dots$ , can also be evaluated via (8.19.24).

For collections of integrals involving $\mathop{E_{{p}}\/}\nolimits\!\left(z\right)$ , especially for integer , see Apelblat (1983, §§7.1–7.2) and LeCaine (1945).

§8.19(xi) Further Generalizations

Keywords:: generalized exponential integral
Permalink:: http://dlmf.nist.gov/8.19.xi

For higher-order generalized exponential integrals see Meijer and Baken (1987) and Milgram (1985).

© 2010–2013 NIST / Privacy Policy / Disclaimer / Feedback; Version 1.0.6; Release date 2013-05-06 Math-Image version (See MathML) . A Printed Companionis available. 8.18 Asymptotic Expansions of $\mathop{I_{{x}}\/}\nolimits\!\left(a,b\right)$ 8.20 Asymptotic Expansions of $\mathop{E_{{p}}\/}\nolimits\!\left(z\right)$

§8.19 Generalized Exponential Integral

Contents

§8.19(i) Definition and Integral Representations

¶ Other Integral Representations

§8.19(ii) Graphics

§8.19(iii) Special Values

§8.19(iv) Series Expansions

§8.19(v) Recurrence Relation and Derivatives

¶ -Derivatives

§8.19(vi) Relation to Confluent Hypergeometric Function

§8.19(vii) Continued Fraction

§8.19(viii) Analytic Continuation

§8.19(ix) Inequalities

§8.19(x) Integrals

§8.19(xi) Further Generalizations