§3.10 Continued Fractions

Referenced by:: §1.12(vi), §14.32
Permalink:: http://dlmf.nist.gov/3.10

§3.10(i) Introduction
§3.10(ii) Relations to Power Series
§3.10(iii) Numerical Evaluation of Continued Fractions

§3.10(i) Introduction

Permalink:: http://dlmf.nist.gov/3.10.i

See §1.12 for relevant properties of continued fractions, including the following definitions:

3.10.1 $C=b_{0}+\cfrac{a_{1}}{b_{1}+\cfrac{a_{2}}{b_{2}+\cdots}},$ $a_{n}\neq 0$ ,

Symbols:: $C$ : continued fraction
Referenced by:: §3.10(ii)
Permalink:: http://dlmf.nist.gov/3.10.E1
Encodings:: TeX, pMML, png

3.10.2 $C_{n}=b_{0}+\cfrac{a_{1}}{b_{1}+\cfrac{a_{2}}{b_{2}+\cdots}}\frac{a_{n}}{b_{n}}=\frac{A_{n}}{B_{n}}.$

Symbols:: $A_{n}$ : continued fraction numerator, $B_{n}$ : continued fraction denominator and $C_{n}$ : continued fraction approximant
Referenced by:: ¶ ‣ §3.10(iii), ¶ ‣ §3.10(iii)
Permalink:: http://dlmf.nist.gov/3.10.E2
Encodings:: TeX, pMML, png

$C_{n}$ is the $n$ th approximant or convergent to $C$ .

§3.10(ii) Relations to Power Series

Notes:: See Blanch (1964). For the original source of the quotient-difference algorithm see Rutishauser (1957).
Keywords:: continued fractions
Permalink:: http://dlmf.nist.gov/3.10.ii

Every convergent, asymptotic, or formal series

3.10.3 $u_{0}+u_{1}+u_{2}+\cdots$

Symbols:: $u_{n}$ : series
Referenced by:: §3.10(ii)
Permalink:: http://dlmf.nist.gov/3.10.E3
Encodings:: TeX, pMML, png

can be converted into a continued fraction $C$ of type (3.10.1), and with the property that the $n$ th convergent $C_{n}=A_{n}/B_{n}$ to $C$ is equal to the $n$ th partial sum of the series in (3.10.3), that is,

3.10.4 $\frac{A_{n}}{B_{n}}=u_{0}+u_{1}+\dots+u_{n},$ $n=0,1,\dots$ .

Symbols:: $A_{n}$ : continued fraction numerator, $B_{n}$ : continued fraction denominator and $u_{n}$ : series
Referenced by:: §3.10(ii)
Permalink:: http://dlmf.nist.gov/3.10.E4
Encodings:: TeX, pMML, png

For instance, if none of the $u_{n}$ vanish, then we can define

3.10.5

$b_{0}=u_{0},$

$b_{1}=1,$

$a_{1}=u_{1},$

$b_{n}=1+\frac{u_{n}}{u_{{n-1}}},$

$a_{n}=-\frac{u_{n}}{u_{{n-1}}}$ , $n\geq 2$ .

Symbols:: $u_{n}$ : series
Referenced by:: §3.10(ii)
Permalink:: http://dlmf.nist.gov/3.10.E5
Encodings:: TeX, TeX, TeX, TeX, TeX, pMML, pMML, pMML, pMML, pMML, png, png, png, png, png

However, other continued fractions with the same limit may converge in a much larger domain of the complex plane than the fraction given by (3.10.4) and (3.10.5). For example, by converting the Maclaurin expansion of $\mathop{\mathrm{arctan}\/}\nolimits z$ (4.24.3), we obtain a continued fraction with the same region of convergence ( $\left|z\right|\leq 1$ , $z\neq\pm i$ ), whereas the continued fraction (4.25.4) converges for all $z\in\Complex$ except on the branch cuts from $i$ to $i\infty$ and $-i$ to $-i\infty$ .

¶ Stieltjes Fractions

Keywords:: Stieltjes fraction ( $S$ -fraction), continued fractions

A continued fraction of the form

3.10.6 $C=\cfrac{a_{0}}{1-\cfrac{a_{1}z}{1-\cfrac{a_{2}z}{1-\cdots}}}$

Symbols:: $C$ : continued fraction
Referenced by:: ¶ ‣ §3.10(ii), ¶ ‣ §3.10(ii)
Permalink:: http://dlmf.nist.gov/3.10.E6
Encodings:: TeX, pMML, png

is called a Stieltjes fraction ( $S$ -fraction). We say that it corresponds to the formal power series

3.10.7 $f(z)=c_{0}+c_{1}z+c_{2}z^{2}+\cdots$

Symbols:: $c_{n}$ : coefficients
Referenced by:: ¶ ‣ §3.10(ii), ¶ ‣ §3.10(ii), ¶ ‣ §3.10(ii)
Permalink:: http://dlmf.nist.gov/3.10.E7
Encodings:: TeX, pMML, png

if the expansion of its $n$ th convergent $C_{n}$ in ascending powers of $z$ agrees with (3.10.7) up to and including the term in $z^{{n-1}}$ , $n=1,2,3,\dots$ .

¶ Quotient-Difference Algorithm

Keywords:: continued fractions, quotient-difference algorithm, quotient-difference scheme

For several special functions the $S$ -fractions are known explicitly, but in any case the coefficients $a_{n}$ can always be calculated from the power-series coefficients by means of the quotient-difference algorithm; see Table 3.10.1.

Table 3.10.1: Quotient-difference scheme.

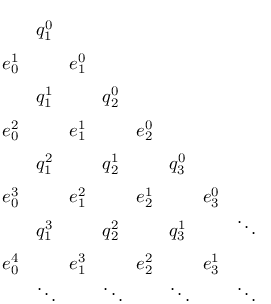$\begin{picture}(8.0,9.0)\put(0.0,7.0){$e_{0}^{1}$}\put(0.0,5.0){$e_{0}^{2}$}\put(0.0,3.0){$e_{0}^{3}$}\put(0.0,1.0){$e_{0}^{4}$}\put(1.0,8.0){$q_{1}^{0}$}\put(1.0,6.0){$q_{1}^{1}$}\put(1.0,4.0){$q_{1}^{2}$}\put(1.0,2.0){$q_{1}^{3}$}\put(1.0,0.0){$\ddots$}\put(2.0,7.0){$e_{1}^{0}$}\put(2.0,5.0){$e_{1}^{1}$}\put(2.0,3.0){$e_{1}^{2}$}\put(2.0,1.0){$e_{1}^{3}$}\put(3.0,6.0){$q_{2}^{0}$}\put(3.0,4.0){$q_{2}^{1}$}\put(3.0,2.0){$q_{2}^{2}$}\put(3.0,0.0){$\ddots$}\put(4.0,5.0){$e_{2}^{0}$}\put(4.0,3.0){$e_{2}^{1}$}\put(4.0,1.0){$e_{2}^{2}$}\put(5.0,4.0){$q_{3}^{0}$}\put(5.0,2.0){$q_{3}^{1}$}\put(5.0,0.0){$\ddots$}\put(6.0,3.0){$e_{3}^{0}$}\put(6.0,1.0){$e_{3}^{1}$}\put(7.0,2.0){$\ddots$}\put(7.0,0.0){$\ddots$}\end{picture}$

Symbols:: $e_{j}^{k}$ : element and $q_{j}^{k}$ : element
Referenced by:: ¶ ‣ §3.10(ii)
Permalink:: http://dlmf.nist.gov/3.10.T1

The first two columns in this table are defined by

3.10.8

$e_{0}^{n}=0,$ $n=1,2,\dots$ ,

$q_{1}^{n}=c_{{n+1}}/c_{n},$ $n=0,1,\dots$ ,

Symbols:: $c_{n}$ : coefficients, $e_{j}^{k}$ : element and $q_{j}^{k}$ : element
Permalink:: http://dlmf.nist.gov/3.10.E8
Encodings:: TeX, TeX, pMML, pMML, png, png

where the $c_{n}$ ( $\neq 0$ ) appear in (3.10.7). We continue by means of the rhombus rule

3.10.9

$e_{j}^{k}=e_{{j-1}}^{{k+1}}+q_{j}^{{k+1}}-q_{j}^{k},$ $j\geq 1$ , $k\geq 0$ ,

$q_{{j+1}}^{k}=q_{j}^{{k+1}}e_{j}^{{k+1}}/e_{j}^{k},$ $j\geq 1$ , $k\geq 0$ .

Symbols:: $e_{j}^{k}$ : element and $q_{j}^{k}$ : element
Permalink:: http://dlmf.nist.gov/3.10.E9
Encodings:: TeX, TeX, pMML, pMML, png, png

Then the coefficients $a_{n}$ of the $S$ -fraction (3.10.6) are given by

3.10.10

$a_{0}=c_{0},$

$a_{1}=q_{1}^{0},$

$a_{2}=e_{1}^{0},$

$a_{3}=q_{2}^{0},$

$a_{4}=e_{2}^{0},$

$\ldots.$

Symbols:: $c_{n}$ : coefficients, $e_{j}^{k}$ : element and $q_{j}^{k}$ : element
Permalink:: http://dlmf.nist.gov/3.10.E10
Encodings:: TeX, TeX, TeX, TeX, TeX, TeX, pMML, pMML, pMML, pMML, pMML, pMML, png, png, png, png, png, png

The quotient-difference algorithm is frequently unstable and may require high-precision arithmetic or exact arithmetic. A more stable version of the algorithm is discussed in Stokes (1980). For applications to Bessel functions and Whittaker functions (Chapters 10 and 13), see Gargantini and Henrici (1967).

¶ Jacobi Fractions

Keywords:: Jacobi fraction ( $J$ -fraction), continued fractions

A continued fraction of the form

3.10.11 $C=\cfrac{\beta _{0}}{1-\alpha _{0}z-\cfrac{\beta _{1}z^{2}}{1-\alpha _{1}z-\cfrac{\beta _{2}z^{2}}{1-\alpha _{2}z-\cdots}}}$

Symbols:: $C$ : continued fraction
Referenced by:: ¶ ‣ §3.10(ii)
Permalink:: http://dlmf.nist.gov/3.10.E11
Encodings:: TeX, pMML, png

is called a Jacobi fraction ( $J$ -fraction). We say that it is associated with the formal power series $f(z)$ in (3.10.7) if the expansion of its $n$ th convergent $C_{n}$ in ascending powers of $z$ , agrees with (3.10.7) up to and including the term in $z^{{2n-1}}$ , $n=1,2,3,\dots$ . For the same function $f(z)$ , the convergent $C_{n}$ of the Jacobi fraction (3.10.11) equals the convergent $C_{{2n}}$ of the Stieltjes fraction (3.10.6).

¶ Examples of $S$ - and $J$ -Fractions

For elementary functions, see §§ 4.9 and 4.35.

For special functions see §5.10 (gamma function), §7.9 (error function), §8.9 (incomplete gamma functions), §8.17(v) (incomplete beta function), §8.19(vii) (generalized exponential integral), §§10.10 and 10.33 (quotients of Bessel functions), §13.6 (quotients of confluent hypergeometric functions), §13.19 (quotients of Whittaker functions), and §15.7 (quotients of hypergeometric functions).

For further information and examples see Lorentzen and Waadeland (1992, pp. 292–330, 560–599) and Cuyt et al. (2008).

§3.10(iii) Numerical Evaluation of Continued Fractions

Notes:: See Wall (1948, pp. 17–19), Barnett et al. (1974), and Barnett (1981a).
Permalink:: http://dlmf.nist.gov/3.10.iii

¶ Forward Recurrence Algorithm

Keywords:: continued fractions

The $A_{n}$ and $B_{n}$ of (3.10.2) can be computed by means of three-term recurrence relations (1.12.5). However, this may be unstable; also overflow and underflow may occur when evaluating $A_{n}$ and $B_{n}$ (making it necessary to re-scale from time to time).

¶ Backward Recurrence Algorithm

Keywords:: continued fractions

To compute the $C_{n}$ of (3.10.2) we perform the iterated divisions

3.10.12

$u_{n}=b_{n},$

$u_{k}=b_{k}+\frac{a_{{k+1}}}{u_{{k+1}}}$ , $k=n-1,n-2,\dots,0$ .

Symbols:: $u_{n}$ : series
Permalink:: http://dlmf.nist.gov/3.10.E12
Encodings:: TeX, TeX, pMML, pMML, png, png

Then $u_{0}=C_{n}$ . To achieve a prescribed accuracy, either a priori knowledge is needed of the value of $n$ , or $n$ is determined by trial and error. In general this algorithm is more stable than the forward algorithm; see Jones and Thron (1974).

¶ Forward Series Recurrence Algorithm

Keywords:: continued fractions

The continued fraction

3.10.13 $C=\cfrac{a_{0}}{1-\cfrac{a_{1}}{1-\cfrac{a_{2}}{1-\cdots}}}$

Symbols:: $C$ : continued fraction
Referenced by:: ¶ ‣ §3.10(iii)
Permalink:: http://dlmf.nist.gov/3.10.E13
Encodings:: TeX, pMML, png

can be written in the form

3.10.14 $C=\sum _{{k=0}}^{\infty}t_{k},$

Symbols:: $C$ : continued fraction
Permalink:: http://dlmf.nist.gov/3.10.E14
Encodings:: TeX, pMML, png

where

3.10.15

$t_{0}=a_{0},$

$t_{k}=\rho _{k}t_{{k-1}},$

$\rho _{0}=0,$

$\rho _{k}=\frac{a_{k}(1+\rho _{{k-1}})}{1-a_{k}(1+\rho _{{k-1}})}$ , $k=1,2,3,\dots$ .

Permalink:: http://dlmf.nist.gov/3.10.E15
Encodings:: TeX, TeX, TeX, TeX, pMML, pMML, pMML, pMML, png, png, png, png

The $n$ th partial sum $t_{0}+t_{1}+\dots+t_{{n-1}}$ equals the $n$ th convergent of (3.10.13), $n=1,2,3,\dots$ . In contrast to the preceding algorithms in this subsection no scaling problems arise and no a priori information is needed.

In Gautschi (1979c) the forward series algorithm is used for the evaluation of a continued fraction of an incomplete gamma function (see §8.9).

¶ Steed’s Algorithm

Keywords:: Steed’s algorithm

This forward algorithm achieves efficiency and stability in the computation of the convergents $C_{n}=A_{n}/B_{n}$ , and is related to the forward series recurrence algorithm. Again, no scaling problems arise and no a priori information is needed.

Let

3.10.16

$C_{0}=b_{0},$

$D_{1}=1/b_{1},$

$\nabla C_{1}=a_{1}D_{1},$

$C_{1}=C_{0}+\nabla C_{1}.$

Symbols:: $C_{n}$ : continued fraction approximant
Permalink:: http://dlmf.nist.gov/3.10.E16
Encodings:: TeX, TeX, TeX, TeX, pMML, pMML, pMML, pMML, png, png, png, png

( $\nabla$ is the backward difference operator.) Then for $n\geq 2$ ,

3.10.17

$D_{n}=\frac{1}{D_{{n-1}}a_{n}+b_{n}},$

$\nabla C_{n}=(b_{n}D_{n}-1)\nabla C_{{n-1}},$

$C_{n}=C_{{n-1}}+\nabla C_{n}.$

Symbols:: $C_{n}$ : continued fraction approximant
Permalink:: http://dlmf.nist.gov/3.10.E17
Encodings:: TeX, TeX, TeX, pMML, pMML, pMML, png, png, png

The recurrences are continued until $(\nabla C_{n})/C_{n}$ is within a prescribed relative precision.

For further information on the preceding algorithms, including convergence in the complex plane and methods for accelerating convergence, see Blanch (1964) and Lorentzen and Waadeland (1992, Chapter 3). For the evaluation of special functions by using continued fractions see Cuyt et al. (2008), Gautschi (1967, §1), Gil et al. (2007a, Chapter 6), and Wimp (1984, Chapter 4, §5). See also §§6.18(i), 7.22(i), 8.25(iv), 10.74(v), 14.32, 28.34(ii), 29.20(i), 30.16(i), 33.23(v).