as eigenvalues of q-difference operator

SearchAdvancedHelp

(0.002 seconds)

21—30 of 155 matching pages

21: 29.7 Asymptotic Expansions

… ►

§29.7(i) Eigenvalues

… ►

29.7.1 $$a_{\nu }^m\left(k^2\right)\sim p\kappa -{\tau }_0-{\tau }_1{\kappa }^{-1}-{\tau }_2{\kappa }^{-2}-\mathrm{\cdots },$$

ⓘ

Symbols:

$a_{\nu }^n\left(k^2\right)$: eigenvalues of Lamé’s equation, $\sim$: Poincaré asymptotic expansion, $m$: nonnegative integer, $p$: nonnegative integer, $k$: real parameter, $\nu$: real parameter, $\kappa$ and ${\tau }_j$: coefficients

Permalink:

http://dlmf.nist.gov/29.7.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §29.7(i), §29.7 and Ch.29

… ►The same Poincaré expansion holds for $b_{\nu }^{m+1}\left(k^2\right)$, since ►

29.7.5 $$b_{\nu }^{m+1}\left(k^2\right)-a_{\nu }^m\left(k^2\right)=O\left({\nu }^{m+\frac{3}{2}}{\left(\frac{1-k}{1+k}\right)}^{\nu }\right),$$ $\nu \to \mathrm{\infty }$.

ⓘ

Symbols:

$O\left(x\right)$: order not exceeding, $a_{\nu }^n\left(k^2\right)$: eigenvalues of Lamé’s equation, $b_{\nu }^n\left(k^2\right)$: eigenvalues of Lamé’s equation, $m$: nonnegative integer, $k$: real parameter and $\nu$: real parameter

Referenced by:

§29.7(i)

Permalink:

http://dlmf.nist.gov/29.7.E5

Encodings:

pMML, png, TeX

See also:

Annotations for §29.7(i), §29.7 and Ch.29

…

22: 30.3 Eigenvalues

§30.3 Eigenvalues

… ►These solutions exist only for eigenvalues ${\lambda }_n^m\left({\gamma }^2\right)$, $n=m,m+1,m+2,\mathrm{\dots }$, of the parameter $\lambda$. … ►

§30.3(iii) Transcendental Equation

… ►

§30.3(iv) Power-Series Expansion

… ►Further coefficients can be found with the Maple program SWF9; see §30.18(i).

23: 28.17 Stability as $x\to \pm \mathrm{\infty }$

… ►The boundary of each region comprises the characteristic curves $a=a_n\left(q\right)$ and $a=b_n\left(q\right)$; compare Figure 28.2.1. ►

►►

Figure 28.17.1: Stability chart for eigenvalues of Mathieu’s equation (28.2.1). Magnify

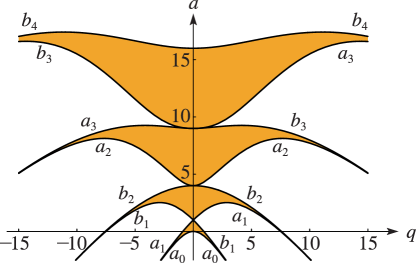24: 28.35 Tables

§28.35 Tables

… ►

Blanch and Rhodes (1955) includes ${\mathrm{𝐵𝑒}}_n(t)$, ${\mathrm{𝐵𝑜}}_n(t)$, $t=\frac{1}{2}\sqrt{q}$, $n=0(1)15$; 8D. The range of $t$ is 0 to 0.1, with step sizes ranging from 0.002 down to 0.00025. Notation: ${\mathrm{𝐵𝑒}}_n(t)=a_n\left(q\right)+2q-(4n+2)\sqrt{q}$, ${\mathrm{𝐵𝑜}}_n(t)=b_n\left(q\right)+2q-(4n-2)\sqrt{q}$.

►

Ince (1932) includes eigenvalues $a_n$, $b_n$, and Fourier coefficients for $n=0$ or $1(1)6$, $q=0(1)10(2)20(4)40$; 7D. Also ${\mathrm{ce}}_n(x,q)$, ${\mathrm{se}}_n(x,q)$ for $q=0(1)10$, $x=1(1)90$, corresponding to the eigenvalues in the tables; 5D. Notation: $a_n={\mathrm{𝑏𝑒}}_n-2q$, $b_n={\mathrm{𝑏𝑜}}_n-2q$.

… ►

National Bureau of Standards (1967) includes the eigenvalues $a_n\left(q\right)$, $b_n\left(q\right)$ for $n=0(1)3$ with $q=0(.2)20(.5)37(1)100$, and $n=4(1)15$ with $q=0(2)100$; Fourier coefficients for ${\mathrm{ce}}_n(x,q)$ and ${\mathrm{se}}_n(x,q)$ for $n=0(1)15$, $n=1(1)15$, respectively, and various values of $q$ in the interval $[0,100]$; joining factors $g_{e,n}(\sqrt{q})$, $f_{e,n}(\sqrt{q})$ for $n=0(1)15$ with $q=0(.5\text{ to }10)100$ (but in a different notation). Also, eigenvalues for large values of $q$. Precision is generally 8D.

… ►

Blanch and Clemm (1969) includes eigenvalues $a_n\left(q\right)$, $b_n\left(q\right)$ for $q=\rho {\mathrm{e}}^{\mathrm{i}\varphi }$, $\rho =0(.5)25$, $\varphi =5^{\circ }(5^{\circ }){90}^{\circ }$, $n=0(1)15$; 4D. Also $a_n\left(q\right)$ and $b_n\left(q\right)$ for $q=\mathrm{i}\rho$, $\rho =0(.5)100$, $n=0(2)14$ and $n=2(2)16$, respectively; 8D. Double points for $n=0(1)15$; 8D. Graphs are included.

…

25: 30.16 Methods of Computation

… ►

§30.16(i) Eigenvalues

… ►Approximations to eigenvalues can be improved by using the continued-fraction equations from §30.3(iii) and §30.8; see Bouwkamp (1947) and Meixner and Schäfke (1954, §3.93). … ►and real eigenvalues ${\alpha }_{1,d}$, ${\alpha }_{2,d}$, $\mathrm{\dots }$, ${\alpha }_{d,d}$, arranged in ascending order of magnitude. …The eigenvalues of $𝐀$ can be computed by methods indicated in §§3.2(vi), 3.2(vii). … ►which yields ${\lambda }_4^2\left(10\right)=\mathrm{13.97907\hspace{0.33em}345}$. …

26: 12.16 Mathematical Applications

… ►Sleeman (1968b) considers certain orthogonality properties of the PCFs and corresponding eigenvalues. In Brazel et al. (1992) exponential asymptotics are considered in connection with an eigenvalue problem involving PCFs. …

27: 30.18 Software

… ►

SWF1: ${\lambda }_n^m\left({\gamma }^2\right)$.

… ►

§30.18(ii) Eigenvalues ${\lambda }_n^m\left({\gamma }^2\right)$

…

28: 30.17 Tables

§30.17 Tables

►

Stratton et al. (1956) tabulates quantities closely related to ${\lambda }_n^m\left({\gamma }^2\right)$ and $a_{n,k}^m({\gamma }^2)$ for $0\le m\le 8$, $m\le n\le 8$, $-64\le {\gamma }^2\le 64$. Precision is 7S.

►

Flammer (1957) includes 18 tables of eigenvalues, expansion coefficients, spheroidal wave functions, and other related quantities. Precision varies between 4S and 10S.

… ►

Van Buren et al. (1975) gives ${\lambda }_n^0\left({\gamma }^2\right)$, ${\mathrm{𝖯𝗌}}_n^0(x,{\gamma }^2)$ for $0\le n\le 49$, $-1600\le {\gamma }^2\le 1600$, $-1\le x\le 1$. Precision is 8S.

►

Zhang and Jin (1996) includes 24 tables of eigenvalues, spheroidal wave functions and their derivatives. Precision varies between 6S and 8S.

…

29: Bibliography R

… ►

Methods of Modern Mathematical Physics, Vol. 4, Analysis of Operators. Academic Press, New York.

ⓘ

External Links:

ISBN 0-12-585004-2(vol.4), MathReview (P. R. Chernoff)

Referenced by:

§1.18(x).

Encodings:

BibTeX

… ►

On the computation of Lamé functions, of eigenvalues and eigenfunctions of some potential operators. Z. Angew. Math. Mech. 78 (1), pp. 66–72.

ⓘ

External Links:

ISSN 0044-2267, Document, MathReview Entry, ZentralBlatt

Referenced by:

§29.20(ii).

Encodings:

BibTeX

… ►

On the foundations of combinatorial theory. VIII. Finite operator calculus. J. Math. Anal. Appl. 42, pp. 684–760.

ⓘ

External Links:

ISSN 0022-247X, Document, Link, MathReview (P. Saphar), ZentralBlatt

Referenced by:

§18.2(xii).

Encodings:

BibTeX

… ►

On Simple Waves with Profiles in the form of some Special Functions—Chebyshev-Hermite, Mathieu, Whittaker—in Two-phase Media. In Differential Operators and Related Topics, Vol. I (Odessa, 1997), Operator Theory: Advances and Applications, Vol. 117, pp. 313–322.

ⓘ

External Links:

ISBN 3-7643-6287-1, MathReview Entry, ZentralBlatt

Referenced by:

5th item.

Encodings:

BibTeX

…

30: 3.2 Linear Algebra

… ►

§3.2(iv) Eigenvalues and Eigenvectors

… ► ►

§3.2(v) Condition of Eigenvalues

… ►has the same eigenvalues as $𝐀$. … ►

§3.2(vii) Computation of Eigenvalues

…