28 Mathieu Functions and Hill’s Equation Mathieu Functions of Noninteger Order 28.16 Asymptotic Expansions for Large

§28.17 Stability as $x\to\pm\infty$

Notes:: See Arscott (1964b, §6.2) and Meixner and Schäfke (1954, §§2.31–2.32). Figure 28.17.1 was recomputed by the author.
Keywords:: Mathieu’s equation
Referenced by:: §28.33(iii)
Permalink:: http://dlmf.nist.gov/28.17

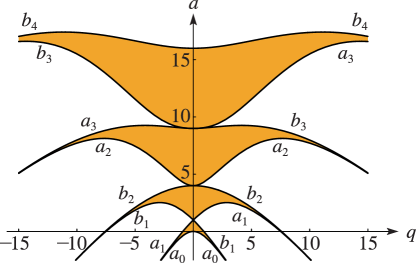
If all solutions of (28.2.1) are bounded when $x\to\pm\infty$ along the real axis, then the corresponding pair of parameters is called stable. All other pairs are unstable.

For example, positive real values of with comprise stable pairs, as do values of and that correspond to real, but noninteger, values of $\nu$ .

However, if $\imagpart{\nu}\neq 0$ , then always comprises an unstable pair. For example, as $x\to+\infty$ one of the solutions $\mathop{\mathrm{me}_{{\nu}}\/}\nolimits\!\left(x,q\right)$ and $\mathop{\mathrm{me}_{{\nu}}\/}\nolimits\!\left(-x,q\right)$ tends to 0 and the other is unbounded (compare Figure 28.13.5). Also, all nontrivial solutions of (28.2.1) are unbounded on $\Real$ .

For real and $(\neq 0)$ the stable regions are the open regions indicated in color in Figure 28.17.1. The boundary of each region comprises the characteristic curves $a=\mathop{a_{{n}}\/}\nolimits\!\left(q\right)$ and $a=\mathop{b_{{n}}\/}\nolimits\!\left(q\right)$ ; compare Figure 28.2.1.

Figure 28.17.1: Stability chart for eigenvalues of Mathieu’s equation (28.2.1).

Referenced by:: §28.17, §28.17, §28.33(iii)
Permalink:: http://dlmf.nist.gov/28.17.F1
Encodings:: pdf, png

© 2010–2013 NIST / Privacy Policy / Disclaimer / Feedback; Version 1.0.6; Release date 2013-05-06 Math-Image version (See MathML) . A Printed Companionis available. 28.16 Asymptotic Expansions for Large

28.18 Integrals and Integral Equations