Schur parameters

SearchAdvancedHelp

(0.003 seconds)

1—10 of 386 matching pages

1: 18.33 Polynomials Orthogonal on the Unit Circle

… ►

18.33.22 $$p^{\ast }(z)\equiv z^n\overline{p({\overline{z}}^{-1})}=\sum _{k=0}^n\overline{c_{n-k}}{z}^k.$$

ⓘ

Symbols:

$\overline{z}$: complex conjugate, $\equiv$: equals by definition, $z$: complex variable, $k$: nonnegative integer and $n$: nonnegative integer

Source:

Simon (2005a, (1.1.7))

Permalink:

http://dlmf.nist.gov/18.33.E22

Encodings:

pMML, png, TeX

See also:

Annotations for §18.33(vi), §18.33(vi), §18.33 and Ch.18

►The Verblunsky coefficients (also called Schur parameters or reflection coefficients) are the coefficients ${\alpha }_n$ in the Szegő recurrence relations …

2: Bibliography D

… ►

Accurate and efficient evaluation of Schur and Jack functions. Math. Comp. 75 (253), pp. 223–239.

ⓘ

Notes:

For Fortran software for these functions, see Plamen Koev’s home page.

External Links:

Home Page, ISSN 0025-5718, Document, MathReview Entry, ZentralBlatt

Referenced by:

1st item.

Encodings:

BibTeX

… ►

Uniform asymptotic expansions for prolate spheroidal functions with large parameters. SIAM J. Math. Anal. 17 (6), pp. 1495–1524.

ⓘ

External Links:

ISSN 0036-1410, Document, MathReview (R. K. Gupta), ZentralBlatt

Referenced by:

§30.9(i).

Encodings:

BibTeX

… ►

Conical functions with one or both parameters large. Proc. Roy. Soc. Edinburgh Sect. A 119 (3-4), pp. 311–327.

ⓘ

External Links:

ISSN 0308-2105, MathReview (F. W. J. Olver), ZentralBlatt

Referenced by:

§14.20(i), §14.20(ix), §14.20(ix), §14.20(viii), §14.23.

Encodings:

BibTeX

►

Uniform asymptotic expansions for oblate spheroidal functions I: Positive separation parameter $\lambda$ . Proc. Roy. Soc. Edinburgh Sect. A 121 (3-4), pp. 303–320.

ⓘ

External Links:

ISSN 0308-2105, MathReview (Archibald D. MacGillivray), ZentralBlatt

Referenced by:

§30.9(ii).

Encodings:

BibTeX

… ►

Uniform asymptotic expansions for oblate spheroidal functions II: Negative separation parameter $\lambda$ . Proc. Roy. Soc. Edinburgh Sect. A 125 (4), pp. 719–737.

ⓘ

External Links:

ISSN 0308-2105, MathReview (Archibald D. MacGillivray), ZentralBlatt

Referenced by:

§30.9(ii).

Encodings:

BibTeX

…

3: Bibliography M

… ►

On one-parameter families of Painlevé III. Stud. Appl. Math. 101 (3), pp. 321–341.

ⓘ

External Links:

ISSN 0022-2526, Document, MathReview (Andrei A. Kapaev), ZentralBlatt

Referenced by:

§32.10(iii).

Encodings:

BibTeX

… ►

Fast computation of the Gauss hypergeometric function with all its parameters complex with application to the Pöschl-Teller-Ginocchio potential wave functions. Comput. Phys. Comm. 178 (7), pp. 535–551.

ⓘ

External Links:

ISSN 0010-4655, Document, FullText, MathReview Entry, ZentralBlatt

Referenced by:

§15.19(i), §15.19(i).

Encodings:

BibTeX

… ►

Infinite families of exact sums of squares formulas, Jacobi elliptic functions, continued fractions, and Schur functions. Ramanujan J. 6 (1), pp. 7–149.

ⓘ

External Links:

Document, ZentralBlatt

Referenced by:

§27.13(iv).

Encodings:

BibTeX

… ►

The characteristic numbers of the Mathieu equation with purely imaginary parameter. Phil. Mag. Series 7 8 (53), pp. 834–840.

ⓘ

External Links:

Document, ZentralBlatt

Referenced by:

§28.7.

Encodings:

BibTeX

… ►

Tables of the functions of the parabolic cylinder for negative integer parameters. Zastos. Mat. 13, pp. 261–273.

ⓘ

External Links:

MathReview, ZentralBlatt

Referenced by:

7th item.

Encodings:

BibTeX

…

4: 31.13 Asymptotic Approximations

§31.13 Asymptotic Approximations

►For asymptotic approximations for the accessory parameter eigenvalues $q_m$, see Fedoryuk (1991) and Slavyanov (1996). …

5: 31.3 Basic Solutions

… ►

31.3.2 $$a\gamma c_1-q{c}_0=0,$$

ⓘ

Symbols:

$\gamma$: real or complex parameter, $a$: complex parameter, $q$: real or complex parameter and $c_j$: coefficients

Permalink:

http://dlmf.nist.gov/31.3.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §31.3(i), §31.3 and Ch.31

… ►

31.3.5 $$z^{1-\gamma }H\mathrm{\ell }(a,(a\delta +ϵ)(1-\gamma )+q;\alpha +1-\gamma ,\beta +1-\gamma ,2-\gamma ,\delta ;z).$$

ⓘ

Symbols:

$H\mathrm{\ell }(a,q;\alpha ,\beta ,\gamma ,\delta ;z)$: Heun functions, $z$: complex variable, $\gamma$: real or complex parameter, $\delta$: real or complex parameter, $ϵ$: real or complex parameter, $a$: complex parameter, $q$: real or complex parameter, $\alpha$: real or complex parameter and $\beta$: real or complex parameter

Referenced by:

§31.3(iii), §31.7(ii)

Permalink:

http://dlmf.nist.gov/31.3.E5

Encodings:

pMML, png, TeX

See also:

Annotations for §31.3(i), §31.3 and Ch.31

… ►

31.3.6 $$H\mathrm{\ell }(1-a,\alpha \beta -q;\alpha ,\beta ,\delta ,\gamma ;1-z),$$

ⓘ

Symbols:

$H\mathrm{\ell }(a,q;\alpha ,\beta ,\gamma ,\delta ;z)$: Heun functions, $z$: complex variable, $\gamma$: real or complex parameter, $\delta$: real or complex parameter, $a$: complex parameter, $q$: real or complex parameter, $\alpha$: real or complex parameter and $\beta$: real or complex parameter

Permalink:

http://dlmf.nist.gov/31.3.E6

Encodings:

pMML, png, TeX

See also:

Annotations for §31.3(ii), §31.3 and Ch.31

►

31.3.7 $${(1-z)}^{1-\delta }H\mathrm{\ell }(1-a,((1-a)\gamma +ϵ)(1-\delta )+\alpha \beta -q;\alpha +1-\delta ,\beta +1-\delta ,2-\delta ,\gamma ;1-z).$$

ⓘ

Symbols:

$H\mathrm{\ell }(a,q;\alpha ,\beta ,\gamma ,\delta ;z)$: Heun functions, $z$: complex variable, $\gamma$: real or complex parameter, $\delta$: real or complex parameter, $ϵ$: real or complex parameter, $a$: complex parameter, $q$: real or complex parameter, $\alpha$: real or complex parameter and $\beta$: real or complex parameter

Permalink:

http://dlmf.nist.gov/31.3.E7

Encodings:

pMML, png, TeX

See also:

Annotations for §31.3(ii), §31.3 and Ch.31

… ►

31.3.8 $$H\mathrm{\ell }(\frac{a}{a-1},\frac{\alpha \beta a-q}{a-1};\alpha ,\beta ,ϵ,\delta ;\frac{a-z}{a-1}),$$

ⓘ

Symbols:

$H\mathrm{\ell }(a,q;\alpha ,\beta ,\gamma ,\delta ;z)$: Heun functions, $z$: complex variable, $\delta$: real or complex parameter, $ϵ$: real or complex parameter, $a$: complex parameter, $q$: real or complex parameter, $\alpha$: real or complex parameter and $\beta$: real or complex parameter

Permalink:

http://dlmf.nist.gov/31.3.E8

Encodings:

pMML, png, TeX

See also:

Annotations for §31.3(ii), §31.3 and Ch.31

…

6: 29.11 Lamé Wave Equation

… ►

29.11.1 $$\frac{d^{2}w}{{dz}^2}+(h-\nu (\nu +1)k^2{\mathrm{sn}}^2(z,k)+k^2{\omega }^2{\mathrm{sn}}^4(z,k))w=0,$$

ⓘ

Symbols:

$\mathrm{sn}(z,k)$: Jacobian elliptic function, $\frac{df}{dx}$: derivative of $f$ with respect to $x$ , $z$: complex variable, $h$: real parameter, $k$: real parameter, $\nu$: real parameter, $\omega$: parameter and $w(z)$: solution

Referenced by:

§29.11, §29.11, §29.18(ii), §29.7(ii)

Permalink:

http://dlmf.nist.gov/29.11.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §29.11 and Ch.29

►in which $\omega$ is another parameter. … ►For properties of the solutions of (29.11.1) see Arscott (1956, 1959), Arscott (1964b, Chapter X), Erdélyi et al. (1955, §16.14), Fedoryuk (1989), and Müller (1966a, b, c).

7: 31.14 General Fuchsian Equation

… ►

31.14.1 $$\frac{d^{2}w}{{dz}^2}+\left(\sum _{j=1}^N\frac{{\gamma }_j}{z-a_j}\right)\frac{dw}{dz}+\left(\sum _{j=1}^N\frac{q_j}{z-a_j}\right)w=0,$$ ${\sum }_{j=1}^N{q}_j=0$.

ⓘ

Symbols:

$\frac{df}{dx}$: derivative of $f$ with respect to $x$ , $z$: complex variable, $\gamma$: real or complex parameter, $j$: nonnegative integer, $a$: complex parameter, $q$: real or complex parameter and $N+1$: number of singularities

Referenced by:

§31.15(i)

Permalink:

http://dlmf.nist.gov/31.14.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §31.14(i), §31.14 and Ch.31

… ►

$\alpha \beta ={\displaystyle \sum _{j=1}^N}{a}_j{q}_j.$

►The three sets of parameters comprise the singularity parameters $a_j$, the exponent parameters $\alpha ,\beta ,{\gamma }_j$, and the $N-2$ free accessory parameters $q_j$. With $a_1=0$ and $a_2=1$ the total number of free parameters is $3N-3$. … ►

31.14.3 $$w(z)=\left(\prod _{j=1}^N{(z-a_j)}^{-{\gamma }_j/2}\right)W(z),$$

ⓘ

Symbols:

$z$: complex variable, $\gamma$: real or complex parameter, $j$: nonnegative integer, $a$: complex parameter, $N+1$: number of singularities and $W(z)$: solution

Permalink:

http://dlmf.nist.gov/31.14.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §31.14(i), §31.14(i), §31.14 and Ch.31

…

8: 28.17 Stability as $x\to \pm \mathrm{\infty }$

§28.17 Stability as $x\to \pm \mathrm{\infty }$

►If all solutions of (28.2.1) are bounded when $x\to \pm \mathrm{\infty }$ along the real axis, then the corresponding pair of parameters $(a,q)$ is called stable. … ►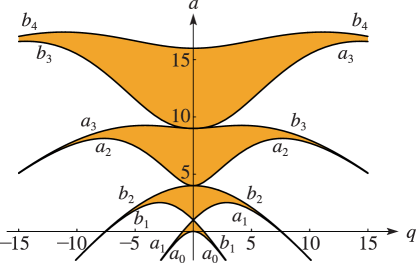

►►

Figure 28.17.1: Stability chart for eigenvalues of Mathieu’s equation (28.2.1). Magnify

9: 31.1 Special Notation

… ► ►►►►

$x$, $y$	real variables.
…
$a$	complex parameter, $|a|\ge 1,a\ne 1$.
$q,\alpha ,\beta ,\gamma ,\delta ,ϵ,\nu$	complex parameters.

… ►Sometimes the parameters are suppressed.

10: 34.8 Approximations for Large Parameters

§34.8 Approximations for Large Parameters

►For large values of the parameters in the $\mathit{3}j$, $\mathit{6}j$, and $\mathit{9}j$ symbols, different asymptotic forms are obtained depending on which parameters are large. … ►and the symbol $o\left(1\right)$ denotes a quantity that tends to zero as the parameters tend to infinity, as in §2.1(i). …