§10.23 Sums
Contents
- §10.23(i) Multiplication Theorem
- §10.23(ii) Addition Theorems
- §10.23(iii) Series Expansions of Arbitrary Functions
- §10.23(iv) Compendia
§10.23(i) Multiplication Theorem
| 10.23.1 | |||
| . | |||
If and the upper signs are taken, then the restriction on is unnecessary.
§10.23(ii) Addition Theorems
Neumann’s Addition Theorem
| 10.23.2 | |||
| . | |||
The restriction is unnecessary when and is an integer. Special cases are:
| 10.23.3 | |||
| 10.23.4 | |||
| , | |||
| 10.23.5 | |||
Graf’s and Gegenbauer’s Addition Theorems
Define
| 10.23.6 | ||||
the branches being continuous and chosen so that and as . If , are real and positive and , then and are real and nonnegative, and the geometrical relationship is shown in Figure 10.23.1.
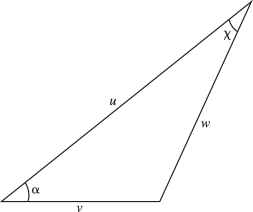
| 10.23.7 | |||
| . | |||
| 10.23.8 | |||
| , , | |||
where is Gegenbauer’s polynomial (§18.3). The restriction is unnecessary in (10.23.7) when and is an integer, and in (10.23.8) when .
The degenerate form of (10.23.8) when is given by
| 10.23.9 | |||
| . | |||
See also §10.12.
Partial Fractions
For expansions of products of Bessel functions of the first kind in partial fractions see Rogers (2005).
§10.23(iii) Series Expansions of Arbitrary Functions
Neumann’s Expansion
| 10.23.10 | |||
| , | |||
where is the distance of the nearest singularity of the analytic function from ,
| 10.23.11 | |||
| , | |||
and is Neumann’s polynomial, defined by the generating function:
| 10.23.12 | |||
| . | |||
is a polynomial of degree in and
| 10.23.13 | |||
| . | |||
Examples
Fourier–Bessel Expansion
Assume satisfies
| 10.23.18 | |||
and define
| 10.23.19 | |||
| , | |||
where is as in §10.21(i). If , then
| 10.23.20 | |||
provided that is of bounded variation (§1.4(v)) on an interval with . This result is proved in Watson (1944, Chapter 18) and further information is provided in this reference, including the behavior of the series near and .
As an example,
| 10.23.21 | |||
| . | |||
(Note that when the left-hand side is 1 and the right-hand side is 0.)
