Fourier%E2%80%93Bessel%20expansion

SearchAdvancedHelp

(0.002 seconds)

11—20 of 460 matching pages

11: Bibliography O

… ►

Tables of Fourier Transforms and Fourier Transforms of Distributions. Springer-Verlag, Berlin.

ⓘ

External Links:

ISBN 3-540-50630-6; 0-387-50630-6, MathReview, ZentralBlatt

Referenced by:

§1.14(viii), §10.22(vi), §10.43(vi), §11.10(x), §11.7(v), §11.9(iv), §12.12, §13.10(iv), §13.23(ii), §18.17(ix), §6.14(iii), §7.14(iii).

Encodings:

BibTeX

… ►

Fourier Expansions. A Collection of Formulas. Academic Press, New York-London.

ⓘ

External Links:

MathReview, ZentralBlatt

Referenced by:

§1.8(v), §22.11, §4.27.

Encodings:

BibTeX

… ►

Asymptotic expansions for $q$-gamma, $q$-exponential, and $q$-Bessel functions. J. Math. Anal. Appl. 186 (3), pp. 896–913.

ⓘ

External Links:

ISSN 0022-247X, Document, MathReview (P. K. Banerji), ZentralBlatt

Referenced by:

§5.18(ii).

Encodings:

BibTeX

… ►

An error analysis of the modified Clenshaw method for evaluating Chebyshev and Fourier series. J. Inst. Math. Appl. 20 (3), pp. 379–391.

ⓘ

External Links:

Document, MathReview (David L. Elliott), ZentralBlatt

Referenced by:

§3.11(ii).

Encodings:

BibTeX

… ►

Numerical evaluation of the dilogarithm of complex argument. Celestial Mech. Dynam. Astronom. 62 (1), pp. 93–98.

ⓘ

External Links:

ISSN 0923-2958, Document, MathReview (Bruce C. Berndt), ZentralBlatt

Referenced by:

§25.18(i).

Encodings:

BibTeX

…

12: Bibliography K

… ►

A proof of the $q$-Macdonald-Morris conjecture for $B{C}_n$ . Mem. Amer. Math. Soc. 108 (516), pp. vi+80.

ⓘ

External Links:

ISSN 0065-9266, MathReview (Eric M. Opdam), ZentralBlatt

Referenced by:

§17.14.

Encodings:

BibTeX

… ►

The computation of the sums of negative even powers of roots of Bessel functions. Doklady Akad. Nauk SSSR (N.S.) 77, pp. 561–564.

ⓘ

External Links:

MathReview (A. Erdélyi), ZentralBlatt

Referenced by:

§10.21(xiii).

Encodings:

BibTeX

… ►

Linear convergence and the bisection algorithm. Amer. Math. Monthly 93 (1), pp. 48–51.

ⓘ

External Links:

ISSN 0002-9890, FullText, MathReview (J. G. Herriot), ZentralBlatt

Referenced by:

§3.8(iii).

Encodings:

BibTeX

… ►

Fourier Analysis. 2nd edition, Cambridge University Press, Cambridge.

ⓘ

External Links:

ISBN 0-521-38991-7, MathReview, ZentralBlatt

Referenced by:

§1.15(iii), §20.13.

Encodings:

BibTeX

… ►

A Handbook of Methods of Approximate Fourier Transformation and Inversion of the Laplace Transformation. Mir, Moscow.

ⓘ

Notes:

Translated from the Russian by George Yankovsky. Reprint of the 1977 translation

External Links:

MathReview, ZentralBlatt

Referenced by:

§3.5(viii).

Encodings:

BibTeX

…

13: Peter L. Walker

… ►Walker’s books are An Introduction to Complex Analysis, published by Hilger in 1974, The Theory of Fourier Series and Integrals, published by Wiley in 1986, Elliptic Functions. A Constructive Approach, published by Wiley in 1996, and Examples and Theorems in Analysis, published by Springer in 2004. … ►

20 Theta Functions

…

14: 28.11 Expansions in Series of Mathieu Functions

§28.11 Expansions in Series of Mathieu Functions

… ►See Meixner and Schäfke (1954, §2.28), and for expansions in the case of the exceptional values of $q$ see Meixner et al. (1980, p. 33). … ►

28.11.3 $$1=2\sum _{n=0}^{\mathrm{\infty }}{A}_0^{2n}(q){\mathrm{ce}}_{2n}(z,q),$$

ⓘ

Symbols:

${\mathrm{ce}}_n(z,q)$: Mathieu function, $q=h^2$: parameter, $n$: integer, $z$: complex variable and $A_m(q)$: Fourier coefficient

Permalink:

http://dlmf.nist.gov/28.11.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §28.11, §28.11 and Ch.28

►

28.11.4 $$\cos 2mz=\sum _{n=0}^{\mathrm{\infty }}{A}_{2m}^{2n}(q){\mathrm{ce}}_{2n}(z,q),$$ $m\ne 0$,

ⓘ

Symbols:

${\mathrm{ce}}_n(z,q)$: Mathieu function, $\cos z$: cosine function, $m$: integer, $q=h^2$: parameter, $n$: integer, $z$: complex variable and $A_m(q)$: Fourier coefficient

Permalink:

http://dlmf.nist.gov/28.11.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §28.11, §28.11 and Ch.28

… ►

28.11.7 $$\sin (2m+2)z=\sum _{n=0}^{\mathrm{\infty }}{B}_{2m+2}^{2n+2}(q){\mathrm{se}}_{2n+2}(z,q).$$

ⓘ

Symbols:

${\mathrm{se}}_n(z,q)$: Mathieu function, $\sin z$: sine function, $m$: integer, $q=h^2$: parameter, $n$: integer, $z$: complex variable and $B_m(q)$: Fourier coefficient

Permalink:

http://dlmf.nist.gov/28.11.E7

Encodings:

pMML, png, TeX

See also:

Annotations for §28.11, §28.11 and Ch.28

15: 6.16 Mathematical Applications

… ►Consider the Fourier series … ►Compare Figure 6.16.1. … ►It occurs with Fourier-series expansions of all piecewise continuous functions. … … ►

►►

Figure 6.16.2: The logarithmic integral $\mathrm{li}\left(x\right)$, together with vertical bars indicating the value of $\pi (x)$ for $x=10,20,\mathrm{\dots },1000$. Magnify

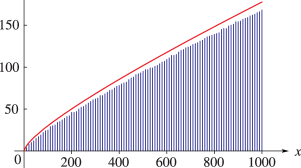16: 28.35 Tables

§28.35 Tables

… ►

Ince (1932) includes eigenvalues $a_n$, $b_n$, and Fourier coefficients for $n=0$ or $1(1)6$, $q=0(1)10(2)20(4)40$; 7D. Also ${\mathrm{ce}}_n(x,q)$, ${\mathrm{se}}_n(x,q)$ for $q=0(1)10$, $x=1(1)90$, corresponding to the eigenvalues in the tables; 5D. Notation: $a_n={\mathrm{𝑏𝑒}}_n-2q$, $b_n={\mathrm{𝑏𝑜}}_n-2q$.

… ►

National Bureau of Standards (1967) includes the eigenvalues $a_n\left(q\right)$, $b_n\left(q\right)$ for $n=0(1)3$ with $q=0(.2)20(.5)37(1)100$, and $n=4(1)15$ with $q=0(2)100$; Fourier coefficients for ${\mathrm{ce}}_n(x,q)$ and ${\mathrm{se}}_n(x,q)$ for $n=0(1)15$, $n=1(1)15$, respectively, and various values of $q$ in the interval $[0,100]$; joining factors $g_{e,n}(\sqrt{q})$, $f_{e,n}(\sqrt{q})$ for $n=0(1)15$ with $q=0(.5\text{ to }10)100$ (but in a different notation). Also, eigenvalues for large values of $q$. Precision is generally 8D.

►

Stratton et al. (1941) includes $b_n$, $b_n^{\prime }$, and the corresponding Fourier coefficients for ${\mathrm{Se}}_n(c,x)$ and ${\mathrm{So}}_n(c,x)$ for $n=0$ or $1(1)4$, $c=0(.1\text{or}.2)4.5$. Precision is mostly 5S. Notation: $c=2\sqrt{q}$, $b_n=a_n+2q$, $b_n^{\prime }=b_n+2q$, and for ${\mathrm{Se}}_n(c,x)$, ${\mathrm{So}}_n(c,x)$ see §28.1.

►

Zhang and Jin (1996, pp. 521–532) includes the eigenvalues $a_n\left(q\right)$, $b_{n+1}\left(q\right)$ for $n=0(1)4$, $q=0(1)50$; $n=0(1)20$ ($a$’s) or 19 ($b$’s), $q=1,3,5,10,15,25,50(50)200$. Fourier coefficients for ${\mathrm{ce}}_n(x,10)$, ${\mathrm{se}}_{n+1}(x,10)$, $n=0(1)7$. Mathieu functions ${\mathrm{ce}}_n(x,10)$, ${\mathrm{se}}_{n+1}(x,10)$, and their first $x$-derivatives for $n=0(1)4$, $x=0(5^{\circ }){90}^{\circ }$. Modified Mathieu functions ${\mathrm{Mc}}_n^{(j)}(x,\sqrt{10})$, ${\mathrm{Ms}}_{n+1}^{(j)}(x,\sqrt{10})$, and their first $x$-derivatives for $n=0(1)4$, $j=1,2$, $x=0(.2)4$. Precision is mostly 9S.

…

17: 28.24 Expansions in Series of Cross-Products of Bessel Functions or Modified Bessel Functions

§28.24 Expansions in Series of Cross-Products of Bessel Functions or Modified Bessel Functions

… ►Also, with $I_n$ and $K_n$ denoting the modified Bessel functions (§10.25(ii)), and again with $s=0,1,2,\mathrm{\dots }$, … ►

28.24.10 $${\epsilon }_s{\mathrm{Ke}}_{2m}(z,h)=\sum _{\mathrm{\ell }=0}^{\mathrm{\infty }}\frac{A_{2\mathrm{\ell }}^{2m}(h^2)}{A_{2s}^{2m}(h^2)}\left(I_{\mathrm{\ell }-s}\left(h{\mathrm{e}}^{-z}\right)K_{\mathrm{\ell }+s}\left(h{\mathrm{e}}^z\right)+I_{\mathrm{\ell }+s}\left(h{\mathrm{e}}^{-z}\right)K_{\mathrm{\ell }-s}\left(h{\mathrm{e}}^z\right)\right),$$

ⓘ

Symbols:

$\mathrm{e}$: base of natural logarithm, $I_{\nu }\left(z\right)$: modified Bessel function of the first kind, $K_{\nu }\left(z\right)$: modified Bessel function of the second kind, ${\mathrm{Ke}}_n(z,h)$: modified Mathieu function, $m$: integer, $h$: parameter, $z$: complex variable, ${\epsilon }_s$: constants and $A_m(q)$: Fourier coefficient

A&S Ref:

20.8.9

Permalink:

http://dlmf.nist.gov/28.24.E10

Encodings:

pMML, png, TeX

See also:

Annotations for §28.24 and Ch.28

… ►The expansions (28.24.1)–(28.24.13) converge absolutely and uniformly on compact sets of the $z$-plane. ►For further power series of Mathieu radial functions of integer order for small parameters and improved convergence rate see Larsen et al. (2009).

18: Bibliography T

… ►

LSFBTR: A subroutine for calculating spherical Bessel transforms. Comput. Phys. Comm. 30 (1), pp. 93–99.

ⓘ

Notes:

Single-precision Fortran.

External Links:

ISSN 0010-4655, Document, Code

Referenced by:

9th item.

Encodings:

BibTeX

… ►

Some definite integrals and Fourier series for Jacobian elliptic functions. Z. Angew. Math. Mech. 49, pp. 95–96.

ⓘ

External Links:

ISSN 0044-2267, Document, MathReview (B. C. Carlson), ZentralBlatt

Referenced by:

§22.11.

Encodings:

BibTeX

… ►

Fourier Analysis on Finite Groups and Applications. London Mathematical Society Student Texts, Vol. 43, Cambridge University Press, Cambridge.

ⓘ

External Links:

ISBN 0-521-45718-1, MathReview (Stefan Kühnlein), ZentralBlatt

Referenced by:

§5.16.

Encodings:

BibTeX

… ►

Introduction to the Theory of Fourier Integrals. Third edition, Chelsea Publishing Co., New York.

ⓘ

Notes:

Original edition was published in 1937 by Oxford University Press. Expanded bibliography and some improvements were made for the second and third editions.

External Links:

ISBN 0-8284-0324-4, MathReview, ZentralBlatt

Referenced by:

§1.14(i), §1.14(ii), §1.14(iv), §1.14(v), §1.14(vii), §1.8(iv), §10.22(v), §10.32(iii), §5.13.

Encodings:

BibTeX

… ►

Fourier Series. Prentice-Hall Inc., Englewood Cliffs, N.J..

ⓘ

Notes:

Translated from the Russian by Richard A. Silverman. Second English edition published by Dover Publications Inc., New York, 1976.

External Links:

MathReview (R. P. Boas, Jr.), ZentralBlatt

Referenced by:

§1.8(i), §1.8(ii).

Encodings:

BibTeX

…

19: 27.10 Periodic Number-Theoretic Functions

… ►Every function periodic (mod $k$) can be expressed as a finite Fourier series of the form … ►is a periodic function of $n(modk)$ and has the finite Fourier-series expansion … ►The finite Fourier expansion of a primitive Dirichlet character $\chi (modk)$ has the form …

20: 28.23 Expansions in Series of Bessel Functions

§28.23 Expansions in Series of Bessel Functions

… ►

28.23.6 $${\mathrm{Mc}}_{2m}^{(j)}(z,h)={(-1)}^m{\left({\mathrm{ce}}_{2m}(0,h^2)\right)}^{-1}\sum _{\mathrm{\ell }=0}^{\mathrm{\infty }}{(-1)}^{\mathrm{\ell }}{A}_{2\mathrm{\ell }}^{2m}(h^2){𝒞}_{2\mathrm{\ell }}^{(j)}(2h\cosh z),$$

ⓘ

Symbols:

${\mathrm{ce}}_n(z,q)$: Mathieu function, $\cosh z$: hyperbolic cosine function, ${\mathrm{Mc}}_n^{(j)}(z,h)$: radial Mathieu function, $m$: integer, $h$: parameter, $j$: integer, $z$: complex variable, ${𝒞}_{\mu }^{(j)}$: cylinder functions and $A_m(q)$: Fourier coefficient

A&S Ref:

20.6.12

Referenced by:

§28.23

Permalink:

http://dlmf.nist.gov/28.23.E6

Encodings:

pMML, png, TeX

See also:

Annotations for §28.23 and Ch.28

►

28.23.7 $${\mathrm{Mc}}_{2m}^{(j)}(z,h)={(-1)}^m{\left({\mathrm{ce}}_{2m}(\frac{1}{2}\pi ,h^2)\right)}^{-1}\sum _{\mathrm{\ell }=0}^{\mathrm{\infty }}{A}_{2\mathrm{\ell }}^{2m}(h^2){𝒞}_{2\mathrm{\ell }}^{(j)}(2h\sinh z),$$

ⓘ

Symbols:

${\mathrm{ce}}_n(z,q)$: Mathieu function, $\pi$: the ratio of the circumference of a circle to its diameter, $\sinh z$: hyperbolic sine function, ${\mathrm{Mc}}_n^{(j)}(z,h)$: radial Mathieu function, $m$: integer, $h$: parameter, $j$: integer, $z$: complex variable, ${𝒞}_{\mu }^{(j)}$: cylinder functions and $A_m(q)$: Fourier coefficient

Permalink:

http://dlmf.nist.gov/28.23.E7

Encodings:

pMML, png, TeX

See also:

Annotations for §28.23 and Ch.28

►

28.23.8 $${\mathrm{Mc}}_{2m+1}^{(j)}(z,h)={(-1)}^m{\left({\mathrm{ce}}_{2m+1}(0,h^2)\right)}^{-1}\sum _{\mathrm{\ell }=0}^{\mathrm{\infty }}{(-1)}^{\mathrm{\ell }}{A}_{2\mathrm{\ell }+1}^{2m+1}(h^2){𝒞}_{2\mathrm{\ell }+1}^{(j)}(2h\cosh z),$$

ⓘ

Symbols:

${\mathrm{ce}}_n(z,q)$: Mathieu function, $\cosh z$: hyperbolic cosine function, ${\mathrm{Mc}}_n^{(j)}(z,h)$: radial Mathieu function, $m$: integer, $h$: parameter, $j$: integer, $z$: complex variable, ${𝒞}_{\mu }^{(j)}$: cylinder functions and $A_m(q)$: Fourier coefficient

Permalink:

http://dlmf.nist.gov/28.23.E8

Encodings:

pMML, png, TeX

See also:

Annotations for §28.23 and Ch.28

… ►