6 Exponential, Logarithmic, Sine, and Cosine Integrals Applications 6.15 Sums 6.17 Physical Applications

§6.16 Mathematical Applications

Permalink:: http://dlmf.nist.gov/6.16

§6.16(i) The Gibbs Phenomenon
§6.16(ii) Number-Theoretic Significance of $\mathop{\mathrm{li}\/}\nolimits\!\left(x\right)$

§6.16(i) The Gibbs Phenomenon

Notes:: See Temme (1996b, pp. 181–182: the numerical value $1.089490\dots$ on p. 182 should be replaced by $1.1789\dots$ ). Gibbs reported this phenomenon in a letter to Nature, 59 (1899, p. 606). Figure 6.16.1 was produced at NIST.
Keywords:: Fourier-series expansions, Gibbs phenomenon, sine integrals
Referenced by:: §1.8(ii)
Permalink:: http://dlmf.nist.gov/6.16.i

Consider the Fourier series

6.16.1 $\mathop{\sin\/}\nolimits x+\tfrac{1}{3}\mathop{\sin\/}\nolimits\!\left(3x% \right)+\tfrac{1}{5}\mathop{\sin\/}\nolimits\!\left(5x\right)+\dots=\begin{% cases}\frac{1}{4}\pi,&0<x<\pi,\\ 0,&x=0,\\ -\frac{1}{4}\pi,&-\pi<x<0.\end{cases}$

Symbols:: $\mathop{\sin\/}\nolimits z$ : sine function and : real variable
Permalink:: http://dlmf.nist.gov/6.16.E1
Encodings:: TeX, pMML, png

The th partial sum is given by

6.16.2 $S_{n}(x)=\sum_{{k=0}}^{{n-1}}\frac{\mathop{\sin\/}\nolimits\!\left((2k+1)x% \right)}{2k+1}=\frac{1}{2}\int_{0}^{x}\frac{\mathop{\sin\/}\nolimits\!\left(2% nt\right)}{\mathop{\sin\/}\nolimits t}dt=\tfrac{1}{2}\mathop{\mathrm{Si}\/}% \nolimits\!\left(2nx\right)+R_{n}(x),$

Symbols:: : differential of , $\int$ : integral, $\mathop{\sin\/}\nolimits z$ : sine function, $\mathop{\mathrm{Si}\/}\nolimits\!\left(z\right)$ : sine integral, : real variable, : nonnegative integer, $S_{n}(x)$ : partial sum and $R_{n}(x)$ : remainder term
Permalink:: http://dlmf.nist.gov/6.16.E2
Encodings:: TeX, pMML, png

where

6.16.3 $R_{n}(x)=\frac{1}{2}\int_{0}^{x}\left(\frac{1}{\mathop{\sin\/}\nolimits t}-% \frac{1}{t}\right)\mathop{\sin\/}\nolimits\!\left(2nt\right)dt.$

Symbols:: : differential of , $\int$ : integral, $\mathop{\sin\/}\nolimits z$ : sine function, : real variable, : nonnegative integer and $R_{n}(x)$ : remainder term
Permalink:: http://dlmf.nist.gov/6.16.E3
Encodings:: TeX, pMML, png

By integration by parts

6.16.4 $R_{n}(x)=\mathop{O\/}\nolimits\!\left(n^{{-1}}\right),$ $n\to\infty$ ,

Symbols:: $\mathop{O\/}\nolimits\!\left(x\right)$ : order not exceeding, : real variable, : nonnegative integer and $R_{n}(x)$ : remainder term
Permalink:: http://dlmf.nist.gov/6.16.E4
Encodings:: TeX, pMML, png

uniformly for $x\in[-\pi,\pi]$ . Hence, if is fixed and $n\to\infty$ , then $S_{n}(x)\to\frac{1}{4}\pi$ , 0, or $-\frac{1}{4}\pi$ according as $0<x<\pi$ , , or $-\pi<x<0$ ; compare (6.2.14).

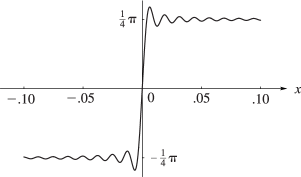
These limits are not approached uniformly, however. The first maximum of $\frac{1}{2}\mathop{\mathrm{Si}\/}\nolimits\!\left(x\right)$ for positive occurs at $x=\pi$ and equals $(1.1789\dots)\times\frac{1}{4}\pi$ ; compare Figure 6.3.2. Hence if $x=\pi/(2n)$ and $n\to\infty$ , then the limiting value of $S_{n}(x)$ overshoots $\frac{1}{4}\pi$ by approximately 18%. Similarly if $x=\pi/n$ , then the limiting value of $S_{n}(x)$ undershoots $\frac{1}{4}\pi$ by approximately 10%, and so on. Compare Figure 6.16.1.

This nonuniformity of convergence is an illustration of the Gibbs phenomenon. It occurs with Fourier-series expansions of all piecewise continuous functions. See Carslaw (1930) for additional graphs and information.

Figure 6.16.1: Graph of $S_{n}(x)$ ,

, $-0.1\leq x\leq 0.1$ , illustrating the Gibbs phenomenon.

Symbols:: : real variable, : nonnegative integer and $S_{n}(x)$ : partial sum
Referenced by:: §6.16(i), §6.16(i)
Permalink:: http://dlmf.nist.gov/6.16.F1
Encodings:: pdf, png

§6.16(ii) Number-Theoretic Significance of $\mathop{\mathrm{li}\/}\nolimits\!\left(x\right)$

Notes:: Figure 6.16.2 was produced at NIST.
Keywords:: logarithmic integral, prime numbers
Permalink:: http://dlmf.nist.gov/6.16.ii

If we assume Riemann’s hypothesis that all nonreal zeros of $\mathop{\zeta\/}\nolimits\!\left(s\right)$ have real part of $\tfrac{1}{2}$ (§25.10(i)), then

6.16.5 $\mathop{\mathrm{li}\/}\nolimits\!\left(x\right)-\pi(x)=\mathop{O\/}\nolimits\!% \left(\sqrt{x}\mathop{\ln\/}\nolimits x\right),$ $x\to\infty$ ,

Symbols:: $\mathop{O\/}\nolimits\!\left(x\right)$ : order not exceeding, $\mathop{\mathrm{li}\/}\nolimits\!\left(x\right)$ : logarithmic integral, $\mathop{\ln\/}\nolimits z$ : principal branch of logarithm function, : real variable and $\pi(x)$ : number of primes $\leq x$
A&S Ref:: 5.1.50
Permalink:: http://dlmf.nist.gov/6.16.E5
Encodings:: TeX, pMML, png

where $\pi(x)$ is the number of primes less than or equal to . Compare §27.12 and Figure 6.16.2. See also Bays and Hudson (2000).

Figure 6.16.2: The logarithmic integral $\mathop{\mathrm{li}\/}\nolimits\!\left(x\right)$ , together with vertical bars indicating the value of $\pi(x)$ for $x=10,20,\dots,1000$ .

Symbols:: $\mathop{\mathrm{li}\/}\nolimits\!\left(x\right)$ : logarithmic integral, : real variable and $\pi(x)$ : number of primes $\leq x$
Keywords:: logarithmic integral
Referenced by:: §6.16(ii), §6.16(ii), §6.3(i)
Permalink:: http://dlmf.nist.gov/6.16.F2
Encodings:: pdf, png

© 2010–2013 NIST / Privacy Policy / Disclaimer / Feedback; Version 1.0.6; Release date 2013-05-06 Math-Image version (See MathML) . A Printed Companionis available. 6.15 Sums 6.17 Physical Applications

§6.16 Mathematical Applications

Contents

§6.16(i) The Gibbs Phenomenon

§6.16(ii) Number-Theoretic Significance of

§6.16(ii) Number-Theoretic Significance of $\mathop{\mathrm{li}\/}\nolimits\!\left(x\right)$