§9.12 Scorer Functions

Keywords:: Scorer functions
Referenced by:: §2.4(v), ¶ ‣ §3.5(ix), §9.10(i)
Permalink:: http://dlmf.nist.gov/9.12

§9.12(i) Differential Equation
§9.12(ii) Graphs
§9.12(iii) Initial Values
§9.12(iv) Numerically Satisfactory Solutions
§9.12(v) Connection Formulas
§9.12(vi) Maclaurin Series
§9.12(vii) Integral Representations
§9.12(viii) Asymptotic Expansions
§9.12(ix) Zeros

§9.12(i) Differential Equation

Notes:: See Olver (1997b, pp. 430–431).
Defines:: $\mathop{\mathrm{Hi}\/}\nolimits\!\left(z\right)$ : Scorer function (inhomogeneous Airy function) and $\mathop{\mathrm{Gi}\/}\nolimits\!\left(z\right)$ : Scorer function (inhomogeneous Airy function)
Keywords:: Scorer functions
Referenced by:: §11.11(iii)
Permalink:: http://dlmf.nist.gov/9.12.i

9.12.1 $\frac{{d}^{2}w}{{dz}^{2}}-zw=\frac{1}{\pi}.$

Symbols:: $\frac{df}{dx}$ : derivative of with respect to , : complex variable and : function
Referenced by:: §9.12(i), §9.12(vii), §9.17(ii)
Permalink:: http://dlmf.nist.gov/9.12.E1
Encodings:: TeX, pMML, png

Solutions of this equation are the Scorer functions and can be found by the method of variation of parameters (§1.13(iii)). The general solution is given by

9.12.2 $w(z)=Aw_{1}(z)+Bw_{2}(z)+p(z),$

Symbols:: : complex variable, : function, : constant, : constant, $w_{1}$ : function, $w_{2}$ : function and : particular solution
Permalink:: http://dlmf.nist.gov/9.12.E2
Encodings:: TeX, pMML, png

where and are arbitrary constants, $w_{1}(z)$ and $w_{2}(z)$ are any two linearly independent solutions of Airy’s equation (9.2.1), and is any particular solution of (9.12.1). Standard particular solutions are

9.12.3

$-\mathop{\mathrm{Gi}\/}\nolimits\!\left(z\right)$ ,

$\mathop{\mathrm{Hi}\/}\nolimits\!\left(z\right)$ ,

$e^{{\mp 2\pi i/3}}\mathop{\mathrm{Hi}\/}\nolimits\!\left(ze^{{\mp 2\pi i/3}}\right)$ ,

Symbols:: $\mathop{\mathrm{Gi}\/}\nolimits\!\left(z\right)$ : Scorer function (inhomogeneous Airy function), $\mathop{\mathrm{Hi}\/}\nolimits\!\left(z\right)$ : Scorer function (inhomogeneous Airy function), : base of exponential function and : complex variable
Permalink:: http://dlmf.nist.gov/9.12.E3
Encodings:: TeX, TeX, TeX, pMML, pMML, pMML, png, png, png

where

9.12.4 $\mathop{\mathrm{Gi}\/}\nolimits\!\left(z\right)=\mathop{\mathrm{Bi}\/}% \nolimits\!\left(z\right)\int_{z}^{\infty}\mathop{\mathrm{Ai}\/}\nolimits\!% \left(t\right)dt+\mathop{\mathrm{Ai}\/}\nolimits\!\left(z\right)\int_{0}^{z}% \mathop{\mathrm{Bi}\/}\nolimits\!\left(t\right)dt,$

Symbols:: $\mathop{\mathrm{Ai}\/}\nolimits\!\left(z\right)$ : Airy function, $\mathop{\mathrm{Bi}\/}\nolimits\!\left(z\right)$ : Airy function, $\mathop{\mathrm{Gi}\/}\nolimits\!\left(z\right)$ : Scorer function (inhomogeneous Airy function), : differential of , $\int$ : integral and : complex variable
Referenced by:: §9.10(i)
Permalink:: http://dlmf.nist.gov/9.12.E4
Encodings:: TeX, pMML, png

9.12.5 $\mathop{\mathrm{Hi}\/}\nolimits\!\left(z\right)=\mathop{\mathrm{Bi}\/}% \nolimits\!\left(z\right)\int_{{-\infty}}^{z}\mathop{\mathrm{Ai}\/}\nolimits\!% \left(t\right)dt-\mathop{\mathrm{Ai}\/}\nolimits\!\left(z\right)\int_{{-\infty% }}^{z}\mathop{\mathrm{Bi}\/}\nolimits\!\left(t\right)dt.$

Symbols:: $\mathop{\mathrm{Ai}\/}\nolimits\!\left(z\right)$ : Airy function, $\mathop{\mathrm{Bi}\/}\nolimits\!\left(z\right)$ : Airy function, $\mathop{\mathrm{Hi}\/}\nolimits\!\left(z\right)$ : Scorer function (inhomogeneous Airy function), : differential of , $\int$ : integral and : complex variable
Permalink:: http://dlmf.nist.gov/9.12.E5
Encodings:: TeX, pMML, png

$\mathop{\mathrm{Gi}\/}\nolimits\!\left(z\right)$ and $\mathop{\mathrm{Hi}\/}\nolimits\!\left(z\right)$ are entire functions of .

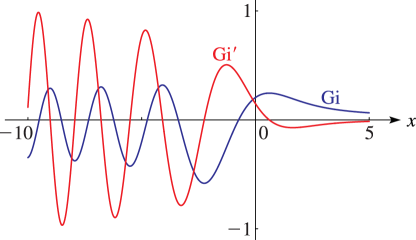
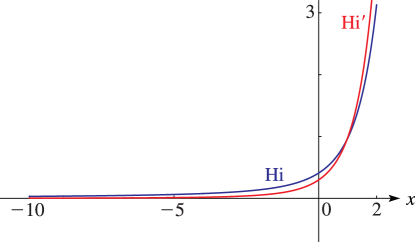
§9.12(ii) Graphs

Notes:: These graphs were produced by NIST.
Keywords:: Scorer functions
Permalink:: http://dlmf.nist.gov/9.12.ii

See Figures 9.12.1 and 9.12.2.

Figure 9.12.1: $\mathop{\mathrm{Gi}\/}\nolimits\!\left(x\right)$ , ${\mathop{\mathrm{Gi}\/}\nolimits^{{\prime}}}\!\left(x\right)$ .

Symbols:: $\mathop{\mathrm{Gi}\/}\nolimits\!\left(z\right)$ : Scorer function (inhomogeneous Airy function) and : real variable
Referenced by:: §9.12(ii), §9.12(ix)
Permalink:: http://dlmf.nist.gov/9.12.F1
Encodings:: pdf, png

Figure 9.12.2: $\mathop{\mathrm{Hi}\/}\nolimits\!\left(x\right)$ , ${\mathop{\mathrm{Hi}\/}\nolimits^{{\prime}}}\!\left(x\right)$ .

Symbols:: $\mathop{\mathrm{Hi}\/}\nolimits\!\left(z\right)$ : Scorer function (inhomogeneous Airy function) and : real variable
Referenced by:: §9.12(ii), §9.12(ix)
Permalink:: http://dlmf.nist.gov/9.12.F2
Encodings:: pdf, png

§9.12(iii) Initial Values

Notes:: See Olver (1997b, p. 431).
Keywords:: Scorer functions
Referenced by:: §9.12(v), §9.12(vii)
Permalink:: http://dlmf.nist.gov/9.12.iii

9.12.6 $\mathop{\mathrm{Gi}\/}\nolimits\!\left(0\right)=\tfrac{1}{2}\mathop{\mathrm{Hi% }\/}\nolimits\!\left(0\right)=\tfrac{1}{3}\mathop{\mathrm{Bi}\/}\nolimits\!% \left(0\right)={1\Big/\!\left(3^{{7/6}}\mathop{\Gamma\/}\nolimits\!\left(% \tfrac{2}{3}\right)\right)=0.20497\;55424\ldots,}$

Symbols:: $\mathop{\mathrm{Bi}\/}\nolimits\!\left(z\right)$ : Airy function, $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, $\mathop{\mathrm{Gi}\/}\nolimits\!\left(z\right)$ : Scorer function (inhomogeneous Airy function) and $\mathop{\mathrm{Hi}\/}\nolimits\!\left(z\right)$ : Scorer function (inhomogeneous Airy function)
Permalink:: http://dlmf.nist.gov/9.12.E6
Encodings:: TeX, pMML, png

9.12.7 ${\mathop{\mathrm{Gi}\/}\nolimits^{{\prime}}}\!\left(0\right)=\tfrac{1}{2}{% \mathop{\mathrm{Hi}\/}\nolimits^{{\prime}}}\!\left(0\right)=\tfrac{1}{3}{% \mathop{\mathrm{Bi}\/}\nolimits^{{\prime}}}\!\left(0\right)=1\Big/\left(3^{{5/% 6}}\mathop{\Gamma\/}\nolimits\!\left(\tfrac{1}{3}\right)\right)=0.14942\;94524\ldots.$

Symbols:: $\mathop{\mathrm{Bi}\/}\nolimits\!\left(z\right)$ : Airy function, $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, $\mathop{\mathrm{Gi}\/}\nolimits\!\left(z\right)$ : Scorer function (inhomogeneous Airy function) and $\mathop{\mathrm{Hi}\/}\nolimits\!\left(z\right)$ : Scorer function (inhomogeneous Airy function)
Permalink:: http://dlmf.nist.gov/9.12.E7
Encodings:: TeX, pMML, png

§9.12(iv) Numerically Satisfactory Solutions

Notes:: Refer to the asymptotic expansions given in §§9.7(ii) and 9.12(viii).
Keywords:: Scorer functions
Permalink:: http://dlmf.nist.gov/9.12.iv

$-\mathop{\mathrm{Gi}\/}\nolimits\!\left(x\right)$ is a numerically satisfactory companion to the complementary functions $\mathop{\mathrm{Ai}\/}\nolimits\!\left(x\right)$ and $\mathop{\mathrm{Bi}\/}\nolimits\!\left(x\right)$ on the interval $0\leq x<\infty$ . $\mathop{\mathrm{Hi}\/}\nolimits\!\left(x\right)$ is a numerically satisfactory companion to $\mathop{\mathrm{Ai}\/}\nolimits\!\left(x\right)$ and $\mathop{\mathrm{Bi}\/}\nolimits\!\left(x\right)$ on the interval $-\infty<x\leq 0$ .

In $\Complex$ , numerically satisfactory sets of solutions are given by

9.12.8 $-\mathop{\mathrm{Gi}\/}\nolimits\!\left(z\right),\mathop{\mathrm{Ai}\/}% \nolimits\!\left(z\right),\mathop{\mathrm{Bi}\/}\nolimits\!\left(z\right),$ $|\mathop{\mathrm{ph}\/}\nolimits z|\leq\tfrac{1}{3}\pi$ ,

Symbols:: $\mathop{\mathrm{Ai}\/}\nolimits\!\left(z\right)$ : Airy function, $\mathop{\mathrm{Bi}\/}\nolimits\!\left(z\right)$ : Airy function, $\mathop{\mathrm{Gi}\/}\nolimits\!\left(z\right)$ : Scorer function (inhomogeneous Airy function), $\mathop{\mathrm{ph}\/}\nolimits$ : phase and : complex variable
Permalink:: http://dlmf.nist.gov/9.12.E8
Encodings:: TeX, pMML, png

9.12.9 $\mathop{\mathrm{Hi}\/}\nolimits\!\left(z\right),\mathop{\mathrm{Ai}\/}% \nolimits\!\left(ze^{{-2\pi i/3}}\right),\mathop{\mathrm{Ai}\/}\nolimits\!% \left(ze^{{2\pi i/3}}\right),$ $|\mathop{\mathrm{ph}\/}\nolimits(-z)|\leq\tfrac{2}{3}\pi$ ,

Symbols:: $\mathop{\mathrm{Ai}\/}\nolimits\!\left(z\right)$ : Airy function, $\mathop{\mathrm{Hi}\/}\nolimits\!\left(z\right)$ : Scorer function (inhomogeneous Airy function), : base of exponential function, $\mathop{\mathrm{ph}\/}\nolimits$ : phase and : complex variable
Permalink:: http://dlmf.nist.gov/9.12.E9
Encodings:: TeX, pMML, png

and

9.12.10 $e^{{\mp 2\pi i/3}}\mathop{\mathrm{Hi}\/}\nolimits\!\left(ze^{{\mp 2\pi i/3}}% \right),\mathop{\mathrm{Ai}\/}\nolimits\!\left(z\right),\mathop{\mathrm{Ai}\/}% \nolimits\!\left(ze^{{\pm 2\pi i/3}}\right),$ $-\pi\leq\pm\mathop{\mathrm{ph}\/}\nolimits z\leq\tfrac{1}{3}\pi$ .

Symbols:: $\mathop{\mathrm{Ai}\/}\nolimits\!\left(z\right)$ : Airy function, $\mathop{\mathrm{Hi}\/}\nolimits\!\left(z\right)$ : Scorer function (inhomogeneous Airy function), : base of exponential function, $\mathop{\mathrm{ph}\/}\nolimits$ : phase and : complex variable
Permalink:: http://dlmf.nist.gov/9.12.E10
Encodings:: TeX, pMML, png

§9.12(v) Connection Formulas

Notes:: These results can be verified with the aid of §§9.2(ii) and 9.12(iii).
Keywords:: Scorer functions
Permalink:: http://dlmf.nist.gov/9.12.v

9.12.11 $\mathop{\mathrm{Gi}\/}\nolimits\!\left(z\right)+\mathop{\mathrm{Hi}\/}% \nolimits\!\left(z\right)=\mathop{\mathrm{Bi}\/}\nolimits\!\left(z\right),$

Symbols:: $\mathop{\mathrm{Bi}\/}\nolimits\!\left(z\right)$ : Airy function, $\mathop{\mathrm{Gi}\/}\nolimits\!\left(z\right)$ : Scorer function (inhomogeneous Airy function), $\mathop{\mathrm{Hi}\/}\nolimits\!\left(z\right)$ : Scorer function (inhomogeneous Airy function) and : complex variable
Referenced by:: §9.10(i), ¶ ‣ §9.12(viii), §9.12(vi), §9.12(vii)
Permalink:: http://dlmf.nist.gov/9.12.E11
Encodings:: TeX, pMML, png

9.12.12 $\mathop{\mathrm{Gi}\/}\nolimits\!\left(z\right)=\tfrac{1}{2}e^{{\pi i/3}}% \mathop{\mathrm{Hi}\/}\nolimits\!\left(ze^{{-2\pi i/3}}\right)+\tfrac{1}{2}e^{% {-\pi i/3}}\mathop{\mathrm{Hi}\/}\nolimits\!\left(ze^{{2\pi i/3}}\right),$

Symbols:: $\mathop{\mathrm{Gi}\/}\nolimits\!\left(z\right)$ : Scorer function (inhomogeneous Airy function), $\mathop{\mathrm{Hi}\/}\nolimits\!\left(z\right)$ : Scorer function (inhomogeneous Airy function), : base of exponential function and : complex variable
Referenced by:: §9.12(viii)
Permalink:: http://dlmf.nist.gov/9.12.E12
Encodings:: TeX, pMML, png

9.12.13 $\mathop{\mathrm{Gi}\/}\nolimits\!\left(z\right)=e^{{\mp\pi i/3}}\mathop{% \mathrm{Hi}\/}\nolimits\!\left(ze^{{\pm 2\pi i/3}}\right)\pm i\mathop{\mathrm{% Ai}\/}\nolimits\!\left(z\right),$

Symbols:: $\mathop{\mathrm{Ai}\/}\nolimits\!\left(z\right)$ : Airy function, $\mathop{\mathrm{Gi}\/}\nolimits\!\left(z\right)$ : Scorer function (inhomogeneous Airy function), $\mathop{\mathrm{Hi}\/}\nolimits\!\left(z\right)$ : Scorer function (inhomogeneous Airy function), : base of exponential function and : complex variable
Permalink:: http://dlmf.nist.gov/9.12.E13
Encodings:: TeX, pMML, png

9.12.14 $\mathop{\mathrm{Hi}\/}\nolimits\!\left(z\right)=e^{{\pm 2\pi i/3}}\mathop{% \mathrm{Hi}\/}\nolimits\!\left(ze^{{\pm 2\pi i/3}}\right)+2e^{{\mp\pi i/6}}% \mathop{\mathrm{Ai}\/}\nolimits\!\left(ze^{{\mp 2\pi i/3}}\right).$

Symbols:: $\mathop{\mathrm{Ai}\/}\nolimits\!\left(z\right)$ : Airy function, $\mathop{\mathrm{Hi}\/}\nolimits\!\left(z\right)$ : Scorer function (inhomogeneous Airy function), : base of exponential function and : complex variable
Referenced by:: ¶ ‣ §9.12(viii)
Permalink:: http://dlmf.nist.gov/9.12.E14
Encodings:: TeX, pMML, png

§9.12(vi) Maclaurin Series

Notes:: For (9.12.17) expand the integral in (9.12.20) in powers of and integrate term-by-term by means of (5.2.1). For (9.12.15) substitute into (9.12.11) by means of (9.12.17), (9.4.3), (9.2.5), (9.2.6), and use (5.5.3). For (9.12.16) and (9.12.18) differentiate.
Keywords:: Scorer functions
Referenced by:: §9.17(i)
Permalink:: http://dlmf.nist.gov/9.12.vi

9.12.15 $\mathop{\mathrm{Gi}\/}\nolimits\!\left(z\right)=\frac{3^{{-2/3}}}{\pi}\*\sum_{% {k=0}}^{{\infty}}\mathop{\cos\/}\nolimits\!\left(\frac{2k-1}{3}\pi\right)% \mathop{\Gamma\/}\nolimits\!\left(\frac{k+1}{3}\right)\frac{(3^{{1/3}}z)^{k}}{% k!},$

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, $\mathop{\mathrm{Gi}\/}\nolimits\!\left(z\right)$ : Scorer function (inhomogeneous Airy function), $\mathop{\cos\/}\nolimits z$ : cosine function, : : factorial, : nonnegative integer and : complex variable
Referenced by:: §9.12(vi)
Permalink:: http://dlmf.nist.gov/9.12.E15
Encodings:: TeX, pMML, png

9.12.16 ${\mathop{\mathrm{Gi}\/}\nolimits^{{\prime}}}\!\left(z\right)=\frac{3^{{-1/3}}}% {\pi}\*\sum_{{k=0}}^{{\infty}}\mathop{\cos\/}\nolimits\!\left(\frac{2k+1}{3}% \pi\right)\mathop{\Gamma\/}\nolimits\!\left(\frac{k+2}{3}\right)\frac{(3^{{1/3% }}z)^{k}}{k!}.$

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, $\mathop{\mathrm{Gi}\/}\nolimits\!\left(z\right)$ : Scorer function (inhomogeneous Airy function), $\mathop{\cos\/}\nolimits z$ : cosine function, : : factorial, : nonnegative integer and : complex variable
Referenced by:: §9.12(vi)
Permalink:: http://dlmf.nist.gov/9.12.E16
Encodings:: TeX, pMML, png

9.12.17 $\mathop{\mathrm{Hi}\/}\nolimits\!\left(z\right)=\frac{3^{{-2/3}}}{\pi}\sum_{{k% =0}}^{{\infty}}\mathop{\Gamma\/}\nolimits\!\left(\frac{k+1}{3}\right)\frac{(3^% {{1/3}}z)^{k}}{k!},$

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, $\mathop{\mathrm{Hi}\/}\nolimits\!\left(z\right)$ : Scorer function (inhomogeneous Airy function), : : factorial, : nonnegative integer and : complex variable
Referenced by:: §9.12(vi)
Permalink:: http://dlmf.nist.gov/9.12.E17
Encodings:: TeX, pMML, png

9.12.18 ${\mathop{\mathrm{Hi}\/}\nolimits^{{\prime}}}\!\left(z\right)=\frac{3^{{-1/3}}}% {\pi}\sum_{{k=0}}^{{\infty}}\mathop{\Gamma\/}\nolimits\!\left(\frac{k+2}{3}% \right)\frac{(3^{{1/3}}z)^{k}}{k!}.$

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, $\mathop{\mathrm{Hi}\/}\nolimits\!\left(z\right)$ : Scorer function (inhomogeneous Airy function), : : factorial, : nonnegative integer and : complex variable
Referenced by:: §9.12(vi)
Permalink:: http://dlmf.nist.gov/9.12.E18
Encodings:: TeX, pMML, png

§9.12(vii) Integral Representations

Notes:: (9.12.20) can be verified by showing that the right-hand side satisfies the differential equation (9.12.1) and the initial conditions given in §9.12(iii). For (9.12.19) combine (9.5.3) and (9.12.11). For (9.12.21), see Lee (1980). For (9.12.22), (9.12.23) see Gordon (1970, Appendix A). For (9.12.24) see Exton (1983).
Keywords:: Scorer functions, integrals of modified Bessel functions
Permalink:: http://dlmf.nist.gov/9.12.vii

9.12.19 $\mathop{\mathrm{Gi}\/}\nolimits\!\left(x\right)=\frac{1}{\pi}\int_{0}^{{\infty% }}\mathop{\sin\/}\nolimits\!\left(\tfrac{1}{3}t^{3}+xt\right)dt,$ $x\in\Real$ .

Symbols:: $\mathop{\mathrm{Gi}\/}\nolimits\!\left(z\right)$ : Scorer function (inhomogeneous Airy function), : differential of , $\in$ : element of, $\int$ : integral, $\Real$ : real line (excluding infinity), $\mathop{\sin\/}\nolimits z$ : sine function and : real variable
Referenced by:: §9.12(vii)
Permalink:: http://dlmf.nist.gov/9.12.E19
Encodings:: TeX, pMML, png

9.12.20 $\mathop{\mathrm{Hi}\/}\nolimits\!\left(z\right)=\frac{1}{\pi}\int_{0}^{{\infty% }}\mathop{\exp\/}\nolimits\!\left(-\tfrac{1}{3}t^{3}+zt\right)dt,$

Symbols:: $\mathop{\mathrm{Hi}\/}\nolimits\!\left(z\right)$ : Scorer function (inhomogeneous Airy function), : differential of , $\mathop{\exp\/}\nolimits z$ : exponential function, $\int$ : integral and : complex variable
Referenced by:: §9.12(vi), §9.12(vii), §9.12(viii)
Permalink:: http://dlmf.nist.gov/9.12.E20
Encodings:: TeX, pMML, png

9.12.21 $\mathop{\mathrm{Gi}\/}\nolimits\!\left(z\right)=-\frac{1}{\pi}\int_{0}^{{% \infty}}\mathop{\exp\/}\nolimits\!\left(-\tfrac{1}{3}t^{3}-\tfrac{1}{2}zt% \right)\mathop{\cos\/}\nolimits\!\left(\tfrac{1}{2}\sqrt{3}zt+\tfrac{2}{3}\pi% \right)dt.$

Symbols:: $\mathop{\mathrm{Gi}\/}\nolimits\!\left(z\right)$ : Scorer function (inhomogeneous Airy function), $\mathop{\cos\/}\nolimits z$ : cosine function, : differential of , $\mathop{\exp\/}\nolimits z$ : exponential function, $\int$ : integral and : complex variable
Referenced by:: §9.12(vii)
Permalink:: http://dlmf.nist.gov/9.12.E21
Encodings:: TeX, pMML, png

If $\zeta=\tfrac{2}{3}z^{{3/2}}$ or $\tfrac{2}{3}x^{{3/2}}$ , and $\mathop{K_{{1/3}}\/}\nolimits$ is the modified Bessel function (§10.25(ii)), then

9.12.22 $\mathop{\mathrm{Hi}\/}\nolimits\!\left(-z\right)=\frac{4z^{2}}{3^{{3/2}}\pi^{2% }}\int_{0}^{{\infty}}\frac{\mathop{K_{{1/3}}\/}\nolimits\!\left(t\right)}{% \zeta^{2}+t^{2}}dt,$ $|\mathop{\mathrm{ph}\/}\nolimits z|<\tfrac{1}{3}\pi$ ,

Symbols:: $\mathop{\mathrm{Hi}\/}\nolimits\!\left(z\right)$ : Scorer function (inhomogeneous Airy function), : differential of , $\int$ : integral, $\mathop{K_{{\nu}}\/}\nolimits\!\left(z\right)$ : modified Bessel function, $\mathop{\mathrm{ph}\/}\nolimits$ : phase, : complex variable and $\zeta$ : variable
Referenced by:: §9.12(vii)
Permalink:: http://dlmf.nist.gov/9.12.E22
Encodings:: TeX, pMML, png

9.12.23 $\mathop{\mathrm{Gi}\/}\nolimits\!\left(x\right)=\frac{4x^{2}}{3^{{3/2}}\pi^{2}% }\pvint_{0}^{{\infty}}\frac{\mathop{K_{{1/3}}\/}\nolimits\!\left(t\right)}{% \zeta^{2}-t^{2}}dt,$

Symbols:: $\mathop{\mathrm{Gi}\/}\nolimits\!\left(z\right)$ : Scorer function (inhomogeneous Airy function), : differential of , $\mathop{K_{{\nu}}\/}\nolimits\!\left(z\right)$ : modified Bessel function, $\pvint_{a}^{b}$ : Cauchy principal value, : real variable and $\zeta$ : variable
Referenced by:: §9.12(vii)
Permalink:: http://dlmf.nist.gov/9.12.E23
Encodings:: TeX, pMML, png

where the last integral is a Cauchy principal value (§1.4(v)).

¶ Mellin–Barnes Type Integral

Keywords:: Scorer functions

9.12.24 $\mathop{\mathrm{Hi}\/}\nolimits\!\left(z\right)=\frac{3^{{-2/3}}}{2\pi^{2}i}% \int_{{-i\infty}}^{{i\infty}}\mathop{\Gamma\/}\nolimits\!\left(\tfrac{1}{3}+% \tfrac{1}{3}t\right)\mathop{\Gamma\/}\nolimits\!\left(-t\right)(3^{{1/3}}e^{{% \pi i}}z)^{t}dt,$

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, $\mathop{\mathrm{Hi}\/}\nolimits\!\left(z\right)$ : Scorer function (inhomogeneous Airy function), : differential of , : base of exponential function, $\int$ : integral and : complex variable
Referenced by:: §9.12(vii)
Permalink:: http://dlmf.nist.gov/9.12.E24
Encodings:: TeX, pMML, png

where the integration contour separates the poles of $\mathop{\Gamma\/}\nolimits\!\left(\tfrac{1}{3}+\tfrac{1}{3}t\right)$ from those of $\mathop{\Gamma\/}\nolimits\!\left(-t\right)$ .

§9.12(viii) Asymptotic Expansions

Notes:: For (9.12.25), (9.12.27) see Olver (1997b, pp. 431–432). For (9.12.26), (9.12.28) refer to §2.1(ii). Except for the constant term, (9.12.31) can be verified by termwise integration of (9.12.27). To evaluate the constant term replace by ( $\leq 0$ ) in (9.12.20) and integrate (§1.5(v)) to obtain $\pi\int_{0}^{x}\mathop{\mathrm{Hi}\/}\nolimits\!\left(-t\right)dt=\int_{0}^{% \infty}(1-e^{{-xt}})e^{{-\frac{1}{3}t^{3}}}t^{{-1}}dt$ . Next, integrate the right-hand side of this equation by parts—integrating the factor $t^{{-1}}$ and differentiating the rest. As $x\to\infty$ the asymptotic expansions of $\int_{0}^{\infty}xe^{{-xt}}e^{{-\frac{1}{3}t^{3}}}(\mathop{\ln\/}\nolimits t)dt$ and $\int_{0}^{\infty}e^{{-xt}}t^{2}e^{{-\frac{1}{3}t^{3}}}(\mathop{\ln\/}\nolimits t% )dt$ follow from (2.3.9). Also, $\int_{0}^{\infty}t^{2}e^{{-\frac{1}{3}t^{3}}}(\mathop{\ln\/}\nolimits t)dt$ can be found by replacing $\frac{1}{3}t^{3}$ by and referring to the first of (5.9.18). For (9.12.30) integrate (9.12.25) and obtain the constant term by combining (9.12.12) and (9.12.31). (Equations (9.12.30) and (9.12.31) first appeared in Rothman (1954a). As noted in this reference these results were derived by the author of the present DLMF chapter, but the proof was not included.)
Keywords:: Scorer functions
Referenced by:: §9.12(iv), §9.17(i)
Permalink:: http://dlmf.nist.gov/9.12.viii

¶ Functions and Derivatives

As $z\to\infty$ , and with $\delta$ denoting an arbitrary small positive constant,

9.12.25 $\mathop{\mathrm{Gi}\/}\nolimits\!\left(z\right)\sim\frac{1}{\pi z}\sum_{{k=0}}% ^{{\infty}}\frac{(3k)!}{k!(3z^{3})^{k}},$ $|\mathop{\mathrm{ph}\/}\nolimits z|\leq\tfrac{1}{3}\pi-\delta$ ,

Symbols:: $\mathop{\mathrm{Gi}\/}\nolimits\!\left(z\right)$ : Scorer function (inhomogeneous Airy function), : : factorial, $\mathop{\mathrm{ph}\/}\nolimits$ : phase, $\sim$ : asymptotic equality, : nonnegative integer, : complex variable and $\delta$ : small positive constant
Referenced by:: §9.12(viii)
Permalink:: http://dlmf.nist.gov/9.12.E25
Encodings:: TeX, pMML, png

9.12.26 ${\mathop{\mathrm{Gi}\/}\nolimits^{{\prime}}}\!\left(z\right)\sim-\frac{1}{\pi z% ^{2}}\sum_{{k=0}}^{{\infty}}\frac{(3k+1)!}{k!(3z^{3})^{k}},$ $|\mathop{\mathrm{ph}\/}\nolimits z|\leq\tfrac{1}{3}\pi-\delta$ .

Symbols:: $\mathop{\mathrm{Gi}\/}\nolimits\!\left(z\right)$ : Scorer function (inhomogeneous Airy function), : : factorial, $\mathop{\mathrm{ph}\/}\nolimits$ : phase, $\sim$ : asymptotic equality, : nonnegative integer, : complex variable and $\delta$ : small positive constant
Referenced by:: §9.12(viii)
Permalink:: http://dlmf.nist.gov/9.12.E26
Encodings:: TeX, pMML, png

9.12.27 $\mathop{\mathrm{Hi}\/}\nolimits\!\left(z\right)\sim-\frac{1}{\pi z}\sum_{{k=0}% }^{{\infty}}\frac{(3k)!}{k!(3z^{3})^{k}},$ $|\mathop{\mathrm{ph}\/}\nolimits(-z)|\leq\tfrac{2}{3}\pi-\delta$ ,

Symbols:: $\mathop{\mathrm{Hi}\/}\nolimits\!\left(z\right)$ : Scorer function (inhomogeneous Airy function), : : factorial, $\mathop{\mathrm{ph}\/}\nolimits$ : phase, $\sim$ : asymptotic equality, : nonnegative integer, : complex variable and $\delta$ : small positive constant
Referenced by:: §9.12(viii)
Permalink:: http://dlmf.nist.gov/9.12.E27
Encodings:: TeX, pMML, png

9.12.28 ${\mathop{\mathrm{Hi}\/}\nolimits^{{\prime}}}\!\left(z\right)\sim\frac{1}{\pi z% ^{2}}\sum_{{k=0}}^{{\infty}}\frac{(3k+1)!}{k!(3z^{3})^{k}},$ $|\mathop{\mathrm{ph}\/}\nolimits(-z)|\leq\tfrac{2}{3}\pi-\delta$ .

Symbols:: $\mathop{\mathrm{Hi}\/}\nolimits\!\left(z\right)$ : Scorer function (inhomogeneous Airy function), : : factorial, $\mathop{\mathrm{ph}\/}\nolimits$ : phase, $\sim$ : asymptotic equality, : nonnegative integer, : complex variable and $\delta$ : small positive constant
Referenced by:: §9.12(viii)
Permalink:: http://dlmf.nist.gov/9.12.E28
Encodings:: TeX, pMML, png

For other phase ranges combine these results with the connection formulas (9.12.11)–(9.12.14) and the asymptotic expansions given in §9.7. For example, with the notation of §9.7(i).

9.12.29 $\mathop{\mathrm{Hi}\/}\nolimits\!\left(z\right)\sim-\frac{1}{\pi z}\sum_{{k=0}% }^{{\infty}}\frac{(3k)!}{k!(3z^{3})^{k}}+\frac{e^{\zeta}}{\sqrt{\pi}z^{{1/4}}}% \sum_{{k=0}}^{{\infty}}\frac{u_{k}}{\zeta^{k}},$ $|\mathop{\mathrm{ph}\/}\nolimits z|\leq\pi-\delta$ .

Symbols:: $\mathop{\mathrm{Hi}\/}\nolimits\!\left(z\right)$ : Scorer function (inhomogeneous Airy function), : base of exponential function, : : factorial, $\mathop{\mathrm{ph}\/}\nolimits$ : phase, $\sim$ : asymptotic equality, : nonnegative integer, : complex variable, $\delta$ : small positive constant, $\zeta(z)$ : change of variable and $u_{s}$ : expansion coefficient
Permalink:: http://dlmf.nist.gov/9.12.E29
Encodings:: TeX, pMML, png

¶ Integrals

Keywords:: Scorer functions, integrals

9.12.30 $\int_{0}^{z}\mathop{\mathrm{Gi}\/}\nolimits\!\left(t\right)dt\sim\frac{1}{\pi}% \mathop{\ln\/}\nolimits z+\frac{2\gamma+\mathop{\ln\/}\nolimits 3}{3\pi}-\frac% {1}{\pi}\sum_{{k=1}}^{{\infty}}\frac{(3k-1)!}{k!(3z^{3})^{k}},$ $|\mathop{\mathrm{ph}\/}\nolimits z|\leq\tfrac{1}{3}\pi-\delta$ .

Symbols:: $\EulerConstant$ : Euler’s constant, $\mathop{\mathrm{Gi}\/}\nolimits\!\left(z\right)$ : Scorer function (inhomogeneous Airy function), : differential of , : : factorial, $\int$ : integral, $\mathop{\ln\/}\nolimits z$ : principal branch of logarithm function, $\mathop{\mathrm{ph}\/}\nolimits$ : phase, $\sim$ : asymptotic equality, : nonnegative integer, : complex variable and $\delta$ : small positive constant
Referenced by:: §9.12(viii)
Permalink:: http://dlmf.nist.gov/9.12.E30
Encodings:: TeX, pMML, png

9.12.31 $\int_{0}^{z}\mathop{\mathrm{Hi}\/}\nolimits\!\left(-t\right)dt\sim\frac{1}{\pi% }\mathop{\ln\/}\nolimits z+\frac{2\gamma+\mathop{\ln\/}\nolimits 3}{3\pi}+% \frac{1}{\pi}\sum_{{k=1}}^{{\infty}}(-1)^{{k-1}}\frac{(3k-1)!}{k!(3z^{3})^{k}},$ $|\mathop{\mathrm{ph}\/}\nolimits z|\leq\tfrac{2}{3}\pi-\delta$ ,

Symbols:: $\EulerConstant$ : Euler’s constant, $\mathop{\mathrm{Hi}\/}\nolimits\!\left(z\right)$ : Scorer function (inhomogeneous Airy function), : differential of , : : factorial, $\int$ : integral, $\mathop{\ln\/}\nolimits z$ : principal branch of logarithm function, $\mathop{\mathrm{ph}\/}\nolimits$ : phase, $\sim$ : asymptotic equality, : nonnegative integer, : complex variable and $\delta$ : small positive constant
Referenced by:: §9.12(viii)
Permalink:: http://dlmf.nist.gov/9.12.E31
Encodings:: TeX, pMML, png

where $\gamma$ is Euler’s constant (§5.2(ii)).

§9.12(ix) Zeros

Keywords:: Scorer functions
Permalink:: http://dlmf.nist.gov/9.12.ix

All zeros, real or complex, of $\mathop{\mathrm{Gi}\/}\nolimits\!\left(z\right)$ and $\mathop{\mathrm{Hi}\/}\nolimits\!\left(z\right)$ are simple.

Neither $\mathop{\mathrm{Hi}\/}\nolimits\!\left(z\right)$ nor ${\mathop{\mathrm{Hi}\/}\nolimits^{{\prime}}}\!\left(z\right)$ has real zeros.

$\mathop{\mathrm{Gi}\/}\nolimits\!\left(z\right)$ has no nonnegative real zeros and ${\mathop{\mathrm{Gi}\/}\nolimits^{{\prime}}}\!\left(z\right)$ has exactly one nonnegative real zero, given by $z=0.60907\;54170\;7\ldots$ . Both $\mathop{\mathrm{Gi}\/}\nolimits\!\left(z\right)$ and ${\mathop{\mathrm{Gi}\/}\nolimits^{{\prime}}}\!\left(z\right)$ have an infinity of negative real zeros, and they are interlaced.

For the above properties and further results, including the distribution of complex zeros, asymptotic approximations for the numerically large real or complex zeros, and numerical tables see Gil et al. (2003c).

For graphical illustration of the real zeros see Figures 9.12.1 and 9.12.2.

© 2010–2013 NIST / Privacy Policy / Disclaimer / Feedback; Version 1.0.6; Release date 2013-05-06 Math-Image version (See MathML) . A Printed Companionis available. 9.11 Products 9.13 Generalized Airy Functions