inverse Jacobian elliptic functions

SearchAdvancedHelp

(0.008 seconds)

11—17 of 17 matching pages

11: 20.11 Generalizations and Analogs

… ►If both $m,n$ are positive, then $G(m,n)$ allows inversion of its arguments as a modular transformation (compare (23.15.3) and (23.15.4)): … ►As in §20.11(ii), the modulus $k$ of elliptic integrals (§19.2(ii)), Jacobian elliptic functions (§22.2), and Weierstrass elliptic functions (§23.6(ii)) can be expanded in $q$-series via (20.9.1). …This is Jacobi’s inversion problem of §20.9(ii). … ►Each provides an extension of Jacobi’s inversion problem. …

12: 22.10 Maclaurin Series

… ►

§22.10(i) Maclaurin Series in $z$

… ►The full expansions converge when . ►

§22.10(ii) Maclaurin Series in $k$ and $k^{\prime }$

… ►Further terms may be derived from the differential equations (22.13.13), (22.13.14), (22.13.15), or from the integral representations of the inverse functions in §22.15(ii). …

13: 22.2 Definitions

§22.2 Definitions

… ►Inversely, … ►As a function of $z$, with fixed $k$, each of the 12 Jacobian elliptic functions is doubly periodic, having two periods whose ratio is not real. … … ►The Jacobian functions are related in the following way. …

14: 19.10 Relations to Other Functions

§19.10 Relations to Other Functions

►

§19.10(i) Theta and Elliptic Functions

►For relations of Legendre’s integrals to theta functions, Jacobian functions, and Weierstrass functions, see §§20.9(i), 22.15(ii), and 23.6(iv), respectively. … ►

§19.10(ii) Elementary Functions

… ►For relations to the Gudermannian function $\mathrm{gd}\left(x\right)$ and its inverse ${\mathrm{gd}}^{-1}\left(x\right)$ (§4.23(viii)), see (19.6.8) and …

15: Errata

… ►

The wording was changed to make the integration variable more apparent.

… ►

This figure was rescaled, with symmetry lines added, to make evident the symmetry due to the inverse relationship between the two functions.

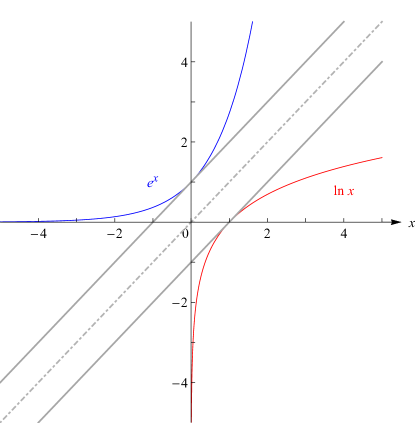
Reported 2015-11-12 by James W. Pitman.

… ►

These equations were rewritten with the modulus (second argument) of the Jacobian elliptic function defined explicitly in the preceding line of text.

… ►

22.19.2 $$\sin \left(\frac{1}{2}\theta (t)\right)=\sin \left(\frac{1}{2}\alpha \right)\mathrm{sn}(t+K,\sin \left(\frac{1}{2}\alpha \right))$$

Originally the first argument to the function $\mathrm{sn}$ was given incorrectly as $t$. The correct argument is $t+K$.

Reported 2014-03-05 by Svante Janson.

… ►

Originally a minus sign was missing in the entries for $\mathrm{cd}u$ and $\mathrm{dc}u$ in the second column (headed $z+K+i{K}^{\prime }$). The correct entries are $-k^{-1}\mathrm{ns}z$ and $-k\mathrm{sn}z$. Note: These entries appear online but not in the published print edition. More specifically, Table 22.4.3 in the published print edition is restricted to the three Jacobian elliptic functions $\mathrm{sn},\mathrm{cn},\mathrm{dn}$, whereas Table 22.4.3 covers all 12 Jacobian elliptic functions.

	$u$
	$z+K$	$z+K+\mathrm{i}{K}^{\prime }$	$z+\mathrm{i}{K}^{\prime }$	$z+2K$	$z+2K+2\mathrm{i}{K}^{\prime }$	$z+2\mathrm{i}{K}^{\prime }$
$\mathrm{⋮}$
$\mathrm{cd}u$	$-\mathrm{sn}z$	$-k^{-1}\mathrm{ns}z$	$k^{-1}\mathrm{dc}z$	$-\mathrm{cd}z$	$-\mathrm{cd}z$	$\mathrm{cd}z$
$\mathrm{⋮}$
$\mathrm{dc}u$	$-\mathrm{ns}z$	$-k\mathrm{sn}z$	$k\mathrm{cd}z$	$-\mathrm{dc}z$	$-\mathrm{dc}z$	$\mathrm{dc}z$
$\mathrm{⋮}$

Reported 2014-02-28 by Svante Janson.

…

16: Bibliography W

… ►

Evaluating elliptic functions and their inverses. Comput. Math. Appl. 39 (3-4), pp. 131–136.

ⓘ

External Links:

ISSN 0898-1221, Document, MathReview, ZentralBlatt

Referenced by:

§22.20(ii), §22.20(v).

Encodings:

BibTeX

… ►

Elliptic Functions. A Constructive Approach. John Wiley & Sons Ltd., Chichester-New York.

ⓘ

External Links:

ISBN 0-471-96531-6, MathReview (Glenn Stevens), ZentralBlatt

Referenced by:

§20.11(i), §20.4(i), §20.5(i), §20.5(iii), §20.6, §20.7(iv), §20.9(i), §20.9(ii), §20.9(ii), Ch.20, §22.1, §22.11, §22.12, §22.13(i), §22.16(i), §22.2, §22.20(ii), Figure 22.3.2, Figure 22.3.2, §22.4(i), §22.4(ii), §22.6(i), §22.6(iv), §22.7(i), §22.7(ii), §22.8(i), Ch.22, §23.1, §23.10(ii), §23.15(i), §23.17(i), §23.18, §23.2(i), §23.21(ii), §23.3(i), §23.3(ii), §23.5(i), §23.5(ii), §23.5(iii), §23.5(iv), §23.5(v), §23.6(i), §23.8(ii), Ch.23, §4.21(iii), Profile Peter L. Walker.

Encodings:

BibTeX

►

The analyticity of Jacobian functions with respect to the parameter $k$ . Proc. Roy. Soc. London Ser A 459, pp. 2569–2574.

ⓘ

External Links:

ISSN 1364-5021, Document, MathReview, ZentralBlatt

Referenced by:

§22.17(ii), §22.2.

Encodings:

BibTeX

… ►

The distribution of the zeros of Jacobian elliptic functions with respect to the parameter $k$ . Comput. Methods Funct. Theory 9 (2), pp. 579–591.

ⓘ

External Links:

ISSN 1617-9447, MathReview (M. K. Jain), ZentralBlatt

Referenced by:

§22.4(i).

Encodings:

BibTeX

… ►

Elliptic Functions According to Eisenstein and Kronecker. Classics in Mathematics, Springer-Verlag, Berlin.

ⓘ

Notes:

Reprint of the 1976 original

External Links:

ISBN 3-540-65036-9, MathReview, ZentralBlatt

Referenced by:

§22.12, §23.8(ii).

Encodings:

BibTeX

…

17: Bibliography T

… ►

Some definite integrals and Fourier series for Jacobian elliptic functions. Z. Angew. Math. Mech. 49, pp. 95–96.

ⓘ

External Links:

ISSN 0044-2267, Document, MathReview (B. C. Carlson), ZentralBlatt

Referenced by:

§22.11.

Encodings:

BibTeX

… ►

Asymptotic inversion of incomplete gamma functions. Math. Comp. 58 (198), pp. 755–764.

ⓘ

External Links:

ISSN 0025-5718, FullText, Document, MathReview (F. W. J. Olver), ZentralBlatt

Referenced by:

§8.12, §8.12.

Encodings:

BibTeX

►

Asymptotic inversion of the incomplete beta function. J. Comput. Appl. Math. 41 (1-2), pp. 145–157.

ⓘ

Notes:

Asymptotic methods in analysis and combinatorics

External Links:

ISSN 0377-0427, Document, MathReview (Dumitru Acu), ZentralBlatt

Referenced by:

§8.18(ii).

Encodings:

BibTeX

… ►

Algorithm 165: Complete elliptic integrals. Comm. ACM 6 (4), pp. 163–164.

ⓘ

Notes:

Includes Algol program, maximum accuracy 10D. For certification see same journal 6 (1963), pp. 166–167

External Links:

ISSN 0001-0782, Document

Referenced by:

§19.39(ii).

Encodings:

BibTeX

… ►

Eigenfrequencies of an elliptic membrane. Math. Comp. 27 (124), pp. 755–765.

ⓘ

External Links:

FullText, Document, MathReview (Radu Badescu), ZentralBlatt

Referenced by:

4th item.

Encodings:

BibTeX

…