§23.5 Special Lattices

Referenced by:: ¶ ‣ §23.1
Permalink:: http://dlmf.nist.gov/23.5

§23.5(i) Real-Valued Functions
§23.5(ii) Rectangular Lattice
§23.5(iii) Lemniscatic Lattice
§23.5(iv) Rhombic Lattice
§23.5(v) Equianharmonic Lattice

§23.5(i) Real-Valued Functions

Notes:: See Walker (1996, §§7.5, 8.4.2).
Referenced by:: ¶ ‣ §23.6(iv)
Permalink:: http://dlmf.nist.gov/23.5.i

The Weierstrass functions take real values on the real axis iff the lattice is fixed under complex conjugation: $\mathbb{L}=\overline{\mathbb{L}}$ ; equivalently, when $g_{2},g_{3}\in\Real$ . This happens in the cases treated in the following four subsections.

§23.5(ii) Rectangular Lattice

Notes:: See Walker (1996, §8.4.2).
Keywords:: Weierstrass elliptic functions, lattice
Referenced by:: ¶ ‣ §23.6(iv)
Permalink:: http://dlmf.nist.gov/23.5.ii

This occurs when both $\omega _{1}$ and $\omega _{3}/i$ are real and positive. Then $\Delta>0$ and the parallelogram with vertices at 0, $2\omega _{1}$ , $2\omega _{1}+2\omega _{3}$ , $2\omega _{3}$ is a rectangle.

In this case the lattice roots $e_{1}$ , $e_{2}$ , and $e_{3}$ are real and distinct. When they are identified as in (23.3.9)

23.5.1

$e_{1}>e_{2}>e_{3},$

$e_{1}>0>e_{3}.$

Symbols:: $e_{j}$ : zeros
Referenced by:: ¶ ‣ §23.22(ii)
Permalink:: http://dlmf.nist.gov/23.5.E1
Encodings:: TeX, TeX, pMML, pMML, png, png

Also, $e_{2}$ and $g_{3}$ have opposite signs unless $\omega _{3}=i\omega _{1}$ , in which event both are zero.

As functions of $\imagpart{\omega _{3}}$ , $e_{1}$ and $e_{2}$ are decreasing and $e_{3}$ is increasing.

§23.5(iii) Lemniscatic Lattice

Notes:: See Walker (1996, §7.5). Some errors are corrected here.
Keywords:: Weierstrass elliptic functions, lattice
Referenced by:: §22.5(ii)
Permalink:: http://dlmf.nist.gov/23.5.iii

This occurs when $\omega _{1}$ is real and positive and $\omega _{3}=i\omega _{1}$ . The parallelogram 0, $2\omega _{1}$ , $2\omega _{1}+2\omega _{3}$ , $2\omega _{3}$ is a square, and

23.5.2 $\eta _{1}=i\eta _{3}=\pi/(4\omega _{1}),$

Symbols:: $\omega _{1}$ , $\omega _{3}$ , $\omega _{2}=-\omega _{1}-\omega _{3}$ : lattice generators and $\eta _{j}$
Permalink:: http://dlmf.nist.gov/23.5.E2
Encodings:: TeX, pMML, png

23.5.3

$e_{1}=-e_{3}=\left(\mathop{\Gamma\/}\nolimits\!\left(\tfrac{1}{4}\right)\right)^{4}/(32\pi\omega _{1}^{2}),$

$e_{2}=0,$

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, $e_{j}$ : zeros and $\omega _{1}$ , $\omega _{3}$ , $\omega _{2}=-\omega _{1}-\omega _{3}$ : lattice generators
Referenced by:: §23.22(ii)
Permalink:: http://dlmf.nist.gov/23.5.E3
Encodings:: TeX, TeX, pMML, pMML, png, png

23.5.4

$g_{2}=\left(\mathop{\Gamma\/}\nolimits\!\left(\tfrac{1}{4}\right)\right)^{8}/(256\pi^{2}\omega _{1}^{4}),$

$g_{3}=0.$

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, $g_{2}$ , $g_{3}$ : lattice invariants and $\omega _{1}$ , $\omega _{3}$ , $\omega _{2}=-\omega _{1}-\omega _{3}$ : lattice generators
Permalink:: http://dlmf.nist.gov/23.5.E4
Encodings:: TeX, TeX, pMML, pMML, png, png

Note also that in this case $\tau=i$ . In consequence,

23.5.5

$k^{2}=\tfrac{1}{2},$

$\mathop{K\/}\nolimits\!\left(k\right)={\mathop{K\/}\nolimits^{{\prime}}}\!\left(k\right)=\ifrac{\left(\mathop{\Gamma\/}\nolimits\!\left(\tfrac{1}{4}\right)\right)^{2}}{\left(4\sqrt{\pi}\right)}.$

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, $\mathop{K\/}\nolimits\!\left(k\right)$ : Legendre’s complete elliptic integral of the first kind and $k$ : modulus
Permalink:: http://dlmf.nist.gov/23.5.E5
Encodings:: TeX, TeX, pMML, pMML, png, png

§23.5(iv) Rhombic Lattice

Notes:: See Walker (1996, §8.4.2).
Keywords:: Weierstrass elliptic functions, lattice
Permalink:: http://dlmf.nist.gov/23.5.iv

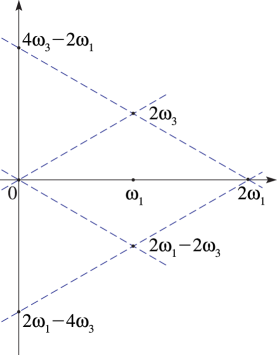
This occurs when $\omega _{1}$ is real and positive, $\imagpart{\omega _{3}}>0$ , $\realpart{\omega _{3}}=\tfrac{1}{2}\omega _{1}$ , and $\Delta<0$ . The parallelogram 0, $2\omega _{1}-2\omega _{3}$ , $2\omega _{1}$ , $2\omega _{3}$ , is a rhombus: see Figure 23.5.1.

The lattice root $e_{1}$ is real, and $e_{3}=\bar{e}_{2}$ , with $\imagpart{e_{2}}>0$ . $e_{1}$ and $g_{3}$ have the same sign unless $2\omega _{3}=(1+i)\omega _{1}$ when both are zero: the pseudo-lemniscatic case. As a function of $\imagpart{e_{3}}$ the root $e_{1}$ is increasing. For the case $\omega _{3}=e^{{\pi i/3}}\omega _{1}$ see §23.5(v).

§23.5(v) Equianharmonic Lattice

Notes:: See Walker (1996, §7.5).
Keywords:: Weierstrass elliptic functions, lattice
Referenced by:: §22.5(ii), §23.5(iv)
Permalink:: http://dlmf.nist.gov/23.5.v

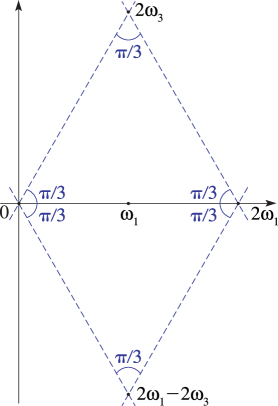
This occurs when $\omega _{1}$ is real and positive and $\omega _{3}=e^{{\pi i/3}}\omega _{1}$ . The rhombus 0, $2\omega _{1}-2\omega _{3}$ , $2\omega _{1}$ , $2\omega _{3}$ can be regarded as the union of two equilateral triangles: see Figure 23.5.2.

Figure 23.5.1: Rhombic lattice. $\realpart{(2\omega _{3})}=\omega _{1}$ .

Symbols:: $\realpart{}$ : real part and $\omega _{1}$ , $\omega _{3}$ , $\omega _{2}=-\omega _{1}-\omega _{3}$ : lattice generators
Referenced by:: §23.5(iv)
Permalink:: http://dlmf.nist.gov/23.5.F1
Encodings:: pdf, png

Figure 23.5.2: Equianharmonic lattice. $2\omega _{3}=e^{{\pi i/3}}2\omega _{1}$ , $2\omega _{1}-2\omega _{3}=e^{{-\pi i/3}}2\omega _{1}$ .

Symbols:: $e$ : base of exponential function and $\omega _{1}$ , $\omega _{3}$ , $\omega _{2}=-\omega _{1}-\omega _{3}$ : lattice generators
Referenced by:: §23.5(v)
Permalink:: http://dlmf.nist.gov/23.5.F2
Encodings:: pdf, png

23.5.6 $\eta _{1}=e^{{\pi i/3}}\eta _{3}=\frac{\pi}{2\sqrt{3}\omega _{1}},$

Symbols:: $e$ : base of exponential function, $\omega _{1}$ , $\omega _{3}$ , $\omega _{2}=-\omega _{1}-\omega _{3}$ : lattice generators and $\eta _{j}$
Permalink:: http://dlmf.nist.gov/23.5.E6
Encodings:: TeX, pMML, png

and the lattice roots and invariants are given by

23.5.7 $e_{1}=e^{{2\pi i/3}}e_{3}=e^{{-2\pi i/3}}e_{2}=\frac{\left(\mathop{\Gamma\/}\nolimits\!\left(\tfrac{1}{3}\right)\right)^{6}}{2^{{14/3}}\pi^{2}\omega _{1}^{2}},$

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, $e$ : base of exponential function, $e_{j}$ : zeros and $\omega _{1}$ , $\omega _{3}$ , $\omega _{2}=-\omega _{1}-\omega _{3}$ : lattice generators
Referenced by:: §23.22(ii)
Permalink:: http://dlmf.nist.gov/23.5.E7
Encodings:: TeX, pMML, png

23.5.8

$g_{2}=0,$

$g_{3}=\frac{\left(\mathop{\Gamma\/}\nolimits\!\left(\tfrac{1}{3}\right)\right)^{{18}}}{(4\pi\omega _{1})^{6}}.$

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, $g_{2}$ , $g_{3}$ : lattice invariants and $\omega _{1}$ , $\omega _{3}$ , $\omega _{2}=-\omega _{1}-\omega _{3}$ : lattice generators
Permalink:: http://dlmf.nist.gov/23.5.E8
Encodings:: TeX, TeX, pMML, pMML, png, png

Note also that in this case $\tau=e^{{i\pi/3}}$ . In consequence,

23.5.9

$k^{2}=e^{{i\pi/3}},$

$\mathop{K\/}\nolimits\!\left(k\right)=e^{{i\pi/6}}{\mathop{K\/}\nolimits^{{\prime}}}\!\left(k\right)=e^{{i\pi/12}}\frac{3^{{1/4}}\left(\mathop{\Gamma\/}\nolimits\!\left(\frac{1}{3}\right)\right)^{3}}{2^{{7/3}}\pi}.$

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, $\mathop{K\/}\nolimits\!\left(k\right)$ : Legendre’s complete elliptic integral of the first kind, $e$ : base of exponential function and $k$ : modulus
Permalink:: http://dlmf.nist.gov/23.5.E9
Encodings:: TeX, TeX, pMML, pMML, png, png