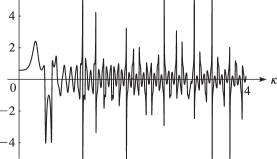22 Jacobian Elliptic Functions Properties 22.2 Definitions 22.4 Periods, Poles, and Zeros

§22.3 Graphics

Permalink:: http://dlmf.nist.gov/22.3

§22.3(i) Real Variables: Line Graphs
§22.3(ii) Real Variables: Surfaces
§22.3(iii) Complex ; Real
§22.3(iv) Complex

§22.3(i) Real Variables: Line Graphs

Notes:: Figures 22.3.1–22.3.12 were produced at NIST and by the authors.
Keywords:: Jacobian elliptic functions
Referenced by:: Figure 22.16.2, Figure 22.16.2, §23.4(i)
Permalink:: http://dlmf.nist.gov/22.3.i

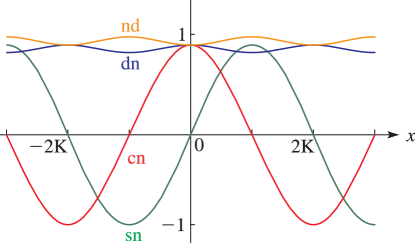
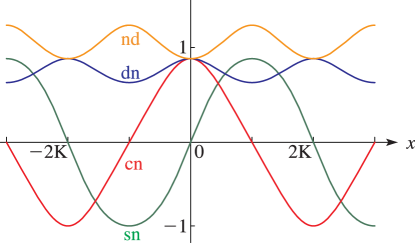
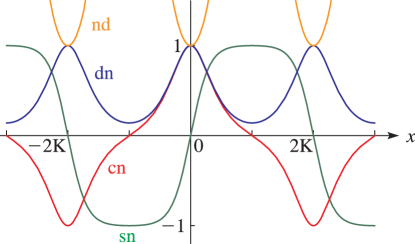
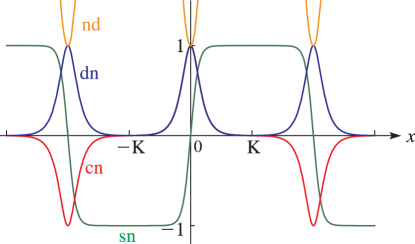
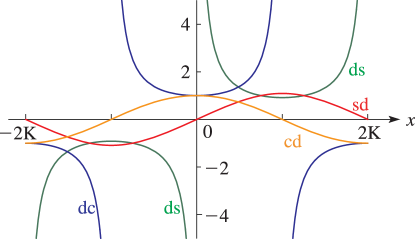
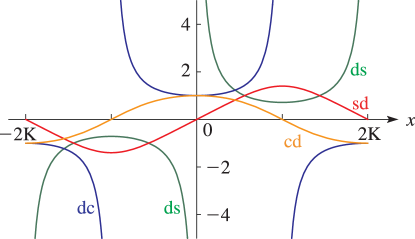
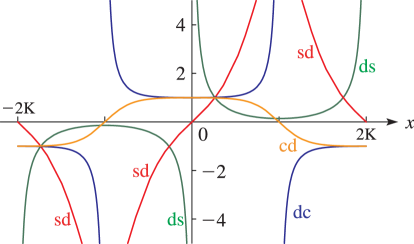
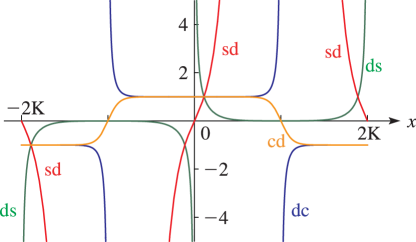
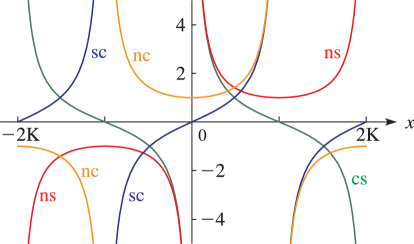
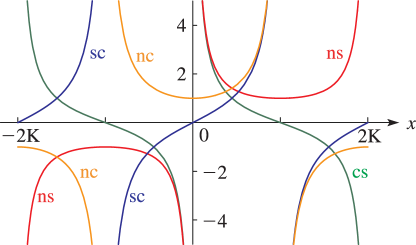
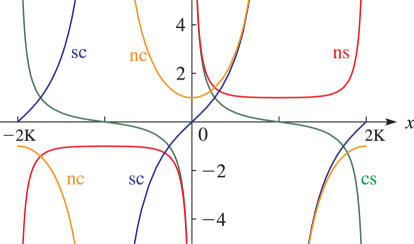
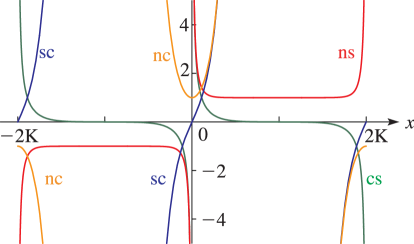
Line graphs of the functions $\mathop{\mathrm{sn}\/}\nolimits\left(x,k\right)$ , $\mathop{\mathrm{cn}\/}\nolimits\left(x,k\right)$ , $\mathop{\mathrm{dn}\/}\nolimits\left(x,k\right)$ , $\mathop{\mathrm{cd}\/}\nolimits\left(x,k\right)$ , $\mathop{\mathrm{sd}\/}\nolimits\left(x,k\right)$ , $\mathop{\mathrm{nd}\/}\nolimits\left(x,k\right)$ , $\mathop{\mathrm{dc}\/}\nolimits\left(x,k\right)$ , $\mathop{\mathrm{nc}\/}\nolimits\left(x,k\right)$ , $\mathop{\mathrm{sc}\/}\nolimits\left(x,k\right)$ , $\mathop{\mathrm{ns}\/}\nolimits\left(x,k\right)$ , $\mathop{\mathrm{ds}\/}\nolimits\left(x,k\right)$ , and $\mathop{\mathrm{cs}\/}\nolimits\left(x,k\right)$ for representative values of real and real illustrating the near trigonometric (), and near hyperbolic () limits.

Figure 22.3.1:

, $-3K\leq x\leq 3K$ , $K=1.6399\dots$ .

Symbols:: $\mathop{K\/}\nolimits\!\left(k\right)$ : Legendre’s complete elliptic integral of the first kind, : real and : modulus
Referenced by:: §22.3(i)
Permalink:: http://dlmf.nist.gov/22.3.F1
Encodings:: pdf, png

Figure 22.3.2:

, $-3K\leq x\leq 3K$ , $K=1.8456\dots$ . For $\mathop{\mathrm{cn}\/}\nolimits\left(x,k\right)$ the curve for $k=1/\sqrt{2}=0.70710\dots$ is a boundary between the curves that have an inflection point in the interval $0\leq x\leq 2\!\mathop{K\/}\nolimits\!\left(k\right)$ , and its translates, and those that do not; see Walker (1996, p. 146).

Symbols:: $\mathop{\mathrm{cn}\/}\nolimits\left(z,k\right)$ : Jacobian elliptic function, $\mathop{K\/}\nolimits\!\left(k\right)$ : Legendre’s complete elliptic integral of the first kind, : real and : modulus
Permalink:: http://dlmf.nist.gov/22.3.F2
Encodings:: pdf, png

Figure 22.3.3:

, $-3K\leq x\leq 3K$ , $K=3.3566\dots$ .

Symbols:: $\mathop{K\/}\nolimits\!\left(k\right)$ : Legendre’s complete elliptic integral of the first kind, : real and : modulus
Permalink:: http://dlmf.nist.gov/22.3.F3
Encodings:: pdf, png

Figure 22.3.4:

, $-3K\leq x\leq 3K$ , $K=7.9474\dots$ .

Symbols:: $\mathop{K\/}\nolimits\!\left(k\right)$ : Legendre’s complete elliptic integral of the first kind, : real and : modulus
Permalink:: http://dlmf.nist.gov/22.3.F4
Encodings:: pdf, png

Figure 22.3.5:

, $-2K\leq x\leq 2K$ , $K=1.6399\dots$ .

Symbols:: $\mathop{K\/}\nolimits\!\left(k\right)$ : Legendre’s complete elliptic integral of the first kind, : real and : modulus
Permalink:: http://dlmf.nist.gov/22.3.F5
Encodings:: pdf, png

Figure 22.3.6:

, $-2K\leq x\leq 2K$ , $K=1.8456\dots$ .

Symbols:: $\mathop{K\/}\nolimits\!\left(k\right)$ : Legendre’s complete elliptic integral of the first kind, : real and : modulus
Permalink:: http://dlmf.nist.gov/22.3.F6
Encodings:: pdf, png

Figure 22.3.7:

, $-2K\leq x\leq 2K$ , $K=3.3566\dots$ .

Symbols:: $\mathop{K\/}\nolimits\!\left(k\right)$ : Legendre’s complete elliptic integral of the first kind, : real and : modulus
Permalink:: http://dlmf.nist.gov/22.3.F7
Encodings:: pdf, png

Figure 22.3.8:

, $-2K\leq x\leq 2K$ , $K=7.9474\dots$ .

Symbols:: $\mathop{K\/}\nolimits\!\left(k\right)$ : Legendre’s complete elliptic integral of the first kind, : real and : modulus
Permalink:: http://dlmf.nist.gov/22.3.F8
Encodings:: pdf, png

Figure 22.3.9:

, $-2K\leq x\leq 2K$ , $K=1.6399\dots$ .

Symbols:: $\mathop{K\/}\nolimits\!\left(k\right)$ : Legendre’s complete elliptic integral of the first kind, : real and : modulus
Permalink:: http://dlmf.nist.gov/22.3.F9
Encodings:: pdf, png

Figure 22.3.10:

, $-2K\leq x\leq 2K$ , $K=1.8456\dots$ .

Symbols:: $\mathop{K\/}\nolimits\!\left(k\right)$ : Legendre’s complete elliptic integral of the first kind, : real and : modulus
Permalink:: http://dlmf.nist.gov/22.3.F10
Encodings:: pdf, png

Figure 22.3.11:

, $-2K\leq x\leq 2K$ , $K=3.3566\dots$ .

Symbols:: $\mathop{K\/}\nolimits\!\left(k\right)$ : Legendre’s complete elliptic integral of the first kind, : real and : modulus
Permalink:: http://dlmf.nist.gov/22.3.F11
Encodings:: pdf, png

Figure 22.3.12:

, $-2K\leq x\leq 2K$ , $K=7.9474\dots$ .

Symbols:: $\mathop{K\/}\nolimits\!\left(k\right)$ : Legendre’s complete elliptic integral of the first kind, : real and : modulus
Referenced by:: §22.3(i)
Permalink:: http://dlmf.nist.gov/22.3.F12
Encodings:: pdf, png

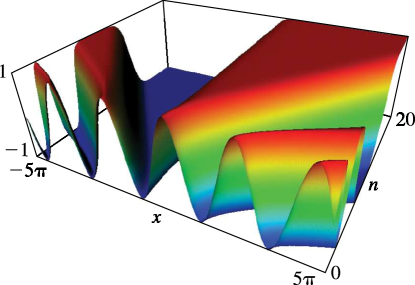
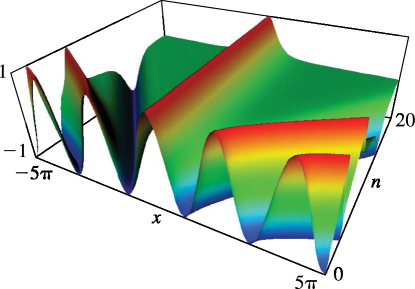
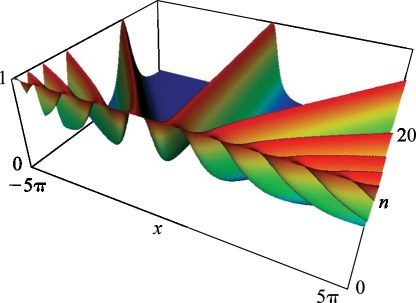
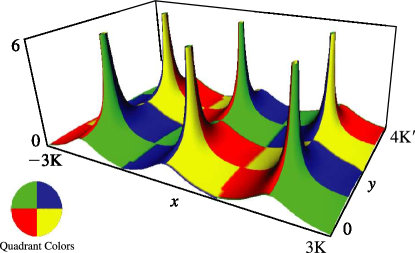
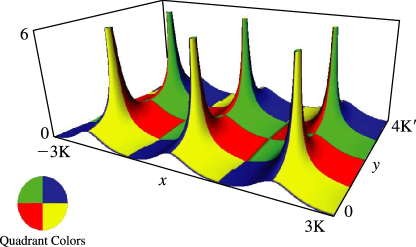
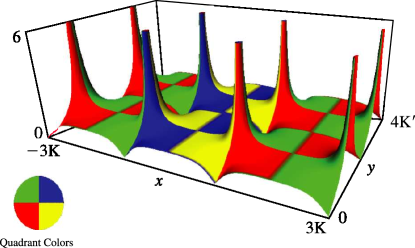
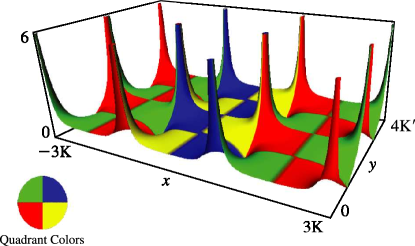
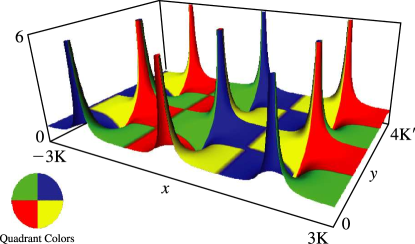
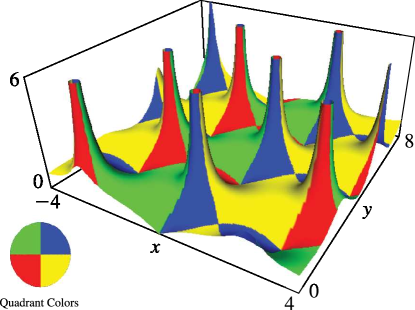
§22.3(ii) Real Variables: Surfaces

Notes:: These graphics were produced at NIST.
Keywords:: Jacobian elliptic functions
Permalink:: http://dlmf.nist.gov/22.3.ii

$\mathop{\mathrm{sn}\/}\nolimits\left(x,k\right)$ , $\mathop{\mathrm{cn}\/}\nolimits\left(x,k\right)$ , and $\mathop{\mathrm{dn}\/}\nolimits\left(x,k\right)$ as functions of real arguments and . The period diverges logarithmically as $k\to 1-$ ; see §19.12.

Visualization Help

Figure 22.3.13: $\mathop{\mathrm{sn}\/}\nolimits\left(x,k\right)$ for $k=1-e^{{-n}}$ ,

to 20, $-5\pi\leq x\leq 5\pi$ .

Symbols:: $\mathop{\mathrm{sn}\/}\nolimits\left(z,k\right)$ : Jacobian elliptic function, : base of exponential function, : real, : modulus and : integer
Permalink:: http://dlmf.nist.gov/22.3.F13
Encodings:: VRML, X3D, pdf, png

Visualization Help

Figure 22.3.14: $\mathop{\mathrm{cn}\/}\nolimits\left(x,k\right)$ for $k=1-e^{{-n}}$ ,

to 20, $-5\pi\leq x\leq 5\pi$ .

Symbols:: $\mathop{\mathrm{cn}\/}\nolimits\left(z,k\right)$ : Jacobian elliptic function, : base of exponential function, : real, : modulus and : integer
Permalink:: http://dlmf.nist.gov/22.3.F14
Encodings:: VRML, X3D, pdf, png

Visualization Help

Figure 22.3.15: $\mathop{\mathrm{dn}\/}\nolimits\left(x,k\right)$ for $k=1-e^{{-n}}$ ,

to 20, $-5\pi\leq x\leq 5\pi$ .

Symbols:: $\mathop{\mathrm{dn}\/}\nolimits\left(z,k\right)$ : Jacobian elliptic function, : base of exponential function, : real, : modulus and : integer
Permalink:: http://dlmf.nist.gov/22.3.F15
Encodings:: VRML, X3D, pdf, png

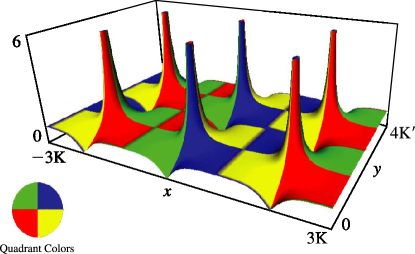
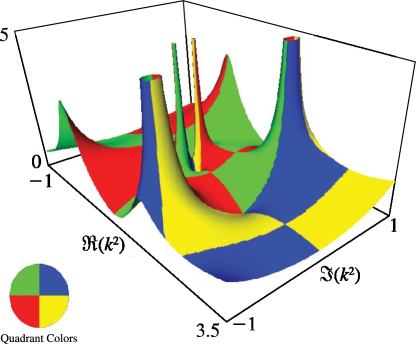
§22.3(iii) Complex ; Real

Notes:: These graphics were produced at NIST and by the authors.
Keywords:: Jacobian elliptic functions
Referenced by:: §23.4(ii)
Permalink:: http://dlmf.nist.gov/22.3.iii

In the graphics shown in this subsection height corresponds to the absolute value of the function and color to the phase. See About Color Map.

Visualization Help

Figure 22.3.16: $\mathop{\mathrm{sn}\/}\nolimits\left(x+iy,k\right)$ for

, $-3K\leq x\leq 3K$ , $0\leq y\leq 4K^{{\prime}}$ . $K=3.3566\dots$ , $K^{{\prime}}=1.5786\dots$ .

Symbols:: $\mathop{\mathrm{sn}\/}\nolimits\left(z,k\right)$ : Jacobian elliptic function, $\mathop{{K^{{\prime}}}\/}\nolimits\!\left(k\right)$ : Legendre’s complementary complete elliptic integral of the first kind, $\mathop{K\/}\nolimits\!\left(k\right)$ : Legendre’s complete elliptic integral of the first kind, : real, : real and : modulus
Permalink:: http://dlmf.nist.gov/22.3.F16
Encodings:: VRML, X3D, pdf, png

Visualization Help

Figure 22.3.17: $\mathop{\mathrm{cn}\/}\nolimits\left(x+iy,k\right)$ for

, $-3K\leq x\leq 3K$ , $0\leq y\leq 4K^{{\prime}}$ . $K=3.3566\dots$ , $K^{{\prime}}=1.5786\dots$ .

Symbols:: $\mathop{\mathrm{cn}\/}\nolimits\left(z,k\right)$ : Jacobian elliptic function, $\mathop{{K^{{\prime}}}\/}\nolimits\!\left(k\right)$ : Legendre’s complementary complete elliptic integral of the first kind, $\mathop{K\/}\nolimits\!\left(k\right)$ : Legendre’s complete elliptic integral of the first kind, : real, : real and : modulus
Permalink:: http://dlmf.nist.gov/22.3.F17
Encodings:: VRML, X3D, pdf, png

Visualization Help

Figure 22.3.18: $\mathop{\mathrm{dn}\/}\nolimits\left(x+iy,k\right)$ for

, $-3K\leq x\leq 3K$ , $0\leq y\leq 4K^{{\prime}}$ . $K=3.3566\dots$ , $K^{{\prime}}=1.5786\dots$ .

Symbols:: $\mathop{\mathrm{dn}\/}\nolimits\left(z,k\right)$ : Jacobian elliptic function, $\mathop{{K^{{\prime}}}\/}\nolimits\!\left(k\right)$ : Legendre’s complementary complete elliptic integral of the first kind, $\mathop{K\/}\nolimits\!\left(k\right)$ : Legendre’s complete elliptic integral of the first kind, : real, : real and : modulus
Permalink:: http://dlmf.nist.gov/22.3.F18
Encodings:: VRML, X3D, pdf, png

Visualization Help

Figure 22.3.19: $\mathop{\mathrm{cd}\/}\nolimits\left(x+iy,k\right)$ for

, $-3K\leq x\leq 3K$ , $0\leq y\leq 4K^{{\prime}}$ . $K=3.3566\dots$ , $K^{{\prime}}=1.5786\dots$ .

Symbols:: $\mathop{\mathrm{cd}\/}\nolimits\left(z,k\right)$ : Jacobian elliptic function, $\mathop{{K^{{\prime}}}\/}\nolimits\!\left(k\right)$ : Legendre’s complementary complete elliptic integral of the first kind, $\mathop{K\/}\nolimits\!\left(k\right)$ : Legendre’s complete elliptic integral of the first kind, : real, : real and : modulus
Permalink:: http://dlmf.nist.gov/22.3.F19
Encodings:: VRML, X3D, pdf, png

Visualization Help

Figure 22.3.20: $\mathop{\mathrm{dc}\/}\nolimits\left(x+iy,k\right)$ for

, $-3K\leq x\leq 3K$ , $0\leq y\leq 4K^{{\prime}}$ . $K=3.3566\dots$ , $K^{{\prime}}=1.5786\dots$ .

Symbols:: $\mathop{\mathrm{dc}\/}\nolimits\left(z,k\right)$ : Jacobian elliptic function, $\mathop{{K^{{\prime}}}\/}\nolimits\!\left(k\right)$ : Legendre’s complementary complete elliptic integral of the first kind, $\mathop{K\/}\nolimits\!\left(k\right)$ : Legendre’s complete elliptic integral of the first kind, : real, : real and : modulus
Permalink:: http://dlmf.nist.gov/22.3.F20
Encodings:: VRML, X3D, pdf, png

Visualization Help

Figure 22.3.21: $\mathop{\mathrm{ns}\/}\nolimits\left(x+iy,k\right)$ for

, $-3K\leq x\leq 3K$ , $0\leq y\leq 4K^{{\prime}}$ . $K=3.3566\dots$ , $K^{{\prime}}=1.5786\dots$ .

Symbols:: $\mathop{\mathrm{ns}\/}\nolimits\left(z,k\right)$ : Jacobian elliptic function, $\mathop{{K^{{\prime}}}\/}\nolimits\!\left(k\right)$ : Legendre’s complementary complete elliptic integral of the first kind, $\mathop{K\/}\nolimits\!\left(k\right)$ : Legendre’s complete elliptic integral of the first kind, : real, : real and : modulus
Permalink:: http://dlmf.nist.gov/22.3.F21
Encodings:: VRML, X3D, pdf, png

§22.3(iv) Complex

Notes:: Figures 22.3.22–22.3.23 and the graphics 22.3.24–22.3.25 were produced at NIST and by the authors. Figures 22.3.26–22.3.29 were produced by the authors.
Keywords:: Jacobian elliptic functions
Referenced by:: §22.1
Permalink:: http://dlmf.nist.gov/22.3.iv

Figure 22.3.22: $\realpart{\mathop{\mathrm{sn}\/}\nolimits\left(x,k\right)}$ ,

, as a function of $k^{2}=i\kappa^{2}$ , $0\leq\kappa\leq 4$ .

Symbols:: $\mathop{\mathrm{sn}\/}\nolimits\left(z,k\right)$ : Jacobian elliptic function, $\realpart{}$ : real part, : real and : modulus
Referenced by:: §22.3(iv), Figures 22.3.22 and 22.3.23, Figures 22.3.22 and 22.3.23
Permalink:: http://dlmf.nist.gov/22.3.F22
Encodings:: pdf, png
Errata (effective with 1.0.5):: The caption for this figure has been corrected. Previously it read, in part, “as a function of $k^{2}=i\kappa$ .” Also, the resolution of the graph was improved, resulting in an additional positive maximum and two additional zero crossings near $\kappa=3$ ; previously it appeared as
Reported 2011-10-30 by Paul Abbott

Figure 22.3.23: $\imagpart{\mathop{\mathrm{sn}\/}\nolimits\left(x,k\right)}$ ,

, as a function of $k^{2}=i\kappa^{2}$ , $0\leq\kappa\leq 4$ .

Symbols:: $\mathop{\mathrm{sn}\/}\nolimits\left(z,k\right)$ : Jacobian elliptic function, $\imagpart{}$ : imaginary part, : real and : modulus
Referenced by:: §22.3(iv), Figures 22.3.22 and 22.3.23
Permalink:: http://dlmf.nist.gov/22.3.F23
Encodings:: pdf, png
Errata (effective with 1.0.5):: The caption for this figure has been corrected. Previously it read, in part, “as a function of $k^{2}=i\kappa$ .”
Reported 2011-10-30 by Paul Abbott

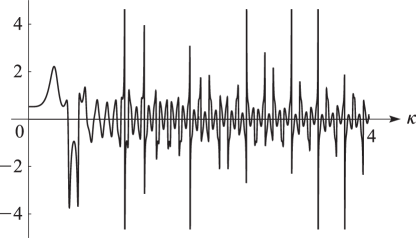
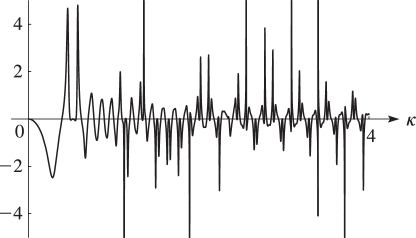
In Figures 22.3.24 and 22.3.25, height corresponds to the absolute value of the function and color to the phase. See p. About Color Map.

Visualization Help

Figure 22.3.24: $\mathop{\mathrm{sn}\/}\nolimits\left(x+iy,k\right)$ for $-4\leq x\leq 4$ , $0\leq y\leq 8$ , $k=1+\tfrac{1}{2}i$ . $K=1.5149\ldots+i0.5235\dots$ , $K^{{\prime}}=1.4620\ldots-i0.3552\dots$ .

Symbols:: $\mathop{\mathrm{sn}\/}\nolimits\left(z,k\right)$ : Jacobian elliptic function, $\mathop{{K^{{\prime}}}\/}\nolimits\!\left(k\right)$ : Legendre’s complementary complete elliptic integral of the first kind, $\mathop{K\/}\nolimits\!\left(k\right)$ : Legendre’s complete elliptic integral of the first kind, : real, : real and : modulus
Keywords:: Jacobian elliptic functions
Referenced by:: §22.3(iv), §22.3(iv), § ‣ DLMF Update; Version 1.0.3
Permalink:: http://dlmf.nist.gov/22.3.F24
Encodings:: VRML, X3D, pdf, png

Visualization Help

Figure 22.3.25: $\mathop{\mathrm{sn}\/}\nolimits\left(5,k\right)$ as a function of complex $k^{2}$ , $-1\leq\realpart{(k^{2})}\leq 3.5$ , $-1\leq\imagpart{(k^{2})}\leq 1$ . Compare §22.17(ii).

Symbols:: $\mathop{\mathrm{sn}\/}\nolimits\left(z,k\right)$ : Jacobian elliptic function, $\imagpart{}$ : imaginary part, $\realpart{}$ : real part and : modulus
Keywords:: Jacobian elliptic functions
Referenced by:: §22.17(ii), §22.3(iv), §22.3(iv)
Permalink:: http://dlmf.nist.gov/22.3.F25
Encodings:: VRML, X3D, pdf, png

Figure 22.3.26: Density plot of $|\mathop{\mathrm{sn}\/}\nolimits\left(5,k\right)|$ as a function of complex $k^{2}$ , $-10\leq\realpart{(k^{2})}\leq 20$ , $-10\leq\imagpart{(k^{2})}\leq 10$ . Grayscale, running from 0 (black) to 10 (white), with $|(\mathop{\mathrm{sn}\/}\nolimits\left(5,k\right))|>10$ truncated to 10. White spots correspond to poles.

Symbols:: $\mathop{\mathrm{sn}\/}\nolimits\left(z,k\right)$ : Jacobian elliptic function, $\imagpart{}$ : imaginary part, $\realpart{}$ : real part and : modulus
Keywords:: Jacobian elliptic functions
Referenced by:: §22.3(iv)
Permalink:: http://dlmf.nist.gov/22.3.F26
Encodings:: pdf, png

Figure 22.3.27: Density plot of $|\mathop{\mathrm{sn}\/}\nolimits\left(10,k\right)|$ as a function of complex $k^{2}$ , $-10\leq\realpart{(k^{2})}\leq 20$ , $-10\leq\imagpart{(k^{2})}\leq 10$ . Grayscale, running from 0 (black) to 10 (white), with $|\mathop{\mathrm{sn}\/}\nolimits\left(10,k\right)|>10$ truncated to 10. White spots correspond to poles.

Symbols:: $\mathop{\mathrm{sn}\/}\nolimits\left(z,k\right)$ : Jacobian elliptic function, $\imagpart{}$ : imaginary part, $\realpart{}$ : real part and : modulus
Keywords:: Jacobian elliptic functions
Permalink:: http://dlmf.nist.gov/22.3.F27
Encodings:: pdf, png

Figure 22.3.28: Density plot of $|\mathop{\mathrm{sn}\/}\nolimits\left(20,k\right)|$ as a function of complex $k^{2}$ , $-10\leq\realpart{(k^{2})}\leq 20$ , $-10\leq\imagpart{(k^{2})}\leq 10$ . Grayscale, running from 0 (black) to 10 (white), with $|\mathop{\mathrm{sn}\/}\nolimits\left(20,k\right)|>10$ truncated to 10. White spots correspond to poles.

Symbols:: $\mathop{\mathrm{sn}\/}\nolimits\left(z,k\right)$ : Jacobian elliptic function, $\imagpart{}$ : imaginary part, $\realpart{}$ : real part and : modulus
Keywords:: Jacobian elliptic functions
Permalink:: http://dlmf.nist.gov/22.3.F28
Encodings:: pdf, png

Figure 22.3.29: Density plot of $|\mathop{\mathrm{sn}\/}\nolimits\left(30,k\right)|$ as a function of complex $k^{2}$ , $-10\leq\realpart{(k^{2})}\leq 20$ , $-10\leq\imagpart{(k^{2})}\leq 10$ . Grayscale, running from 0 (black) to 10 (white), with $|\mathop{\mathrm{sn}\/}\nolimits\left(30,k\right)|>10$ truncated to 10. White spots correspond to poles.

Symbols:: $\mathop{\mathrm{sn}\/}\nolimits\left(z,k\right)$ : Jacobian elliptic function, $\imagpart{}$ : imaginary part, $\realpart{}$ : real part and : modulus
Keywords:: Jacobian elliptic functions
Referenced by:: §22.17(ii), §22.3(iv)
Permalink:: http://dlmf.nist.gov/22.3.F29
Encodings:: pdf, png

© 2010–2013 NIST / Privacy Policy / Disclaimer / Feedback; Version 1.0.6; Release date 2013-05-06 Math-Image version (See MathML) . A Printed Companionis available. 22.2 Definitions 22.4 Periods, Poles, and Zeros

§22.3 Graphics

Contents

§22.3(i) Real Variables: Line Graphs

§22.3(ii) Real Variables: Surfaces

§22.3(iii) Complex ; Real

§22.3(iv) Complex