§22.4 Periods, Poles, and Zeros
Contents
- §22.4(i) Distribution
- §22.4(ii) Graphical Interpretation via Glaisher’s Notation
- §22.4(iii) Translation by Half or Quarter Periods
§22.4(i) Distribution
For each Jacobian function, Table 22.4.1 gives its periods in the -plane in the left column, and the position of one of its poles in the second row. The other poles are at congruent points, which is the set of points obtained by making translations by , where . For example, the poles of , abbreviated as in the following tables, are at .
| Periods | -Poles | |||
|---|---|---|---|---|
| , | ||||
| , | ||||
| , | ||||
Three functions in the same column of Table 22.4.1 are copolar, and four functions in the same row are coperiodic.
Table 22.4.2 displays the periods and zeros of the functions in the -plane in a similar manner to Table 22.4.1. Again, one member of each congruent set of zeros appears in the second row; all others are generated by translations of the form , where .
| Periods | -Zeros | |||
|---|---|---|---|---|
| , | ||||
| , | ||||
| , | ||||
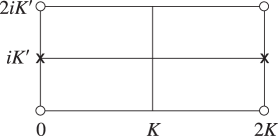
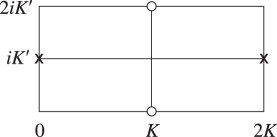
Figure 22.4.1 illustrates the locations in the -plane of the poles and zeros of the three principal Jacobian functions in the rectangle with vertices , , , . The other poles and zeros are at the congruent points.
 |
 |
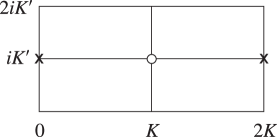 |
| (a) | (b) | (c) |
For the distribution of the -zeros of the Jacobian elliptic functions see Walker (2009).
§22.4(ii) Graphical Interpretation via Glaisher’s Notation
Figure 22.4.2 depicts the fundamental unit cell in the -plane, with vertices , , , . The set of points , , comprise the lattice for the 12 Jacobian functions; all other lattice unit cells are generated by translation of the fundamental unit cell by , where again .

Using the p,q notation of (22.2.10), Figure 22.4.2 serves as a mnemonic for the poles, zeros, periods, and half-periods of the 12 Jacobian elliptic functions as follows. Let p,q be any two distinct letters from the set s,c,d,n which appear in counterclockwise orientation at the corners of all lattice unit cells. Then: (a) In any lattice unit cell has a simple zero at and a simple pole at . (b) The difference between p and the nearest q is a half-period of . This half-period will be plus or minus a member of the triple ; the other two members of this triple are quarter periods of .
§22.4(iii) Translation by Half or Quarter Periods
See Table 22.4.3.
For example, . (The modulus is suppressed throughout the table.)
