DLMF: Untitled Document

… ►

•

Cody (1969) provides minimax rational approximations for $\operatorname{erf}x$ and $\operatorname{erfc}x$ . The maximum relative precision is about 20S.

… ►

•

Cody et al. (1970) gives minimax rational approximations to Dawson’s integral $F\left(x\right)$ (maximum relative precision 20S–22S).

… ►

•

Luke (1969b, pp. 323–324) covers $\frac{1}{2}\sqrt{\pi}\operatorname{erf}x$ and $e^{x^{2}}F\left(x\right)$ for $-3\leq x\leq 3$ (the Chebyshev coefficients are given to 20D); $\sqrt{\pi}xe^{x^{2}}\operatorname{erfc}x$ and $2xF\left(x\right)$ for $x\geq 3$ (the Chebyshev coefficients are given to 20D and 15D, respectively). Coefficients for the Fresnel integrals are given on pp. 328–330 (20D).

… ►

•

Shepherd and Laframboise (1981) gives coefficients of Chebyshev series for $(1+2x)e^{x^{2}}\operatorname{erfc}x$ on $(0,\infty)$ (22D).

… ►

•

Luke (1969b, vol. 2, pp. 422–435) gives main diagonal Padé approximations for $F\left(z\right)$ , $\operatorname{erf}z$ , $\operatorname{erfc}z$ , $C\left(z\right)$ , and $S\left(z\right)$ ; approximate errors are given for a selection of $z$ -values.

… ►

•

Abramowitz and Stegun (1964, Chapter 7) includes $\operatorname{erf}x$ , $(2/\sqrt{\pi})e^{-x^{2}}$ , $x\in[0,2]$ , 10D; $(2/\sqrt{\pi})e^{-x^{2}}$ , $x\in[2,10]$ , 8S; $xe^{x^{2}}\operatorname{erfc}x$ , $x^{-2}\in[0,0.25]$ , 7D; $2^{n}\Gamma\left(\frac{1}{2}n+1\right)\mathop{\mathrm{i}^{n}\mathrm{erfc}}% \left(x\right)$ , $n=1(1)6,10,11$ , $x\in[0,5]$ , 6S; $F\left(x\right)$ , $x\in[0,2]$ , 10D; $xF\left(x\right)$ , $x^{-2}\in[0,0.25]$ , 9D; $C\left(x\right)$ , $S\left(x\right)$ , $x\in[0,5]$ , 7D; $\mathrm{f}\left(x\right)$ , $\mathrm{g}\left(x\right)$ , $x\in[0,1]$ , $x^{-1}\in[0,1]$ , 15D.

►

•

Abramowitz and Stegun (1964, Table 27.6) includes the Goodwin–Staton integral $G\left(x\right)$ , $x=1(.1)3(.5)8$ , 4D; also $G\left(x\right)+\ln x$ , $x=0(.05)1$ , 4D.

… ►

•

Zhang and Jin (1996, pp. 637, 639) includes $(2/\sqrt{\pi})e^{-x^{2}}$ , $\operatorname{erf}x$ , $x=0(.02)1(.04)3$ , 8D; $C\left(x\right)$ , $S\left(x\right)$ , $x=0(.2)10(2)100(100)500$ , 8D.

… ►

•

Zhang and Jin (1996, pp. 638, 640–641) includes the real and imaginary parts of $\operatorname{erf}z$ , $x\in[0,5]$ , $y=0.5(.5)3$ , 7D and 8D, respectively; the real and imaginary parts of $\int_{x}^{\infty}e^{\pm\mathrm{i}t^{2}}\,\mathrm{d}t$ , $(1/\sqrt{\pi})e^{\mp\mathrm{i}(x^{2}+(\pi/4))}\int_{x}^{\infty}e^{\pm\mathrm{i% }t^{2}}\,\mathrm{d}t$ , $x=0(.5)20(1)25$ , 8D, together with the corresponding modulus and phase to 8D and 6D (degrees), respectively.

… ►

•

Fettis et al. (1973) gives the first 100 zeros of $\operatorname{erf}z$ and $w\left(z\right)$ (the table on page 406 of this reference is for $w\left(z\right)$ , not for $\operatorname{erfc}z$ ), 11S.

…

… ►

§6.19(ii) Real Variables

►

•

Abramowitz and Stegun (1964, Chapter 5) includes $x^{-1}\operatorname{Si}\left(x\right)$ , $-x^{-2}\operatorname{Cin}\left(x\right)$ , $x^{-1}\operatorname{Ein}\left(x\right)$ , $-x^{-1}\operatorname{Ein}\left(-x\right)$ , $x=0(.01)0.5$ ; $\operatorname{Si}\left(x\right)$ , $\operatorname{Ci}\left(x\right)$ , $\operatorname{Ei}\left(x\right)$ , $E_{1}\left(x\right)$ , $x=0.5(.01)2$ ; $\operatorname{Si}\left(x\right)$ , $\operatorname{Ci}\left(x\right)$ , $xe^{-x}\operatorname{Ei}\left(x\right)$ , $xe^{x}E_{1}\left(x\right)$ , $x=2(.1)10$ ; $x\mathrm{f}\left(x\right)$ , $x^{2}\mathrm{g}\left(x\right)$ , $xe^{-x}\operatorname{Ei}\left(x\right)$ , $xe^{x}E_{1}\left(x\right)$ , $x^{-1}=0(.005)0.1$ ; $\operatorname{Si}\left(\pi x\right)$ , $\operatorname{Cin}\left(\pi x\right)$ , $x=0(.1)10$ . Accuracy varies but is within the range 8S–11S.

►

•

Zhang and Jin (1996, pp. 652, 689) includes $\operatorname{Si}\left(x\right)$ , $\operatorname{Ci}\left(x\right)$ , $x=0(.5)20(2)30$ , 8D; $\operatorname{Ei}\left(x\right)$ , $E_{1}\left(x\right)$ , $x=[0,100]$ , 8S.

… ►

•

Abramowitz and Stegun (1964, Chapter 5) includes the real and imaginary parts of $ze^{z}E_{1}\left(z\right)$ , $x=-19(1)20$ , $y=0(1)20$ , 6D; $e^{z}E_{1}\left(z\right)$ , $x=-4(.5)-2$ , $y=0(.2)1$ , 6D; $E_{1}\left(z\right)+\ln z$ , $x=-2(.5)2.5$ , $y=0(.2)1$ , 6D.

►

•

Zhang and Jin (1996, pp. 690–692) includes the real and imaginary parts of $E_{1}\left(z\right)$ , $\pm x=0.5,1,3,5,10,15,20,50,100$ , $y=0(.5)1(1)5(5)30,50,100$ , 8S.

… ►

•

Cody and Thacher (1968) provides minimax rational approximations for $E_{1}\left(x\right)$ , with accuracies up to 20S.

►

•

Cody and Thacher (1969) provides minimax rational approximations for $\operatorname{Ei}\left(x\right)$ , with accuracies up to 20S.

… ►

•

Luke (1969b, pp. 41–42) gives Chebyshev expansions of $\operatorname{Ein}\left(ax\right)$ , $\operatorname{Si}\left(ax\right)$ , and $\operatorname{Cin}\left(ax\right)$ for $-1\leq x\leq 1$ , $a\in\mathbb{C}$ . The coefficients are given in terms of series of Bessel functions.

►

•

Luke (1969b, pp. 321–322) covers $\operatorname{Ein}\left(x\right)$ and $-\operatorname{Ein}\left(-x\right)$ for $0\leq x\leq 8$ (the Chebyshev coefficients are given to 20D); $E_{1}\left(x\right)$ for $x\geq 5$ (20D), and $\operatorname{Ei}\left(x\right)$ for $x\geq 8$ (15D). Coefficients for the sine and cosine integrals are given on pp. 325–327.

… ►

•

Luke (1969b, pp. 411–414) gives rational approximations for $\operatorname{Ein}\left(z\right)$ .

… ►

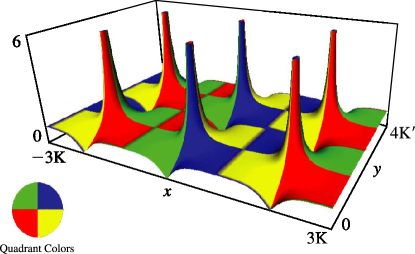
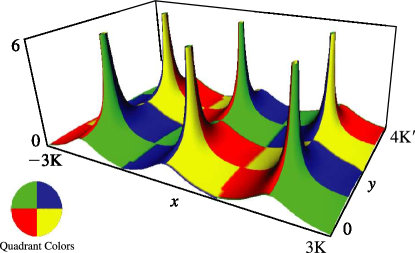
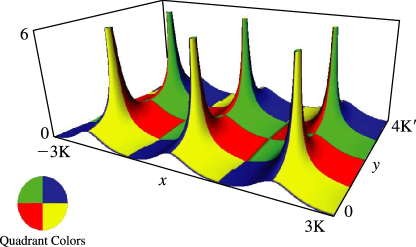
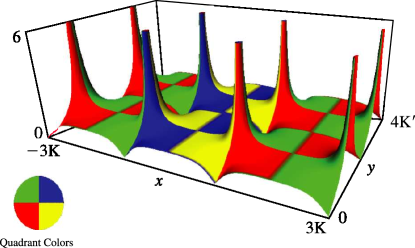
See accompanying text — Figure 22.3.16: $\operatorname{sn}\left(x+iy,k\right)$ for $k=0.99$ , $-3K\leq x\leq 3K$ , $0\leq y\leq 4K^{\prime}$ . $K=3.3566\dots$ , $K^{\prime}=1.5786\dots$ . Magnify 3D Help

►

…

… ►

FDLIBM (free C library)

ⓘ

Notes:: The “Freely Distributable LIBM” package provides implementations of standard elementary functions plus a few higher functions, e.g. gamma. Double precision, maximum accuracy 20S. Developed by Sun Microsystems.
External Links:: GAMS (package FDLIBM)
Referenced by:: § ‣ Software Cross Index, § ‣ Software Cross Index.
Encodings:: BibTeX

… ►

S. Fempl (1960) Sur certaines sommes des intégral-cosinus. Bull. Soc. Math. Phys. Serbie 12, pp. 13–20 (French).

ⓘ

External Links:: MathReview (L. Carlitz), ZentralBlatt
Referenced by:: §6.15.
Encodings:: BibTeX

… ►

H. E. Fettis, J. C. Caslin, and K. R. Cramer (1973) Complex zeros of the error function and of the complementary error function. Math. Comp. 27 (122), pp. 401–407.

ⓘ

External Links:: FullText, MathReview, ZentralBlatt
Referenced by:: §7.13(i), §7.13(ii), 1st item.
Encodings:: BibTeX

►

H. E. Fettis and J. C. Caslin (1964) Tables of Elliptic Integrals of the First, Second, and Third Kind. Technical report Technical Report ARL 64-232, Aerospace Research Laboratories, Wright-Patterson Air Force Base, Ohio.

ⓘ

Notes:: Reviewed in Math. Comp. v. 1919(1965)509. Table erratum: Math. Comp. v. 20 (1966), no. 96, pp. 639-640.
Referenced by:: §19.37(ii), §19.37(ii), §19.37(iii), §19.37(iii), §19.37(iii).
Encodings:: BibTeX

… ►

G. Freud (1969) On weighted polynomial approximation on the whole real axis. Acta Math. Acad. Sci. Hungar. 20, pp. 223–225.

ⓘ

External Links:: ISSN 0001-5954, Document, Link, MathReview (A. K. Varma)
Referenced by:: §18.32.
Encodings:: BibTeX

…

§7.8 Inequalities

… ►

7.8.6

\int_{0}^{x}e^{at^{2}}\,\mathrm{d}t<\frac{1}{3ax}\left(2e^{ax^{2}}+ax^{2}-2% \right),

a,x>0

.

ⓘ

Symbols:: $\,\mathrm{d}\NVar{x}$ : differential of $x$ , $\mathrm{e}$ : base of natural logarithm, $\int$ : integral and $x$ : real variable
Referenced by:: §7.8
Permalink:: http://dlmf.nist.gov/7.8.E6
Encodings:: pMML, png, TeX
See also:: Annotations for §7.8 and Ch.7

►

7.8.7

\frac{\sinh x^{2}}{x}<{\mathrm{e}}^{x^{2}}F\left(x\right)=\int_{0}^{x}{\mathrm% {e}}^{t^{2}}\,\mathrm{d}t<\frac{{\mathrm{e}}^{x^{2}}-1}{x},

x>0

.

ⓘ

Symbols:: $F\left(\NVar{z}\right)$ : Dawson’s integral, $\,\mathrm{d}\NVar{x}$ : differential of $x$ , $\mathrm{e}$ : base of natural logarithm, $\sinh\NVar{z}$ : hyperbolic sine function, $\int$ : integral and $x$ : real variable
Referenced by:: Erratum (V1.1.5) for Additions
Permalink:: http://dlmf.nist.gov/7.8.E7
Encodings:: pMML, png, TeX
Addition (effective with 1.1.5):: A new inequality was added.
See also:: Annotations for §7.8 and Ch.7

►The function

F\left(x\right)/\sqrt{1-{\mathrm{e}}^{-2x^{2}}}

is strictly decreasing for

x>0

. For these and similar results for Dawson’s integral

F\left(x\right)

see Janssen (2021). …

… ► ►►►►►►►

	Open Source												With Book						Commercial
…
6 Exponential, Logarithmic, Sine, and Cosine Integrals
6.21(ii) $E_{1}\left(x\right)$ , $\operatorname{Ei}\left(x\right)$ , $\operatorname{Si}\left(x\right)$ , $\operatorname{Ci}\left(x\right)$ , $\operatorname{Shi}\left(x\right)$ , $\operatorname{Chi}\left(x\right)$ , $x\in\mathbb{R}$	✓	✓	✓	✓	✓	✓	✓		✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓
…
7.25(ii) $\operatorname{erf}x$ , $\operatorname{erfc}x$ , $\mathop{\mathrm{i}^{n}\mathrm{erfc}}\left(x\right)$ , $x\in\mathbb{R}$	✓		✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓		✓	✓	✓	✓	✓	✓	NMS
…
8.28(vii) $E_{p}\left(z\right)$ , $z,p\in\mathbb{C}$	✓										✓	✓								✓	✓	✓
…
20 Theta Functions
…

…

… ►

Subsection 19.2(ii) and Equation (19.2.9)

The material surrounding (19.2.8), (19.2.9) has been updated so that the complementary complete elliptic integrals of the first and second kind are defined with consistent multivalued properties and correct analytic continuation. In particular, (19.2.9) has been corrected to read

19.2.9

{K^{\prime}}\left(k\right)=\begin{cases}K\left(k^{\prime}\right),&|% \operatorname{ph}k|\leq\tfrac{1}{2}\pi,\\ K\left(k^{\prime}\right)\mp 2\mathrm{i}K\left(-k\right),&\tfrac{1}{2}\pi<\pm% \operatorname{ph}k<\pi,\end{cases}

{E^{\prime}}\left(k\right)=\begin{cases}E\left(k^{\prime}\right),&|% \operatorname{ph}k|\leq\tfrac{1}{2}\pi,\\ E\left(k^{\prime}\right)\mp 2\mathrm{i}(K\left(-k\right)-E\left(-k\right)),&% \tfrac{1}{2}\pi<\pm\operatorname{ph}k<\pi\end{cases}

… ►

Equations (22.14.16), (22.14.17)

22.14.16

\int_{0}^{K\left(k\right)}\ln\left(\operatorname{sn}\left(t,k\right)\right)\,% \mathrm{d}t=-\tfrac{\pi}{4}{K^{\prime}}\left(k\right)-\tfrac{1}{2}K\left(k% \right)\ln k,

22.14.17

\int_{0}^{K\left(k\right)}\ln\left(\operatorname{cn}\left(t,k\right)\right)\,% \mathrm{d}t=-\tfrac{\pi}{4}{K^{\prime}}\left(k\right)+\tfrac{1}{2}K\left(k% \right)\ln\left(k^{\prime}/k\right)

Originally, a factor of $\pi$ was missing from the terms containing the $-\tfrac{1}{4}{K^{\prime}}\left(k\right)$ .

Reported by Fred Hucht on 2020-08-06

… ►

Equation (8.12.5)

To be consistent with the notation used in (8.12.16), Equation (8.12.5) was changed to read

8.12.5

\frac{{\mathrm{e}}^{\pm\pi\mathrm{i}a}}{2\mathrm{i}\sin(\pi a)}Q\left(-a,z{% \mathrm{e}}^{\pm\pi\mathrm{i}}\right)=\pm\tfrac{1}{2}\operatorname{erfc}\left(% \pm\mathrm{i}\eta\sqrt{a/2}\right)-\mathrm{i}T(a,\eta)

… ►

Chapters 8, 20, 36

Several new equations have been added. See (8.17.24), (20.7.34), §20.11(v), (26.12.27), (36.2.28), and (36.2.29).

… ►

References

Bibliographic citations were added in §§1.13(v), 10.14, 10.21(ii), 18.15(v), 18.32, 30.16(iii), 32.13(ii), and as general references in Chapters 19, 20, 22, and 23.

…

… ►

C. Chiccoli, S. Lorenzutta, and G. Maino (1987) A numerical method for generalized exponential integrals. Comput. Math. Appl. 14 (4), pp. 261–268.

ⓘ

External Links:: ISSN 0898-1221, MathReview (R. P. Boas), ZentralBlatt
Referenced by:: §8.25(v).
Encodings:: BibTeX

►

C. Chiccoli, S. Lorenzutta, and G. Maino (1988) On the evaluation of generalized exponential integrals

{E}_{v}(x)

. J. Comput. Phys. 78 (2), pp. 278–287.

ⓘ

External Links:: ISSN 0021-9991, Document, MathReview, ZentralBlatt
Referenced by:: §8.25(v), 2nd item.
Encodings:: BibTeX

►

C. Chiccoli, S. Lorenzutta, and G. Maino (1990a) An algorithm for exponential integrals of real order. Computing 45 (3), pp. 269–276.

ⓘ

Notes:: Includes Fortran code
External Links:: ISSN 0010-485X, Document, MathReview, ZentralBlatt
Referenced by:: §8.25(v), §8.28(vi).
Encodings:: BibTeX

►

C. Chiccoli, S. Lorenzutta, and G. Maino (1990b) On a Tricomi series representation for the generalized exponential integral. Internat. J. Comput. Math. 31, pp. 257–262.

ⓘ

Notes:: Includes Fortran code
External Links:: Document, ZentralBlatt
Referenced by:: §8.28(vi).
Encodings:: BibTeX

… ►

M. S. Corrington (1961) Applications of the complex exponential integral. Math. Comp. 15 (73), pp. 1–6.

ⓘ

External Links:: FullText, MathReview (J. C. P. Miller), ZentralBlatt
Referenced by:: §6.7(iv).
Encodings:: BibTeX

…

complementary%20exponential%20integral

1—10 of 11 matching pages

1: 7.24 Approximations

2: 7.23 Tables

3: 6.19 Tables

§6.19(ii) Real Variables

4: 6.20 Approximations

5: 22.3 Graphics

6: Bibliography F

7: 7.8 Inequalities

§7.8 Inequalities

8: Software Index

9: Errata

10: Bibliography C