§5.12 Beta Function
In this section all fractional powers have their principal values, except where noted otherwise. In (5.12.1)–(5.12.4) it is assumed and .
Euler’s Beta Integral
| 5.12.1 | |||
| 5.12.2 | |||
| 5.12.3 | |||
| 5.12.4 | |||
| . | |||
| 5.12.5 | |||
| . | |||
| 5.12.6 | |||
| . | |||
| 5.12.7 | |||
| . | |||
| 5.12.8 | |||
| , , . | |||
In (5.12.8) the fractional powers have their principal values when and , and are continued via continuity.
| 5.12.9 | |||
| , . | |||
| 5.12.10 | |||
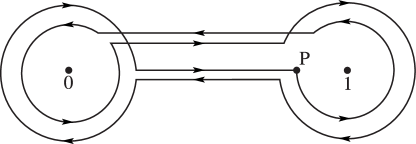
| , | |||
with the contour as shown in Figure 5.12.1.
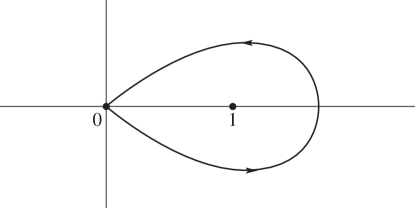
In (5.12.11) and (5.12.12) the fractional powers are continuous on the integration paths and take their principal values at the beginning.
| 5.12.11 | |||
when , is not an integer and the contour cuts the real axis between and the origin. See Figure 5.12.2.
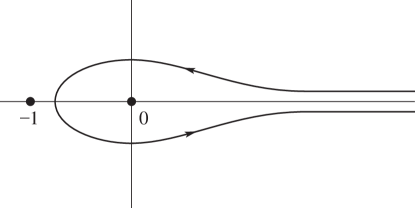
Pochhammer’s Integral
When
| 5.12.12 | |||
where the contour starts from an arbitrary point in the interval , circles and then in the positive sense, circles and then in the negative sense, and returns to . It can always be deformed into the contour shown in Figure 5.12.3.