Pochhammer integral

SearchAdvancedHelp

(0.005 seconds)

1—10 of 51 matching pages

1: 7.12 Asymptotic Expansions

… ►

7.12.2 $$\mathrm{f}\left(z\right)\sim \frac{1}{\pi z}\sum _{m=0}^{\mathrm{\infty }}{(-1)}^m\frac{{\left(\frac{1}{2}\right)}_{2m}}{{(\pi z^2/2)}^{2m}},$$

ⓘ

Symbols:

$\mathrm{f}\left(z\right)$: auxiliary function for Fresnel integrals, ${\left(a\right)}_n$: Pochhammer’s symbol (or shifted factorial), $\sim$: Poincaré asymptotic expansion, $\pi$: the ratio of the circumference of a circle to its diameter and $z$: complex variable

A&S Ref:

7.3.27

Referenced by:

§7.12(ii), §7.12(ii), Erratum (V1.0.9) for Chapters 7, 25

Permalink:

http://dlmf.nist.gov/7.12.E2

Encodings:

pMML, png, TeX

Notational Change (effective with 1.0.9):

Previously the RHS of this equation was written as $\frac{1}{\pi z}{\sum }_{m=0}^{\mathrm{\infty }}{(-1)}^m\frac{1\cdot 3\cdot 5\mathrm{\cdots }(4m-1)}{{(\pi z^2)}^{2m}}$. We have rewritten the sum more concisely using Pochhammer’s symbol.

Suggested 2014-03-13 by Giorgos Karagounis

See also:

Annotations for §7.12(ii), §7.12 and Ch.7

►

7.12.3 $$\mathrm{g}\left(z\right)\sim \frac{1}{\pi z}\sum _{m=0}^{\mathrm{\infty }}{(-1)}^m\frac{{\left(\frac{1}{2}\right)}_{2m+1}}{{(\pi z^2/2)}^{2m+1}},$$

ⓘ

Symbols:

$\mathrm{g}\left(z\right)$: auxiliary function for Fresnel integrals, ${\left(a\right)}_n$: Pochhammer’s symbol (or shifted factorial), $\sim$: Poincaré asymptotic expansion, $\pi$: the ratio of the circumference of a circle to its diameter and $z$: complex variable

A&S Ref:

7.3.28

Referenced by:

§7.12(ii), §7.12(ii), Erratum (V1.0.9) for Chapters 7, 25

Permalink:

http://dlmf.nist.gov/7.12.E3

Encodings:

pMML, png, TeX

Notational Change (effective with 1.0.9):

Previously the RHS of this equation was written as $\frac{1}{{\pi }^2{z}^3}{\sum }_{m=0}^{\mathrm{\infty }}{(-1)}^m\frac{1\cdot 3\cdot 5\mathrm{\cdots }(4m+1)}{{(\pi z^2)}^{2m}}$ We have rewritten the sum more concisely using Pochhammer’s symbol.

Suggested 2014-03-13 by Giorgos Karagounis

See also:

Annotations for §7.12(ii), §7.12 and Ch.7

… ►

7.12.4 $$\mathrm{f}\left(z\right)=\frac{1}{\pi z}\sum _{m=0}^{n-1}{(-1)}^m\frac{{\left(\frac{1}{2}\right)}_{2m}}{{(\pi z^2/2)}^{2m}}+R_n^{(\mathrm{f})}(z),$$

ⓘ

Symbols:

$\mathrm{f}\left(z\right)$: auxiliary function for Fresnel integrals, ${\left(a\right)}_n$: Pochhammer’s symbol (or shifted factorial), $\pi$: the ratio of the circumference of a circle to its diameter, $z$: complex variable, $n$: nonnegative integer and $R_n^{(\mathrm{f})}(z)$: remainder term

A&S Ref:

7.3.27 (in different form)

Referenced by:

§7.12(ii), Erratum (V1.0.9) for Chapters 7, 25

Permalink:

http://dlmf.nist.gov/7.12.E4

Encodings:

pMML, png, TeX

Notational Change (effective with 1.0.9):

Previously the RHS of this equation was written as $\frac{1}{\pi z}{\sum }_{m=0}^{n-1}{(-1)}^m\frac{1\cdot 3\mathrm{\cdots }(4m-1)}{{(\pi z^2)}^{2m}}+R_n^{(\mathrm{f})}(z)$. We have rewritten the sum more concisely using Pochhammer’s symbol.

Suggested 2014-03-13 by Giorgos Karagounis

See also:

Annotations for §7.12(ii), §7.12 and Ch.7

►

7.12.5 $$\mathrm{g}\left(z\right)=\frac{1}{\pi z}\sum _{m=0}^{n-1}{(-1)}^m\frac{{\left(\frac{1}{2}\right)}_{2m+1}}{{(\pi z^2/2)}^{2m+1}},+R_n^{(\mathrm{g})}(z),$$

ⓘ

Symbols:

$\mathrm{g}\left(z\right)$: auxiliary function for Fresnel integrals, ${\left(a\right)}_n$: Pochhammer’s symbol (or shifted factorial), $\pi$: the ratio of the circumference of a circle to its diameter, $z$: complex variable, $n$: nonnegative integer and $R_n^{(\mathrm{g})}(z)$: remainder term

A&S Ref:

7.3.28 (in different form)

Referenced by:

Erratum (V1.0.9) for Chapters 7, 25

Permalink:

http://dlmf.nist.gov/7.12.E5

Encodings:

pMML, png, TeX

Notational Change (effective with 1.0.9):

Previously the RHS of this equation was written as $\frac{1}{{\pi }^2{z}^3}{\sum }_{m=0}^{n-1}{(-1)}^m\frac{1\cdot 3\mathrm{\cdots }(4m+1)}{{(\pi z^2)}^{2m}}+R_n^{(\mathrm{g})}(z)$. We have rewritten the sum more concisely using Pochhammer’s symbol.

Suggested 2014-03-13 by Giorgos Karagounis

See also:

Annotations for §7.12(ii), §7.12 and Ch.7

…

2: 17.13 Integrals

… ►

17.13.1 $${\int }_{-c}^d\frac{{(-qx/c;q)}_{\mathrm{\infty }}{(qx/d;q)}_{\mathrm{\infty }}}{{(-ax/c;q)}_{\mathrm{\infty }}{(bx/d;q)}_{\mathrm{\infty }}}{d}_{q}x=\frac{(1-q){(q;q)}_{\mathrm{\infty }}{(ab;q)}_{\mathrm{\infty }}cd{(-c/d;q)}_{\mathrm{\infty }}{(-d/c;q)}_{\mathrm{\infty }}}{{(a;q)}_{\mathrm{\infty }}{(b;q)}_{\mathrm{\infty }}(c+d){(-bc/d;q)}_{\mathrm{\infty }}{(-ad/c;q)}_{\mathrm{\infty }}},$$

ⓘ

Symbols:

$\int$: integral, ${(a;q)}_n$: $q$-Pochhammer symbol (or $q$-shifted factorial), $d_{q}x$: $q$-differential, $q$: complex base and $x$: real variable

Permalink:

http://dlmf.nist.gov/17.13.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §17.13 and Ch.17

… ►

17.13.2 $${\int }_{-c}^d\frac{{(-qx/c;q)}_{\mathrm{\infty }}{(qx/d;q)}_{\mathrm{\infty }}}{{(-x{q}^{\alpha }/c;q)}_{\mathrm{\infty }}{(x{q}^{\beta }/d;q)}_{\mathrm{\infty }}}{d}_{q}x=\frac{{\mathrm{\Gamma }}_q\left(\alpha \right){\mathrm{\Gamma }}_q\left(\beta \right)}{{\mathrm{\Gamma }}_q\left(\alpha +\beta \right)}\frac{cd}{c+d}\frac{{(-c/d;q)}_{\mathrm{\infty }}{(-d/c;q)}_{\mathrm{\infty }}}{{(-q^{\beta }c/d;q)}_{\mathrm{\infty }}{(-q^{\alpha }d/c;q)}_{\mathrm{\infty }}}.$$

ⓘ

Symbols:

$\int$: integral, ${\mathrm{\Gamma }}_q\left(z\right)$: $q$-gamma function, ${(a;q)}_n$: $q$-Pochhammer symbol (or $q$-shifted factorial), $d_{q}x$: $q$-differential, $q$: complex base and $x$: real variable

Permalink:

http://dlmf.nist.gov/17.13.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §17.13 and Ch.17

… ►

17.13.3 $${\int }_0^{\mathrm{\infty }}{t}^{\alpha -1}\frac{{(-t{q}^{\alpha +\beta };q)}_{\mathrm{\infty }}}{{(-t;q)}_{\mathrm{\infty }}}dt=\frac{\mathrm{\Gamma }\left(\alpha \right)\mathrm{\Gamma }\left(1-\alpha \right){\mathrm{\Gamma }}_q\left(\beta \right)}{{\mathrm{\Gamma }}_q\left(1-\alpha \right){\mathrm{\Gamma }}_q\left(\alpha +\beta \right)},$$

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $dx$: differential of $x$ , $\int$: integral, ${\mathrm{\Gamma }}_q\left(z\right)$: $q$-gamma function, ${(a;q)}_n$: $q$-Pochhammer symbol (or $q$-shifted factorial) and $q$: complex base

Referenced by:

Erratum (V1.0.1) for Equation (17.13.3)

Permalink:

http://dlmf.nist.gov/17.13.E3

Encodings:

pMML, png, TeX

Errata (effective with 1.0.1):

Originally the differential was identified incorrectly as a $q$-differential; the correct differential is $dt$.

See also:

Annotations for §17.13, §17.13 and Ch.17

►

17.13.4 $${\int }_0^{\mathrm{\infty }}{t}^{\alpha -1}\frac{{(-ct{q}^{\alpha +\beta };q)}_{\mathrm{\infty }}}{{(-ct;q)}_{\mathrm{\infty }}}{d}_{q}t=\frac{{\mathrm{\Gamma }}_q\left(\alpha \right){\mathrm{\Gamma }}_q\left(\beta \right){(-c{q}^{\alpha };q)}_{\mathrm{\infty }}{(-q^{1-\alpha }/c;q)}_{\mathrm{\infty }}}{{\mathrm{\Gamma }}_q\left(\alpha +\beta \right){(-c;q)}_{\mathrm{\infty }}{(-q/c;q)}_{\mathrm{\infty }}}.$$

ⓘ

Symbols:

$\int$: integral, ${\mathrm{\Gamma }}_q\left(z\right)$: $q$-gamma function, ${(a;q)}_n$: $q$-Pochhammer symbol (or $q$-shifted factorial), $d_{q}x$: $q$-differential and $q$: complex base

Permalink:

http://dlmf.nist.gov/17.13.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §17.13, §17.13 and Ch.17

…

3: 5.12 Beta Function

… ►

Pochhammer’s Integral

►When $a,b\in ℂ$ … ►

►►

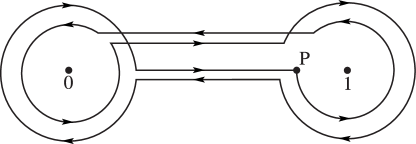
Figure 5.12.3: $t$-plane. Contour for Pochhammer’s integral. Magnify

4: 31.9 Orthogonality

… ►

31.9.2 $${\int }_{\zeta }^{(1+,0+,1-,0-)}{t}^{\gamma -1}{(1-t)}^{\delta -1}{(t-a)}^{ϵ-1}{w}_m(t)w_k(t)dt={\delta }_{m,k}{\theta }_m.$$

ⓘ

Symbols:

${\delta }_{j,k}$: Kronecker delta, $dx$: differential of $x$ , $\int$: integral, $\gamma$: real or complex parameter, $\delta$: real or complex parameter, $ϵ$: real or complex parameter, $m$: nonnegative integer, $a$: complex parameter, $\zeta$: point and ${\theta }_m$: normalization constant

Permalink:

http://dlmf.nist.gov/31.9.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §31.9(i), §31.9 and Ch.31

…

5: 18.28 Askey–Wilson Class

… ►

18.28.8 $$\frac{1}{2\pi }{\int }_0^{\pi }{Q}_n(\cos \theta ;a,b|q)Q_m(\cos \theta ;a,b|q){\left|\frac{{({\mathrm{e}}^{2i\theta };q)}_{\mathrm{\infty }}}{{(a{\mathrm{e}}^{\mathrm{i}\theta },b{\mathrm{e}}^{\mathrm{i}\theta };q)}_{\mathrm{\infty }}}\right|}^{2}d\theta =\frac{{\delta }_{n,m}}{{(q^{n+1},ab{q}^n;q)}_{\mathrm{\infty }}},$$ $a,b\in ℝ$ or $a=\overline{b}$; $ab\ne 1$; $|a|,|b|\le 1$.

ⓘ

Symbols:

$Q_n(x;a,b|q)$: Al-Salam–Chihara polynomial, ${\delta }_{j,k}$: Kronecker delta, $\pi$: the ratio of the circumference of a circle to its diameter, $\overline{z}$: complex conjugate, $\cos z$: cosine function, $dx$: differential of $x$ , $\in$: element of, $\mathrm{e}$: base of natural logarithm, $\mathrm{i}$: imaginary unit, $\int$: integral, ${(a;q)}_n$: $q$-Pochhammer symbol (or $q$-shifted factorial), ${(a_1,a_2,\mathrm{\dots },a_r;q)}_n$: multiple $q$-Pochhammer symbol, $ℝ$: real line, $q$: real variable, $m$: nonnegative integer and $n$: nonnegative integer

Referenced by:

§18.28(iii), Erratum (V1.2.0) for Equation (18.28.8)

Permalink:

http://dlmf.nist.gov/18.28.E8

Encodings:

pMML, png, TeX

Modification (effective with 1.2.0):

The constraint which originally stated that “” has been updated to be “$ab\ne 1$”.

See also:

Annotations for §18.28(iii), §18.28 and Ch.18

… ►

18.28.15 $$\frac{1}{2\pi }{\int }_0^{\pi }{C}_n(\cos \theta ;\beta |q)C_m(\cos \theta ;\beta |q){\left|\frac{{({\mathrm{e}}^{2\mathrm{i}\theta };q)}_{\mathrm{\infty }}}{{(\beta {\mathrm{e}}^{2\mathrm{i}\theta };q)}_{\mathrm{\infty }}}\right|}^{2}d\theta =\frac{{(\beta ,\beta q;q)}_{\mathrm{\infty }}}{{({\beta }^2,q;q)}_{\mathrm{\infty }}}\frac{(1-\beta ){({\beta }^2;q)}_n}{(1-\beta q^n){(q;q)}_n}{\delta }_{n,m},$$ .

ⓘ

Symbols:

${\delta }_{j,k}$: Kronecker delta, $\pi$: the ratio of the circumference of a circle to its diameter, $\cos z$: cosine function, $dx$: differential of $x$ , $\mathrm{e}$: base of natural logarithm, $\mathrm{i}$: imaginary unit, $\int$: integral, ${(a;q)}_n$: $q$-Pochhammer symbol (or $q$-shifted factorial), ${(a_1,a_2,\mathrm{\dots },a_r;q)}_n$: multiple $q$-Pochhammer symbol, $C_n(x;\beta |q)$: continuous $q$-ultraspherical polynomial, $q$: real variable, $m$: nonnegative integer and $n$: nonnegative integer

Permalink:

http://dlmf.nist.gov/18.28.E15

Encodings:

pMML, png, TeX

See also:

Annotations for §18.28(v), §18.28 and Ch.18

… ►

18.28.17 $$\frac{1}{2\pi }{\int }_0^{\pi }{H}_n\left(\cos \theta |q\right)H_m\left(\cos \theta |q\right){\left|{({\mathrm{e}}^{2\mathrm{i}\theta };q)}_{\mathrm{\infty }}\right|}^{2}d\theta =\frac{{\delta }_{n,m}}{{(q^{n+1};q)}_{\mathrm{\infty }}}.$$

ⓘ

Symbols:

${\delta }_{j,k}$: Kronecker delta, $\pi$: the ratio of the circumference of a circle to its diameter, $H_n\left(x|q\right)$: continuous $q$-Hermite polynomial, $\cos z$: cosine function, $dx$: differential of $x$ , $\mathrm{e}$: base of natural logarithm, $\mathrm{i}$: imaginary unit, $\int$: integral, ${(a;q)}_n$: $q$-Pochhammer symbol (or $q$-shifted factorial), $q$: real variable, $m$: nonnegative integer and $n$: nonnegative integer

Permalink:

http://dlmf.nist.gov/18.28.E17

Encodings:

pMML, png, TeX

See also:

Annotations for §18.28(vi), §18.28 and Ch.18

…

6: 19.5 Maclaurin and Related Expansions

… ►

19.5.1 $$K\left(k\right)=\frac{\pi }{2}\sum _{m=0}^{\mathrm{\infty }}\frac{{\left(\frac{1}{2}\right)}_m{\left(\frac{1}{2}\right)}_m}{m!m!}{k}^{2m}=\frac{\pi }{2}{}_2{}^{}F_1^{}(\genfrac{}{}{0pt}{}{\frac{1}{2},\frac{1}{2}}{1};k^2),$$

ⓘ

Symbols:

${}_2{}^{}F_1^{}(a,b;c;z)$: $=F(a,b;c;z)$ notation for Gauss’ hypergeometric function, ${\left(a\right)}_n$: Pochhammer’s symbol (or shifted factorial), $\pi$: the ratio of the circumference of a circle to its diameter, $K\left(k\right)$: Legendre’s complete elliptic integral of the first kind, $!$: factorial (as in $n!$), $m$: nonnegative integer and $k$: real or complex modulus

Source:

Carlson (1961b, (2.4))

Referenced by:

§19.36(iv), §19.5

Permalink:

http://dlmf.nist.gov/19.5.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §19.5 and Ch.19

… ►

19.5.3 $$D\left(k\right)=\frac{\pi }{4}\sum _{m=0}^{\mathrm{\infty }}\frac{{\left(\frac{3}{2}\right)}_m{\left(\frac{1}{2}\right)}_m}{(m+1)!m!}{k}^{2m}=\frac{\pi }{4}{}_2{}^{}F_1^{}(\genfrac{}{}{0pt}{}{\frac{3}{2},\frac{1}{2}}{2};k^2),$$

ⓘ

Symbols:

${}_2{}^{}F_1^{}(a,b;c;z)$: $=F(a,b;c;z)$ notation for Gauss’ hypergeometric function, ${\left(a\right)}_n$: Pochhammer’s symbol (or shifted factorial), $\pi$: the ratio of the circumference of a circle to its diameter, $D\left(k\right)$: complete elliptic integral of Legendre’s type, $!$: factorial (as in $n!$), $m$: nonnegative integer and $k$: real or complex modulus

Permalink:

http://dlmf.nist.gov/19.5.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §19.5 and Ch.19

… ►

19.5.4_1 $$F(\varphi ,k)=\sum _{m=0}^{\mathrm{\infty }}\frac{{\left(\frac{1}{2}\right)}_m{\sin }^{2m+1}\varphi }{(2m+1)m!}{}_2{}^{}F_1^{}(\genfrac{}{}{0pt}{}{m+\frac{1}{2},\frac{1}{2}}{m+\frac{3}{2}};{\sin }^2\varphi )k^{2m}=\sin \varphi F_1(\frac{1}{2};\frac{1}{2},\frac{1}{2};\frac{3}{2};{\sin }^2\varphi ,k^2{\sin }^2\varphi ),$$

ⓘ

Symbols:

$F_1(\alpha ;\beta ,{\beta }^{\prime };\gamma ;x,y)$: first Appell function, ${}_2{}^{}F_1^{}(a,b;c;z)$: $=F(a,b;c;z)$ notation for Gauss’ hypergeometric function, ${\left(a\right)}_n$: Pochhammer’s symbol (or shifted factorial), $F(\varphi ,k)$: Legendre’s incomplete elliptic integral of the first kind, $!$: factorial (as in $n!$), $\sin z$: sine function, $m$: nonnegative integer, $\varphi$: real or complex argument and $k$: real or complex modulus

Source:

Carlson (1961b, (2.8))

Referenced by:

§19.5, Erratum (V1.1.2) for Additions

Permalink:

http://dlmf.nist.gov/19.5.E4_1

Encodings:

pMML, png, TeX

Addition (effective with 1.1.2):

This equation was added.

See also:

Annotations for §19.5 and Ch.19

►

19.5.4_2 $$E(\varphi ,k)=\sum _{m=0}^{\mathrm{\infty }}\frac{{\left(-\frac{1}{2}\right)}_m{\sin }^{2m+1}\varphi }{(2m+1)m!}{}_2{}^{}F_1^{}(\genfrac{}{}{0pt}{}{m+\frac{1}{2},\frac{1}{2}}{m+\frac{3}{2}};{\sin }^2\varphi )k^{2m}=\sin \varphi F_1(\frac{1}{2};\frac{1}{2},-\frac{1}{2};\frac{3}{2};{\sin }^2\varphi ,k^2{\sin }^2\varphi ),$$

ⓘ

Symbols:

$F_1(\alpha ;\beta ,{\beta }^{\prime };\gamma ;x,y)$: first Appell function, ${}_2{}^{}F_1^{}(a,b;c;z)$: $=F(a,b;c;z)$ notation for Gauss’ hypergeometric function, ${\left(a\right)}_n$: Pochhammer’s symbol (or shifted factorial), $E(\varphi ,k)$: Legendre’s incomplete elliptic integral of the second kind, $!$: factorial (as in $n!$), $\sin z$: sine function, $m$: nonnegative integer, $\varphi$: real or complex argument and $k$: real or complex modulus

Source:

Carlson (1961b, (2.9))

Referenced by:

§19.5, Erratum (V1.1.2) for Additions

Permalink:

http://dlmf.nist.gov/19.5.E4_2

Encodings:

pMML, png, TeX

Addition (effective with 1.1.2):

This equation was added.

See also:

Annotations for §19.5 and Ch.19

►

19.5.4_3 $$\mathrm{\Pi }(\varphi ,{\alpha }^2,k)=\sum _{m=0}^{\mathrm{\infty }}\frac{{\left(\frac{1}{2}\right)}_m{\sin }^{2m+1}\varphi }{(2m+1)m!}{F}_1(m+\frac{1}{2};\frac{1}{2},1;m+\frac{3}{2};{\sin }^2\varphi ,{\alpha }^2{\sin }^2\varphi )k^{2m},$$

ⓘ

Symbols:

$F_1(\alpha ;\beta ,{\beta }^{\prime };\gamma ;x,y)$: first Appell function, ${\left(a\right)}_n$: Pochhammer’s symbol (or shifted factorial), $\mathrm{\Pi }(\varphi ,{\alpha }^2,k)$: Legendre’s incomplete elliptic integral of the third kind, $!$: factorial (as in $n!$), $\sin z$: sine function, $m$: nonnegative integer, $\varphi$: real or complex argument, $k$: real or complex modulus and ${\alpha }^2$: real or complex parameter

Source:

Carlson (1961b, (2.11))

Referenced by:

§19.5, Erratum (V1.1.2) for Additions

Permalink:

http://dlmf.nist.gov/19.5.E4_3

Encodings:

pMML, png, TeX

Addition (effective with 1.1.2):

This equation was added.

See also:

Annotations for §19.5 and Ch.19

…

7: 19.12 Asymptotic Approximations

… ►

19.12.1 $$K\left(k\right)=\sum _{m=0}^{\mathrm{\infty }}\frac{{\left(\frac{1}{2}\right)}_m{\left(\frac{1}{2}\right)}_m}{m!m!}k_{}^{\prime }{}_{}{}^{2m}\left(\ln \left(\frac{1}{k^{\prime }}\right)+d(m)\right),$$ ,

ⓘ

Symbols:

${\left(a\right)}_n$: Pochhammer’s symbol (or shifted factorial), $K\left(k\right)$: Legendre’s complete elliptic integral of the first kind, $!$: factorial (as in $n!$), $\ln z$: principal branch of logarithm function, $m$: nonnegative integer, $k$: real or complex modulus, $k^{\prime }$: complementary modulus and $d(m)$: function

Referenced by:

§19.12

Permalink:

http://dlmf.nist.gov/19.12.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §19.12 and Ch.19

►

19.12.2 $$E\left(k\right)=1+\frac{1}{2}\sum _{m=0}^{\mathrm{\infty }}\frac{{\left(\frac{1}{2}\right)}_m{\left(\frac{3}{2}\right)}_m}{{\left(2\right)}_{m}m!}k_{}^{\prime }{}_{}{}^{2m+2}\left(\ln \left(\frac{1}{k^{\prime }}\right)+d(m)-\frac{1}{(2m+1)(2m+2)}\right),$$ ,

ⓘ

Symbols:

${\left(a\right)}_n$: Pochhammer’s symbol (or shifted factorial), $E\left(k\right)$: Legendre’s complete elliptic integral of the second kind, $!$: factorial (as in $n!$), $\ln z$: principal branch of logarithm function, $m$: nonnegative integer, $k$: real or complex modulus, $k^{\prime }$: complementary modulus and $d(m)$: function

Referenced by:

§19.12

Permalink:

http://dlmf.nist.gov/19.12.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §19.12 and Ch.19

…

8: 25.5 Integral Representations

… ►

25.5.7 $$\zeta \left(s\right)=\frac{1}{2}+\frac{1}{s-1}+\sum _{m=1}^n\frac{B_{2m}}{(2m)!}{\left(s\right)}_{2m-1}+\frac{1}{\mathrm{\Gamma }\left(s\right)}{\int }_0^{\mathrm{\infty }}\left(\frac{1}{{\mathrm{e}}^x-1}-\frac{1}{x}+\frac{1}{2}-\sum _{m=1}^n\frac{B_{2m}}{(2m)!}{x}^{2m-1}\right)\frac{x^{s-1}}{{\mathrm{e}}^x}dx,$$ $\mathrm{\Re }s>-(2n+1)$, $n=1,2,3,\mathrm{\dots }$.

ⓘ

Symbols:

$B_n$: Bernoulli numbers, $O\left(x\right)$: order not exceeding, $\mathrm{\Gamma }\left(z\right)$: gamma function, ${\left(a\right)}_n$: Pochhammer’s symbol (or shifted factorial), $\zeta \left(s\right)$: Riemann zeta function, $dx$: differential of $x$ , $\mathrm{e}$: base of natural logarithm, $!$: factorial (as in $n!$), $\int$: integral, $\mathrm{\Re }$: real part, $m$: nonnegative integer, $n$: nonnegative integer, $x$: real variable and $s$: complex variable

Keywords:

improper integral, integral representation

Proof sketch:

Derivable from (25.5.6) by adding and subtracting ${\sum }_{m=1}^n{B}_{2m}{x}^{2m-1}/(2m)!$ in the integrand, using (5.2.1), (5.2.5), and recognizing that ${({\mathrm{e}}^x-1)}^{-1}-x^{-1}+1/2-{\sum }_{m=1}^n{B}_{2m}{x}^{2m-1}/(2m)!=O\left(x^{2n+1}\right)$ as $x\to 0$, demonstrating the region of convergence.

Referenced by:

Erratum (V1.0.9) for Chapters 7, 25

Permalink:

http://dlmf.nist.gov/25.5.E7

Encodings:

pMML, png, TeX

Notational Change (effective with 1.0.9):

We have rewritten the original summation ${\sum }_{m=1}^n\frac{B_{2m}}{(2m)!}\frac{\mathrm{\Gamma }\left(s+2m-1\right)}{\mathrm{\Gamma }\left(s\right)}$ more concisely as ${\sum }_{m=1}^n\frac{B_{2m}}{(2m)!}{\left(s\right)}_{2m-1}$ using the Pochhammer symbol.

See also:

Annotations for §25.5(i), §25.5 and Ch.25

…

9: 8.20 Asymptotic Expansions of $E_p\left(z\right)$

… ►

8.20.1 $$E_p\left(z\right)=\frac{{\mathrm{e}}^{-z}}{z}\left(\sum _{k=0}^{n-1}{(-1)}^k\frac{{\left(p\right)}_k}{z^k}+{(-1)}^n\frac{{\left(p\right)}_n{\mathrm{e}}^z}{z^{n-1}}{E}_{n+p}\left(z\right)\right),$$ $n=1,2,3,\mathrm{\dots }$.

ⓘ

Symbols:

${\left(a\right)}_n$: Pochhammer’s symbol (or shifted factorial), $\mathrm{e}$: base of natural logarithm, $E_p\left(z\right)$: generalized exponential integral, $z$: complex variable, $p$: parameter, $k$: nonnegative integer and $n$: nonnegative integer

A&S Ref:

5.1.51

Permalink:

http://dlmf.nist.gov/8.20.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §8.20(i), §8.20 and Ch.8

… ►

8.20.2 $$E_p\left(z\right)\sim \frac{{\mathrm{e}}^{-z}}{z}\sum _{k=0}^{\mathrm{\infty }}{(-1)}^k\frac{{\left(p\right)}_k}{z^k},$$ $|\mathrm{ph}z|\le \frac{3}{2}\pi -\delta$,

ⓘ

Symbols:

${\left(a\right)}_n$: Pochhammer’s symbol (or shifted factorial), $\sim$: Poincaré asymptotic expansion, $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{e}$: base of natural logarithm, $E_p\left(z\right)$: generalized exponential integral, $\mathrm{ph}$: phase, $z$: complex variable, $p$: parameter, $k$: nonnegative integer and $\delta$: small positive constant

Referenced by:

§8.20(i)

Permalink:

http://dlmf.nist.gov/8.20.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §8.20(i), §8.20 and Ch.8

… ►

8.20.3 $$E_p\left(z\right)\sim \pm \frac{2\pi \mathrm{i}}{\mathrm{\Gamma }\left(p\right)}{\mathrm{e}}^{\mp p\pi \mathrm{i}}{z}^{p-1}+\frac{{\mathrm{e}}^{-z}}{z}\sum _{k=0}^{\mathrm{\infty }}\frac{{(-1)}^k{\left(p\right)}_k}{z^k},$$ $\frac{1}{2}\pi +\delta \le \pm \mathrm{ph}z\le \frac{7}{2}\pi -\delta$,

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, ${\left(a\right)}_n$: Pochhammer’s symbol (or shifted factorial), $\sim$: Poincaré asymptotic expansion, $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{e}$: base of natural logarithm, $E_p\left(z\right)$: generalized exponential integral, $\mathrm{i}$: imaginary unit, $\mathrm{ph}$: phase, $z$: complex variable, $p$: parameter, $k$: nonnegative integer and $\delta$: small positive constant

Referenced by:

§2.11(ii), §8.20(i)

Permalink:

http://dlmf.nist.gov/8.20.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §8.20(i), §8.20 and Ch.8

…

10: 8.21 Generalized Sine and Cosine Integrals

… ►

8.21.16 $$\mathrm{Si}(a,z)=z^a\sum _{k=0}^{\mathrm{\infty }}\frac{\left(2k+\frac{3}{2}\right){\left(1-\frac{1}{2}a\right)}_k}{{\left(\frac{1}{2}+\frac{1}{2}a\right)}_{k+1}}{𝗃}_{2k+1}\left(z\right),$$ $a\ne -1,-3,-5,\mathrm{\dots }$,

ⓘ

Symbols:

${\left(a\right)}_n$: Pochhammer’s symbol (or shifted factorial), $\mathrm{Si}(a,z)$: generalized sine integral, ${𝗃}_n\left(z\right)$: spherical Bessel function of the first kind, $z$: complex variable, $a$: parameter and $k$: nonnegative integer

Referenced by:

§8.21(vi)

Permalink:

http://dlmf.nist.gov/8.21.E16

Encodings:

pMML, png, TeX

See also:

Annotations for §8.21(vi), §8.21(vi), §8.21 and Ch.8

►

8.21.17 $$\mathrm{Ci}(a,z)=z^a\sum _{k=0}^{\mathrm{\infty }}\frac{\left(2k+\frac{1}{2}\right){\left(\frac{1}{2}-\frac{1}{2}a\right)}_k}{{\left(\frac{1}{2}a\right)}_{k+1}}{𝗃}_{2k}\left(z\right),$$ $a\ne 0,-2,-4,\mathrm{\dots }$.

ⓘ

Symbols:

${\left(a\right)}_n$: Pochhammer’s symbol (or shifted factorial), $\mathrm{Ci}(a,z)$: generalized cosine integral, ${𝗃}_n\left(z\right)$: spherical Bessel function of the first kind, $z$: complex variable, $a$: parameter and $k$: nonnegative integer

Referenced by:

§8.21(vi)

Permalink:

http://dlmf.nist.gov/8.21.E17

Encodings:

pMML, png, TeX

See also:

Annotations for §8.21(vi), §8.21(vi), §8.21 and Ch.8

…