beta function

SearchAdvancedHelp

(0.008 seconds)

1—10 of 179 matching pages

1: 5.12 Beta Function

§5.12 Beta Function

… ►

Euler’s Beta Integral

… ►

►►

Figure 5.12.1: $t$-plane. Contour for first loop integral for the beta function. Magnify

… ►

►►

Figure 5.12.2: $t$-plane. Contour for second loop integral for the beta function. Magnify

►

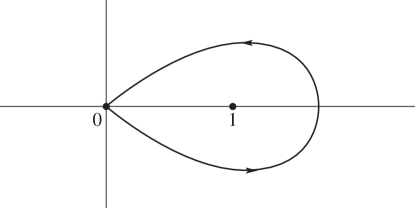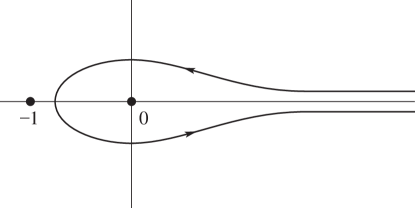Pochhammer’s Integral

…

2: 8.17 Incomplete Beta Functions

§8.17 Incomplete Beta Functions

… ►

§8.17(ii) Hypergeometric Representations

… ►

§8.17(iii) Integral Representation

… ►

§8.17(iv) Recurrence Relations

… ►

§8.17(vi) Sums

…

3: 8.23 Statistical Applications

§8.23 Statistical Applications

… ►The function ${\mathrm{B}}_x(a,b)$ and its normalization $I_x(a,b)$ play a similar role in statistics in connection with the beta distribution; see Johnson et al. (1995, pp. 210–275). …

4: 8.24 Physical Applications

§8.24 Physical Applications

… ►

§8.24(ii) Incomplete Beta Functions

…

5: 5.20 Physical Applications

§5.20 Physical Applications

… ►Then the partition function (with $\beta =1/(kT)$) is given by … ►

Elementary Particles

►Veneziano (1968) identifies relationships between particle scattering amplitudes described by the beta function, an important early development in string theory. …

6: 8.26 Tables

… ►

§8.26(iii) Incomplete Beta Functions

…

7: 5.18 $q$-Gamma and $q$-Beta Functions

§5.18 $q$-Gamma and $q$-Beta Functions

… ►

§5.18(iii) $q$-Beta Function

►

5.18.11 $${\mathrm{B}}_q(a,b)=\frac{{\mathrm{\Gamma }}_q\left(a\right){\mathrm{\Gamma }}_q\left(b\right)}{{\mathrm{\Gamma }}_q\left(a+b\right)}.$$

ⓘ

Defines:

${\mathrm{B}}_q(a,b)$: $q$-beta function

Symbols:

${\mathrm{\Gamma }}_q\left(z\right)$: $q$-gamma function, $q$: real or complex variable, $a$: real or complex variable and $b$: real or complex variable

Permalink:

http://dlmf.nist.gov/5.18.E11

Encodings:

pMML, png, TeX

See also:

Annotations for §5.18(iii), §5.18 and Ch.5

►

5.18.12 $${\mathrm{B}}_q(a,b)={\int }_0^1\frac{t^{a-1}{(tq;q)}_{\mathrm{\infty }}}{{(t{q}^b;q)}_{\mathrm{\infty }}}{d}_{q}t,$$ , $\mathrm{\Re }a>0$, $\mathrm{\Re }b>0$.

ⓘ

Symbols:

$\int$: integral, ${\mathrm{B}}_q(a,b)$: $q$-beta function, ${(a;q)}_n$: $q$-Pochhammer symbol (or $q$-shifted factorial), $d_{q}x$: $q$-differential, $\mathrm{\Re }$: real part, $q$: real or complex variable, $a$: real or complex variable and $b$: real or complex variable

Permalink:

http://dlmf.nist.gov/5.18.E12

Encodings:

pMML, png, TeX

See also:

Annotations for §5.18(iii), §5.18 and Ch.5

…

8: 35.3 Multivariate Gamma and Beta Functions

§35.3 Multivariate Gamma and Beta Functions

… ►

35.3.3 $\mathrm{\Re }\left(a\right),\mathrm{\Re }\left(b\right)>\frac{1}{2}(m-1)$.

ⓘ

Defines:

${\mathrm{B}}_m(a,b)$: multivariate beta function

Symbols:

$\int$: integral, $\mathrm{\Re }$: real part, $a$: complex variable, $𝐈$: $m\times m$ identity matrix, $𝐗$: real symmetric $m\times m$ matrix, $\left|𝐗\right|$: determinant of $𝐗$ , $d$: differential of matrix, $b$: complex variable, : less-than for matrices, $m$: positive integer and $𝟎$: $m\times m$ matrix of zeros

Keywords:

definition, multivariate betafunction

Permalink:

http://dlmf.nist.gov/35.3.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §35.3(i), §35.3 and Ch.35

… ►

35.3.6 $${\mathrm{\Gamma }}_m\left(a,\mathrm{\dots },a\right)={\mathrm{\Gamma }}_m\left(a\right).$$

ⓘ

Symbols:

${\mathrm{\Gamma }}_m\left(a\right)$: multivariate gamma function, $a$: complex variable and $m$: positive integer

Permalink:

http://dlmf.nist.gov/35.3.E6

Encodings:

pMML, png, TeX

See also:

Annotations for §35.3(ii), §35.3 and Ch.35

►

35.3.7 $${\mathrm{B}}_m(a,b)=\frac{{\mathrm{\Gamma }}_m\left(a\right){\mathrm{\Gamma }}_m\left(b\right)}{{\mathrm{\Gamma }}_m\left(a+b\right)}.$$

ⓘ

Symbols:

${\mathrm{B}}_m(a,b)$: multivariate beta function, ${\mathrm{\Gamma }}_m\left(a\right)$: multivariate gamma function, $a$: complex variable, $b$: complex variable and $m$: positive integer

Permalink:

http://dlmf.nist.gov/35.3.E7

Encodings:

pMML, png, TeX

See also:

Annotations for §35.3(ii), §35.3 and Ch.35

►

35.3.8 $${\mathrm{B}}_m(a,b)={\int }_{𝛀}{\left|𝐗\right|}^{a-\frac{1}{2}(m+1)}{\left|𝐈+𝐗\right|}^{-(a+b)}d𝐗,$$ $\mathrm{\Re }\left(a\right),\mathrm{\Re }\left(b\right)>\frac{1}{2}(m-1)$.

ⓘ

Symbols:

$\int$: integral, ${\mathrm{B}}_m(a,b)$: multivariate beta function, $\mathrm{\Re }$: real part, $a$: complex variable, $𝐈$: $m\times m$ identity matrix, $𝐗$: real symmetric $m\times m$ matrix, $\left|𝐗\right|$: determinant of $𝐗$ , $d$: differential of matrix, $𝛀$: space of positive-definite real symmetric $m\times m$ matrices, $b$: complex variable and $m$: positive integer

Permalink:

http://dlmf.nist.gov/35.3.E8

Encodings:

pMML, png, TeX

See also:

Annotations for §35.3(ii), §35.3 and Ch.35

9: 8.18 Asymptotic Expansions of $I_x(a,b)$

… ►

8.18.1 $$I_x(a,b)=\mathrm{\Gamma }\left(a+b\right)x^a{(1-x)}^{b-1}\left(\sum _{k=0}^{n-1}\frac{1}{\mathrm{\Gamma }\left(a+k+1\right)\mathrm{\Gamma }\left(b-k\right)}{\left(\frac{x}{1-x}\right)}^k+O\left(\frac{1}{\mathrm{\Gamma }\left(a+n+1\right)}\right)\right),$$

ⓘ

Symbols:

$O\left(x\right)$: order not exceeding, $\mathrm{\Gamma }\left(z\right)$: gamma function, $I_x(a,b)$: incomplete beta function, $k$: nonnegative integer, $n$: nonnegative integer, $a$: parameter, $b$: parameter and $x$: variable

Referenced by:

§8.18(i)

Permalink:

http://dlmf.nist.gov/8.18.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §8.18(i), §8.18 and Ch.8

… ►

Symmetric Case

… ►

General Case

… ►

Inverse Function

… ►

8.18.18 $$I_x(a,b)=p,$$ $0\le p\le 1$,

ⓘ

Symbols:

$I_x(a,b)$: incomplete beta function, $p$: parameter, $a$: parameter, $b$: parameter and $x$: variable

Permalink:

http://dlmf.nist.gov/8.18.E18

Encodings:

pMML, png, TeX

See also:

Annotations for §8.18(ii), §8.18(ii), §8.18 and Ch.8

…

10: 8.1 Special Notation

… ►Unless otherwise indicated, primes denote derivatives with respect to the argument. ►The functions treated in this chapter are the incomplete gamma functions $\gamma (a,z)$, $\mathrm{\Gamma }(a,z)$, ${\gamma }^{\ast }(a,z)$, $P(a,z)$, and $Q(a,z)$; the incomplete beta functions ${\mathrm{B}}_x(a,b)$ and $I_x(a,b)$; the generalized exponential integral $E_p\left(z\right)$; the generalized sine and cosine integrals $\mathrm{si}(a,z)$, $\mathrm{ci}(a,z)$, $\mathrm{Si}(a,z)$, and $\mathrm{Ci}(a,z)$. ►Alternative notations include: Prym’s functions $P_z(a)=\gamma (a,z)$, $Q_z(a)=\mathrm{\Gamma }(a,z)$, Nielsen (1906a, pp. 25–26), Batchelder (1967, p. 63); $(a,z)!=\gamma (a+1,z)$, $[a,z]!=\mathrm{\Gamma }(a+1,z)$, Dingle (1973); $B(a,b,x)={\mathrm{B}}_x(a,b)$, $I(a,b,x)=I_x(a,b)$, Magnus et al. (1966); $\mathrm{Si}(a,x)\to \mathrm{Si}(1-a,x)$, $\mathrm{Ci}(a,x)\to \mathrm{Ci}(1-a,x)$, Luke (1975).