§18.21 Hahn Class: Interrelations

Keywords:: Hahn class orthogonal polynomials
Permalink:: http://dlmf.nist.gov/18.21

§18.21(i) Dualities
§18.21(ii) Limit Relations and Special Cases

§18.21(i) Dualities

Keywords:: Hahn class orthogonal polynomials, Wilson class orthogonal polynomials
Permalink:: http://dlmf.nist.gov/18.21.i

¶ Duality of Hahn and Dual Hahn

18.21.1 $\mathop{Q_{{n}}\/}\nolimits\!\left(x;\alpha,\beta,N\right)=\mathop{R_{{x}}\/}\nolimits\!\left(n(n+\alpha+\beta+1);\alpha,\beta,N\right),$ $n,x=0,1,\dots,N$ .

Symbols:: $\mathop{Q_{{n}}\/}\nolimits\!\left(x;\alpha,\beta,N\right)$ : Hahn polynomial, $\mathop{R_{{n}}\/}\nolimits\!\left(x;\gamma,\delta,N\right)$ : dual Hahn polynomial, $n$ : nonnegative integer, $N$ : positive integer and $x$ : real variable
Referenced by:: §18.21(ii)
Permalink:: http://dlmf.nist.gov/18.21.E1
Encodings:: TeX, pMML, png

For the dual Hahn polynomial $\mathop{R_{{n}}\/}\nolimits\!\left(x;\gamma,\delta,N\right)$ see §18.25.

¶ Self-Dualities

18.21.2

$\mathop{K_{{n}}\/}\nolimits\!\left(x;p,N\right)=\mathop{K_{{x}}\/}\nolimits\!\left(n;p,N\right),$ $n,x=0,1,\dots,N$ .

$\mathop{M_{{n}}\/}\nolimits\!\left(x;\beta,c\right)=\mathop{M_{{x}}\/}\nolimits\!\left(n;\beta,c\right),$ $n,x=0,1,2,\dots$ .

$\mathop{C_{{n}}\/}\nolimits\!\left(x,a\right)=\mathop{C_{{x}}\/}\nolimits\!\left(n,a\right),$ $n,x=0,1,2,\dots$ .

Symbols:: $\mathop{C_{{n}}\/}\nolimits\!\left(x,a\right)$ : Charlier polynomial, $\mathop{K_{{n}}\/}\nolimits\!\left(x;p,N\right)$ : Krawtchouk polynomial, $\mathop{M_{{n}}\/}\nolimits\!\left(x;\beta,c\right)$ : Meixner polynomial, $n$ : nonnegative integer, $N$ : positive integer and $x$ : real variable
Referenced by:: §18.21(ii), §18.22(ii)
Permalink:: http://dlmf.nist.gov/18.21.E2
Encodings:: TeX, TeX, TeX, pMML, pMML, pMML, png, png, png

§18.21(ii) Limit Relations and Special Cases

Notes:: For (18.21.3), (18.21.5), (18.21.7), (18.21.8) see Ismail (2005, §6.2, unnumbered formula after (6.2.34), also (6.2.17), (6.1.19), (6.1.18)). For (18.21.1) see Karlin and McGregor (1961, (1.19)). The three identities in (18.21.2) follow from (18.20.6), (18.20.7), (18.20.8). (18.21.4) follows from (18.20.5) and (18.20.7). (18.21.6) follows from (18.20.6) and (18.20.8). (18.21.9) follows from (18.22.2), Row 4 in Table 18.22.1, (18.9.1), and Row 10 in Table 18.9.1. (18.21.10) follows from (18.20.9) and (18.20.10). For (18.21.11) see Koornwinder (1989, (2.6)). (18.21.12) follows from (18.20.10) and (18.5.12). For Figure 18.21.1 see Askey and Wilson (1985, p. 46), together with correction in Askey (1985).
Keywords:: Hahn class orthogonal polynomials
Referenced by:: ¶ ‣ §18.21(ii)
Permalink:: http://dlmf.nist.gov/18.21.ii

¶ Hahn $\to$ Krawtchouk

18.21.3 $\lim _{{t\to\infty}}\mathop{Q_{{n}}\/}\nolimits\!\left(x;pt,(1-p)t,N\right)=\mathop{K_{{n}}\/}\nolimits\!\left(x;p,N\right).$

Symbols:: $\mathop{Q_{{n}}\/}\nolimits\!\left(x;\alpha,\beta,N\right)$ : Hahn polynomial, $\mathop{K_{{n}}\/}\nolimits\!\left(x;p,N\right)$ : Krawtchouk polynomial, $n$ : nonnegative integer, $N$ : positive integer and $x$ : real variable
Referenced by:: §18.21(ii)
Permalink:: http://dlmf.nist.gov/18.21.E3
Encodings:: TeX, pMML, png

¶ Hahn $\to$ Meixner

18.21.4 $\lim _{{N\to\infty}}\mathop{Q_{{n}}\/}\nolimits\!\left(x;b-1,N(c^{{-1}}-1),N\right)=\mathop{M_{{n}}\/}\nolimits\!\left(x;b,c\right).$

Symbols:: $\mathop{Q_{{n}}\/}\nolimits\!\left(x;\alpha,\beta,N\right)$ : Hahn polynomial, $\mathop{M_{{n}}\/}\nolimits\!\left(x;\beta,c\right)$ : Meixner polynomial, $n$ : nonnegative integer, $N$ : positive integer and $x$ : real variable
Referenced by:: §18.21(ii)
Permalink:: http://dlmf.nist.gov/18.21.E4
Encodings:: TeX, pMML, png

¶ Hahn $\to$ Jacobi

Keywords:: Jacobi polynomials

18.21.5 $\lim _{{N\to\infty}}\mathop{Q_{{n}}\/}\nolimits\!\left(Nx;\alpha,\beta,N\right)=\frac{\mathop{P^{{(\alpha,\beta)}}_{{n}}\/}\nolimits\!\left(1-2x\right)}{\mathop{P^{{(\alpha,\beta)}}_{{n}}\/}\nolimits\!\left(1\right)}.$

Symbols:: $\mathop{Q_{{n}}\/}\nolimits\!\left(x;\alpha,\beta,N\right)$ : Hahn polynomial, $\mathop{P^{{(\alpha,\beta)}}_{{n}}\/}\nolimits\!\left(x\right)$ : Jacobi polynomial, $n$ : nonnegative integer, $N$ : positive integer and $x$ : real variable
Referenced by:: §18.21(ii)
Permalink:: http://dlmf.nist.gov/18.21.E5
Encodings:: TeX, pMML, png

¶ Krawtchouk $\to$ Charlier

18.21.6 $\lim _{{N\to\infty}}\mathop{K_{{n}}\/}\nolimits\!\left(x;N^{{-1}}a,N\right)=\mathop{C_{{n}}\/}\nolimits\!\left(x,a\right).$

Symbols:: $\mathop{C_{{n}}\/}\nolimits\!\left(x,a\right)$ : Charlier polynomial, $\mathop{K_{{n}}\/}\nolimits\!\left(x;p,N\right)$ : Krawtchouk polynomial, $n$ : nonnegative integer, $N$ : positive integer and $x$ : real variable
Referenced by:: §18.21(ii)
Permalink:: http://dlmf.nist.gov/18.21.E6
Encodings:: TeX, pMML, png

¶ Meixner $\to$ Charlier

18.21.7 $\lim _{{\beta\to\infty}}\mathop{M_{{n}}\/}\nolimits\!\left(x;\beta,a(a+\beta)^{{-1}}\right)=\mathop{C_{{n}}\/}\nolimits\!\left(x,a\right).$

Symbols:: $\mathop{C_{{n}}\/}\nolimits\!\left(x,a\right)$ : Charlier polynomial, $\mathop{M_{{n}}\/}\nolimits\!\left(x;\beta,c\right)$ : Meixner polynomial, $n$ : nonnegative integer and $x$ : real variable
Referenced by:: §18.21(ii), §18.22(iii)
Permalink:: http://dlmf.nist.gov/18.21.E7
Encodings:: TeX, pMML, png

¶ Meixner $\to$ Laguerre

Keywords:: Laguerre polynomials

18.21.8 $\lim _{{c\to 1}}\mathop{M_{{n}}\/}\nolimits\!\left((1-c)^{{-1}}x;\alpha+1,c\right)=\frac{\mathop{L^{{(\alpha)}}_{{n}}\/}\nolimits\!\left(x\right)}{\mathop{L^{{(\alpha)}}_{{n}}\/}\nolimits\!\left(0\right)}.$

Symbols:: $\mathop{M_{{n}}\/}\nolimits\!\left(x;\beta,c\right)$ : Meixner polynomial, $\mathop{L^{{(\alpha)}}_{{n}}\/}\nolimits\!\left(x\right)$ : Laguerre (or generalized Laguerre) polynomial, $n$ : nonnegative integer and $x$ : real variable
Referenced by:: §18.21(ii)
Permalink:: http://dlmf.nist.gov/18.21.E8
Encodings:: TeX, pMML, png

¶ Charlier $\to$ Hermite

Keywords:: Hermite polynomials

18.21.9 $\lim _{{a\to\infty}}(2a)^{{\frac{1}{2}n}}\mathop{C_{{n}}\/}\nolimits\!\left((2a)^{{\frac{1}{2}}}x+a,a\right)=(-1)^{n}\mathop{H_{{n}}\/}\nolimits\!\left(x\right).$

Symbols:: $\mathop{C_{{n}}\/}\nolimits\!\left(x,a\right)$ : Charlier polynomial, $\mathop{H_{{n}}\/}\nolimits\!\left(x\right)$ : Hermite polynomial, $n$ : nonnegative integer and $x$ : real variable
Referenced by:: §18.21(ii)
Permalink:: http://dlmf.nist.gov/18.21.E9
Encodings:: TeX, pMML, png

¶ Continuous Hahn $\to$ Meixner–Pollaczek

18.21.10 $\lim _{{t\to\infty}}t^{{-n}}\mathop{p_{{n}}\/}\nolimits\!\left(x-t;\lambda+it,-t\mathop{\tan\/}\nolimits\phi,\lambda-it,-t\mathop{\tan\/}\nolimits\phi\right)=\frac{(-1)^{n}}{(\mathop{\cos\/}\nolimits\phi)^{n}}\mathop{P^{{(\lambda)}}_{{n}}\/}\nolimits\!\left(x;\phi\right).$

Symbols:: $\mathop{P^{{(\lambda)}}_{{n}}\/}\nolimits\!\left(x;\phi\right)$ : Meixner–Pollaczek polynomial, $\mathop{p_{{n}}\/}\nolimits\!\left(x;a,b,\conj{a},\conj{b}\right)$ : continuous Hahn polynomial, $\mathop{\cos\/}\nolimits z$ : cosine function, $\mathop{\tan\/}\nolimits z$ : tangent function, $n$ : nonnegative integer and $x$ : real variable
Referenced by:: §18.21(ii), §18.22(ii), §18.22(iii)
Permalink:: http://dlmf.nist.gov/18.21.E10
Encodings:: TeX, pMML, png

18.21.11 $\mathop{p_{{n}}\/}\nolimits\!\left(x;a,a+\tfrac{1}{2},a,a+\tfrac{1}{2}\right)=2^{{-2n}}\left(4a+n\right)_{{n}}\mathop{P^{{(2a)}}_{{n}}\/}\nolimits\!\left(2x;\tfrac{1}{2}\pi\right).$

Symbols:: $\mathop{P^{{(\lambda)}}_{{n}}\/}\nolimits\!\left(x;\phi\right)$ : Meixner–Pollaczek polynomial, $\left(a\right)_{{n}}$ : Pochhammer’s symbol, $\mathop{p_{{n}}\/}\nolimits\!\left(x;a,b,\conj{a},\conj{b}\right)$ : continuous Hahn polynomial, $n$ : nonnegative integer and $x$ : real variable
Referenced by:: §18.21(ii)
Permalink:: http://dlmf.nist.gov/18.21.E11
Encodings:: TeX, pMML, png

¶ Meixner–Pollaczek $\to$ Laguerre

Keywords:: Laguerre polynomials

18.21.12 $\lim _{{\phi\to 0}}\mathop{P^{{(\frac{1}{2}\alpha+\frac{1}{2})}}_{{n}}\/}\nolimits\!\left(-(2\phi)^{{-1}}x;\phi\right)=\mathop{L^{{(\alpha)}}_{{n}}\/}\nolimits\!\left(x\right).$

Symbols:: $\mathop{P^{{(\lambda)}}_{{n}}\/}\nolimits\!\left(x;\phi\right)$ : Meixner–Pollaczek polynomial, $\mathop{L^{{(\alpha)}}_{{n}}\/}\nolimits\!\left(x\right)$ : Laguerre (or generalized Laguerre) polynomial, $n$ : nonnegative integer and $x$ : real variable
Referenced by:: §18.21(ii), ¶ ‣ §18.24
Permalink:: http://dlmf.nist.gov/18.21.E12
Encodings:: TeX, pMML, png

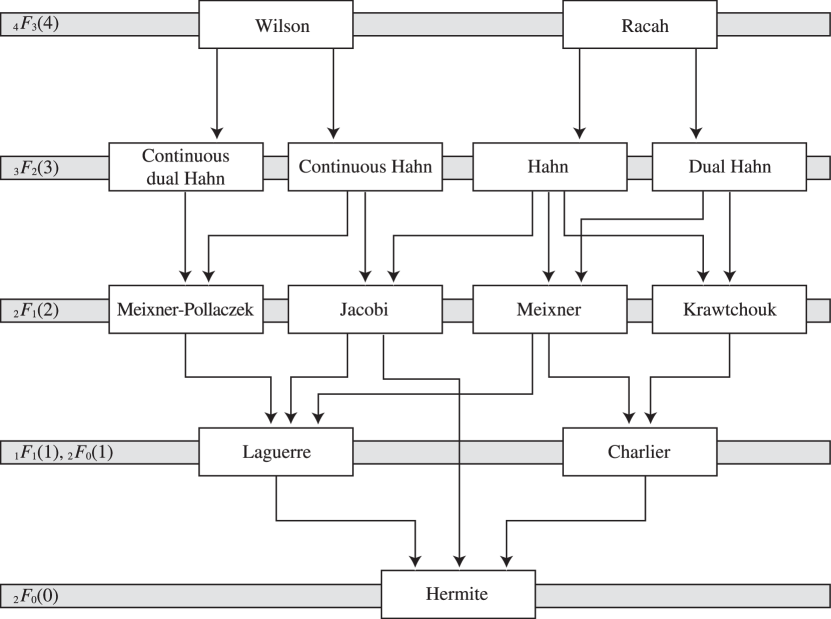
A graphical representation of limits in §§18.7(iii), 18.21(ii), and 18.26(ii) is provided by the Askey scheme depicted in Figure 18.21.1.

Figure 18.21.1: Askey scheme. The number of free real parameters is zero for Hermite polynomials. It increases by one for each row ascended in the scheme, culminating with four free real parameters for the Wilson and Racah polynomials. (This is with the convention that the real and imaginary parts of the parameters are counted separately in the case of the continuous Hahn polynomials.)

Keywords:: Askey–Wilson class orthogonal polynomials, Askey scheme for orthogonal polynomials, Hahn class orthogonal polynomials, Hermite polynomials, Jacobi polynomials, Laguerre polynomials, Wilson class orthogonal polynomials, classical orthogonal polynomials
Referenced by:: ¶ ‣ §18.21(ii), §18.21(ii), ¶ ‣ §18.26(ii), ¶ ‣ §18.7(iii)
Permalink:: http://dlmf.nist.gov/18.21.F1
Encodings:: pdf, png

§18.21 Hahn Class: Interrelations

Contents

§18.21(i) Dualities

¶ Duality of Hahn and Dual Hahn

¶ Self-Dualities

§18.21(ii) Limit Relations and Special Cases

¶ Hahn Krawtchouk

¶ Hahn Meixner

¶ Hahn Jacobi

¶ Krawtchouk Charlier

¶ Meixner Charlier

¶ Meixner Laguerre

¶ Charlier Hermite

¶ Continuous Hahn Meixner–Pollaczek

¶ Meixner–Pollaczek Laguerre