Euler%E2%80%93Maclaurin

SearchAdvancedHelp

(0.002 seconds)

11—20 of 413 matching pages

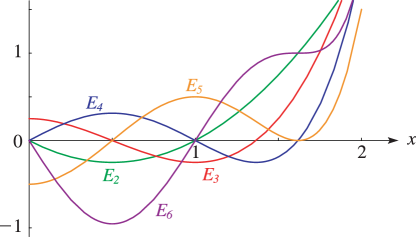
11: 24.3 Graphs

… ►

►►

Figure 24.3.2: Euler polynomials $E_n\left(x\right)$, $n=2,3,\mathrm{\dots },6$. Magnify

12: Bibliography

… ►

Tables of $\ln \mathrm{\Gamma }(z)$ for Complex Argument. Pergamon Press, New York.

ⓘ

External Links:

ZentralBlatt

Referenced by:

§5.22(iii).

Encodings:

BibTeX

… ►

Some determinants of Bernoulli, Euler and related numbers. Portugal. Math. 18, pp. 91–99.

ⓘ

External Links:

FullText, MathReview (D. P. Banerjee), ZentralBlatt

Referenced by:

§24.14(ii).

Encodings:

BibTeX

… ►

Algorithm 683: A portable FORTRAN subroutine for exponential integrals of a complex argument. ACM Trans. Math. Software 16 (2), pp. 178–182.

ⓘ

Notes:

Double- and single-precision Fortran, maximum accuracy 18S or 14S.

External Links:

ISSN 0098-3500, Document, GAMS (module 683; package TOMS), MathReview, ZentralBlatt

Referenced by:

1st item, 1st item.

Encodings:

BibTeX

… ►

A proof that Euler missed: Evaluating $\zeta (2)$ the easy way. Math. Intelligencer 5 (3), pp. 59–60.

ⓘ

External Links:

ISSN 0343-6993, MathReview (P. Szüsz), ZentralBlatt

Referenced by:

(25.6.7).

Encodings:

BibTeX

… ►

Numerical Tables for Angular Correlation Computations in $\alpha$-, $\beta$- and $\gamma$-Spectroscopy: $3j$-, $6j$-, $9j$-Symbols, F- and $\mathrm{\Gamma }$-Coefficients. Landolt-Börnstein Numerical Data and Functional Relationships in Science and Technology, Springer-Verlag.

ⓘ

External Links:

ISBN 978-3-540-04218-1

Referenced by:

§34.14.

Encodings:

BibTeX

…

13: 13.2 Definitions and Basic Properties

… ►The first two standard solutions are: … ►

13.2.4 $$M(a,b,z)=\mathrm{\Gamma }\left(b\right)𝐌(a,b,z).$$

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $M(a,b,z)$: $={}_1{}^{}F_1^{}(a;b;z)$ Kummer confluent hypergeometric function, $𝐌(a,b,z)$: Olver’s confluent hypergeometric function and $z$: complex variable

Referenced by:

§13.2(ii)

Permalink:

http://dlmf.nist.gov/13.2.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §13.2(i), §13.2(i), §13.2 and Ch.13

… ►

13.2.18 $$U(a,b,z)=\frac{\mathrm{\Gamma }\left(b-1\right)}{\mathrm{\Gamma }\left(a\right)}{z}^{1-b}+\frac{\mathrm{\Gamma }\left(1-b\right)}{\mathrm{\Gamma }\left(a-b+1\right)}+O\left(z^{2-\mathrm{\Re }b}\right),$$ , $b\ne 1$,

ⓘ

Symbols:

$O\left(x\right)$: order not exceeding, $\mathrm{\Gamma }\left(z\right)$: gamma function, $U(a,b,z)$: Kummer confluent hypergeometric function, $\mathrm{\Re }$: real part and $z$: complex variable

Permalink:

http://dlmf.nist.gov/13.2.E18

Encodings:

pMML, png, TeX

See also:

Annotations for §13.2(iii), §13.2 and Ch.13

►

13.2.19 $$U(a,1,z)=-\frac{1}{\mathrm{\Gamma }\left(a\right)}\left(\ln z+\psi \left(a\right)+2\gamma \right)+O\left(z\ln z\right),$$

ⓘ

Symbols:

$O\left(x\right)$: order not exceeding, $\mathrm{\Gamma }\left(z\right)$: gamma function, $\gamma$: Euler’s constant, $U(a,b,z)$: Kummer confluent hypergeometric function, $\psi \left(z\right)$: psi (or digamma) function, $\ln z$: principal branch of logarithm function and $z$: complex variable

A&S Ref:

13.5.9 (as corrected in later editions)

Referenced by:

§13.2(iii)

Permalink:

http://dlmf.nist.gov/13.2.E19

Encodings:

pMML, png, TeX

See also:

Annotations for §13.2(iii), §13.2 and Ch.13

… ►

13.2.42 $$U(a,b,z)=\frac{\mathrm{\Gamma }\left(1-b\right)}{\mathrm{\Gamma }\left(a-b+1\right)}M(a,b,z)+\frac{\mathrm{\Gamma }\left(b-1\right)}{\mathrm{\Gamma }\left(a\right)}{z}^{1-b}M(a-b+1,2-b,z).$$

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $M(a,b,z)$: $={}_1{}^{}F_1^{}(a;b;z)$ Kummer confluent hypergeometric function, $U(a,b,z)$: Kummer confluent hypergeometric function and $z$: complex variable

A&S Ref:

13.1.3 (in different form)

Referenced by:

§13.14(vii), §13.2(ii), §13.6(v), §13.9(ii), §33.13

Permalink:

http://dlmf.nist.gov/13.2.E42

Encodings:

pMML, png, TeX

See also:

Annotations for §13.2(vii), §13.2(vii), §13.2 and Ch.13

14: 4.19 Maclaurin Series and Laurent Series

§4.19 Maclaurin Series and Laurent Series

… ►In (4.19.3)–(4.19.9), $B_n$ are the Bernoulli numbers and $E_n$ are the Euler numbers (§§24.2(i)–24.2(ii)). … ►

4.19.5 $$\sec z=1+\frac{z^2}{2}+\frac{5}{24}{z}^4+\frac{61}{720}{z}^6+\mathrm{\cdots }+\frac{{(-1)}^n{E}_{2n}}{(2n)!}{z}^{2n}+\mathrm{\cdots },$$ ,

ⓘ

Symbols:

$E_n$: Euler numbers, $\pi$: the ratio of the circumference of a circle to its diameter, $!$: factorial (as in $n!$), $\sec z$: secant function, $n$: integer and $z$: complex variable

A&S Ref:

4.3.69

Referenced by:

§24.1, §24.19(i), §24.2(ii)

Permalink:

http://dlmf.nist.gov/4.19.E5

Encodings:

pMML, png, TeX

See also:

Annotations for §4.19 and Ch.4

…

15: Bibliography D

… ►

On the real roots of Euler polynomials. Monatsh. Math. 106 (2), pp. 115–138.

ⓘ

External Links:

ISSN 0026-9255, MathReview (H. M. Srivastava), ZentralBlatt

Referenced by:

§24.12(ii).

Encodings:

BibTeX

… ►

Asymptotic behaviour of Bernoulli, Euler, and generalized Bernoulli polynomials. J. Approx. Theory 49 (4), pp. 321–330.

ⓘ

External Links:

ISSN 0021-9045, Document, MathReview (Guillermo López Lagomasino), ZentralBlatt

Referenced by:

§24.11.

Encodings:

BibTeX

►

Irreducibility of certain generalized Bernoulli polynomials belonging to quadratic residue class characters. J. Number Theory 25 (1), pp. 72–80.

ⓘ

External Links:

ISSN 0022-314X, Document, MathReview (T. Metsänkylä)

Referenced by:

§24.12(iii).

Encodings:

BibTeX

►

Zeros of Bernoulli, generalized Bernoulli and Euler polynomials. Mem. Amer. Math. Soc. 73 (386), pp. iv+94.

ⓘ

External Links:

ISSN 0065-9266, MathReview (D. H. Lehmer), ZentralBlatt

Referenced by:

§24.12(i), §24.12(iii), §24.16(ii).

Encodings:

BibTeX

… ►

Error analysis in a uniform asymptotic expansion for the generalised exponential integral. J. Comput. Appl. Math. 80 (1), pp. 127–161.

ⓘ

External Links:

ISSN 0377-0427, Document, MathReview (Eberhard Wagner), ZentralBlatt

Referenced by:

§2.11(iii), §8.20(ii).

Encodings:

BibTeX

…

16: 16.15 Integral Representations and Integrals

… ►

16.15.1 $$F_1(\alpha ;\beta ,{\beta }^{\prime };\gamma ;x,y)=\frac{\mathrm{\Gamma }\left(\gamma \right)}{\mathrm{\Gamma }\left(\alpha \right)\mathrm{\Gamma }\left(\gamma -\alpha \right)}{\int }_0^1\frac{u^{\alpha -1}{(1-u)}^{\gamma -\alpha -1}}{{(1-ux)}^{\beta }{(1-uy)}^{{\beta }^{\prime }}}du,$$ $\mathrm{\Re }\alpha >0$, $\mathrm{\Re }\left(\gamma -\alpha \right)>0$,

ⓘ

Symbols:

$F_1(\alpha ;\beta ,{\beta }^{\prime };\gamma ;x,y)$: first Appell function, $\mathrm{\Gamma }\left(z\right)$: gamma function, $dx$: differential of $x$ , $\int$: integral and $\mathrm{\Re }$: real part

Keywords:

Mellin transform

Permalink:

http://dlmf.nist.gov/16.15.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §16.15 and Ch.16

►

16.15.2 $$F_2(\alpha ;\beta ,{\beta }^{\prime };\gamma ,{\gamma }^{\prime };x,y)=\frac{\mathrm{\Gamma }\left(\gamma \right)\mathrm{\Gamma }\left({\gamma }^{\prime }\right)}{\mathrm{\Gamma }\left(\beta \right)\mathrm{\Gamma }\left({\beta }^{\prime }\right)\mathrm{\Gamma }\left(\gamma -\beta \right)\mathrm{\Gamma }\left({\gamma }^{\prime }-{\beta }^{\prime }\right)}{\int }_0^1{\int }_0^1\frac{u^{\beta -1}{v}^{{\beta }^{\prime }-1}{(1-u)}^{\gamma -\beta -1}{(1-v)}^{{\gamma }^{\prime }-{\beta }^{\prime }-1}}{{(1-ux-vy)}^{\alpha }}dudv,$$ $\mathrm{\Re }\gamma >\mathrm{\Re }\beta >0$, $\mathrm{\Re }{\gamma }^{\prime }>\mathrm{\Re }{\beta }^{\prime }>0$,

ⓘ

Symbols:

$F_2(\alpha ;\beta ,{\beta }^{\prime };\gamma ,{\gamma }^{\prime };x,y)$: second Appell function, $\mathrm{\Gamma }\left(z\right)$: gamma function, $dx$: differential of $x$ , $\int$: integral and $\mathrm{\Re }$: real part

Keywords:

Mellin transform

Permalink:

http://dlmf.nist.gov/16.15.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §16.15 and Ch.16

►

16.15.3 $$F_3(\alpha ,{\alpha }^{\prime };\beta ,{\beta }^{\prime };\gamma ;x,y)=\frac{\mathrm{\Gamma }\left(\gamma \right)}{\mathrm{\Gamma }\left(\beta \right)\mathrm{\Gamma }\left({\beta }^{\prime }\right)\mathrm{\Gamma }\left(\gamma -\beta -{\beta }^{\prime }\right)}{\iint }_{\mathrm{\Delta }}\frac{u^{\beta -1}{v}^{{\beta }^{\prime }-1}{(1-u-v)}^{\gamma -\beta -{\beta }^{\prime }-1}}{{(1-ux)}^{\alpha }{(1-vy)}^{{\alpha }^{\prime }}}dudv,$$ $\mathrm{\Re }\left(\gamma -\beta -{\beta }^{\prime }\right)>0$, $\mathrm{\Re }\beta >0$, $\mathrm{\Re }{\beta }^{\prime }>0$,

ⓘ

Symbols:

$F_3(\alpha ,{\alpha }^{\prime };\beta ,{\beta }^{\prime };\gamma ;x,y)$: third Appell function, $\mathrm{\Gamma }\left(z\right)$: gamma function, $dx$: differential of $x$ and $\mathrm{\Re }$: real part

Keywords:

Mellin transform

Notes:

Erdélyi et al. (1953a, 5.8.1(3)) contains a typo.

Referenced by:

Erratum (V1.0.14) for Equation (16.15.3), Erratum (V1.0.14) for Equation (16.15.3)

Permalink:

http://dlmf.nist.gov/16.15.E3

Encodings:

pMML, png, TeX

Clarification (effective with 1.0.14):

A stray “$f$” was removed; it appeared after the comma at the end of this equation.

See also:

Annotations for §16.15 and Ch.16

… ►

16.15.4 $$F_4(\alpha ,\beta ;\gamma ,{\gamma }^{\prime };x(1-y),y(1-x))=\frac{\mathrm{\Gamma }\left(\gamma \right)\mathrm{\Gamma }\left({\gamma }^{\prime }\right)}{\mathrm{\Gamma }\left(\alpha \right)\mathrm{\Gamma }\left(\beta \right)\mathrm{\Gamma }\left(\gamma -\alpha \right)\mathrm{\Gamma }\left({\gamma }^{\prime }-\beta \right)}{\int }_0^1{\int }_0^1\frac{u^{\alpha -1}{v}^{\beta -1}{(1-u)}^{\gamma -\alpha -1}{(1-v)}^{{\gamma }^{\prime }-\beta -1}}{{(1-ux)}^{\gamma +{\gamma }^{\prime }-\alpha -1}{(1-vy)}^{\gamma +{\gamma }^{\prime }-\beta -1}{(1-ux-vy)}^{\alpha +\beta -\gamma -{\gamma }^{\prime }+1}}dudv,$$ $\mathrm{\Re }\gamma >\mathrm{\Re }\alpha >0$, $\mathrm{\Re }{\gamma }^{\prime }>\mathrm{\Re }\beta >0$.

ⓘ

Symbols:

$F_4(\alpha ,\beta ;\gamma ,{\gamma }^{\prime };x,y)$: fourth Appell function, $\mathrm{\Gamma }\left(z\right)$: gamma function, $dx$: differential of $x$ , $\int$: integral and $\mathrm{\Re }$: real part

Keywords:

Mellin transform

Source:

Burchnall and Chaundy (1940, (68))

Referenced by:

§16.15

Permalink:

http://dlmf.nist.gov/16.15.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §16.15 and Ch.16

…

17: 30.1 Special Notation

… ► ►►►

$x$	real variable. Except in §§30.7(iv), 30.11(ii), 30.13, and 30.14, .
${\gamma }^2$	real parameter (positive, zero, or negative).
…

►The main functions treated in this chapter are the eigenvalues ${\lambda }_n^m\left({\gamma }^2\right)$ and the spheroidal wave functions ${\mathrm{𝖯𝗌}}_n^m(x,{\gamma }^2)$, ${\mathrm{𝖰𝗌}}_n^m(x,{\gamma }^2)$, ${\mathrm{𝑃𝑠}}_n^m(z,{\gamma }^2)$, ${\mathrm{𝑄𝑠}}_n^m(z,{\gamma }^2)$, and $S_n^{m(j)}(z,\gamma )$, $j=1,2,3,4$. …Meixner and Schäfke (1954) use $\mathrm{ps}$, $\mathrm{qs}$, $\mathrm{Ps}$, $\mathrm{Qs}$ for $\mathrm{𝖯𝗌}$, $\mathrm{𝖰𝗌}$, $\mathrm{𝑃𝑠}$, $\mathrm{𝑄𝑠}$, respectively. … ►Flammer (1957) and Abramowitz and Stegun (1964) use ${\lambda }_{mn}(\gamma )$ for ${\lambda }_n^m\left({\gamma }^2\right)+{\gamma }^2$, $R_{mn}^{(j)}(\gamma ,z)$ for $S_n^{m(j)}(z,\gamma )$, and …where $d_{mn}(\gamma )$ is a normalization constant determined by …

18: 2.10 Sums and Sequences

… ►

§2.10(i) Euler–Maclaurin Formula

… ►This is the Euler–Maclaurin formula. … ►In both expansions the remainder term is bounded in absolute value by the first neglected term in the sum, and has the same sign, provided that in the case of (2.10.7), truncation takes place at $s=2m-1$, where $m$ is any positive integer satisfying $m\ge \frac{1}{2}(\alpha +1)$. ►For extensions of the Euler–Maclaurin formula to functions $f(x)$ with singularities at $x=a$ or $x=n$ (or both) see Sidi (2004, 2012b, 2012a). … ► …

19: 10.32 Integral Representations

… ►

10.32.2 $$I_{\nu }\left(z\right)=\frac{{(\frac{1}{2}z)}^{\nu }}{{\pi }^{\frac{1}{2}}\mathrm{\Gamma }\left(\nu +\frac{1}{2}\right)}{\int }_0^{\pi }{\mathrm{e}}^{\pm z\cos \theta }{(\sin \theta )}^{2\nu }d\theta =\frac{{(\frac{1}{2}z)}^{\nu }}{{\pi }^{\frac{1}{2}}\mathrm{\Gamma }\left(\nu +\frac{1}{2}\right)}{\int }_{-1}^1{(1-t^2)}^{\nu -\frac{1}{2}}{\mathrm{e}}^{\pm zt}dt,$$ $\mathrm{\Re }\nu >-\frac{1}{2}$.

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $\pi$: the ratio of the circumference of a circle to its diameter, $\cos z$: cosine function, $dx$: differential of $x$ , $\mathrm{e}$: base of natural logarithm, $\int$: integral, $I_{\nu }\left(z\right)$: modified Bessel function of the first kind, $\mathrm{\Re }$: real part, $\sin z$: sine function, $z$: complex variable and $\nu$: complex parameter

A&S Ref:

9.6.18

Permalink:

http://dlmf.nist.gov/10.32.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §10.32(i), §10.32 and Ch.10

… ►

10.32.5 $$K_0\left(z\right)=-\frac{1}{\pi }{\int }_0^{\pi }{\mathrm{e}}^{\pm z\cos \theta }\left(\gamma +\ln \left(2z{(\sin \theta )}^2\right)\right)d\theta .$$

ⓘ

Symbols:

$\gamma$: Euler’s constant, $\pi$: the ratio of the circumference of a circle to its diameter, $\cos z$: cosine function, $dx$: differential of $x$ , $\mathrm{e}$: base of natural logarithm, $\int$: integral, $K_{\nu }\left(z\right)$: modified Bessel function of the second kind, $\ln z$: principal branch of logarithm function, $\sin z$: sine function and $z$: complex variable

A&S Ref:

9.6.17

Permalink:

http://dlmf.nist.gov/10.32.E5

Encodings:

pMML, png, TeX

See also:

Annotations for §10.32(i), §10.32 and Ch.10

… ►

10.32.14 $$K_{\nu }\left(z\right)=\frac{1}{2{\pi }^2\mathrm{i}}{\left(\frac{\pi }{2z}\right)}^{\frac{1}{2}}{\mathrm{e}}^{-z}\cos \left(\nu \pi \right){\int }_{-\mathrm{i}\mathrm{\infty }}^{\mathrm{i}\mathrm{\infty }}\mathrm{\Gamma }\left(t\right)\mathrm{\Gamma }\left(\frac{1}{2}-t-\nu \right)\mathrm{\Gamma }\left(\frac{1}{2}-t+\nu \right){(2z)}^{t}dt,$$ .

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $\pi$: the ratio of the circumference of a circle to its diameter, $\cos z$: cosine function, $dx$: differential of $x$ , $\mathrm{e}$: base of natural logarithm, $\mathrm{i}$: imaginary unit, $\mathbb{Z}$: set of all integers, $\int$: integral, $K_{\nu }\left(z\right)$: modified Bessel function of the second kind, $\notin$: not an element of, $\mathrm{ph}$: phase, $z$: complex variable and $\nu$: complex parameter

Keywords:

Mellin transform

Referenced by:

§10.32(ii), §10.74(iii)

Permalink:

http://dlmf.nist.gov/10.32.E14

Encodings:

pMML, png, TeX

See also:

Annotations for §10.32(ii), §10.32(ii), §10.32 and Ch.10

►In (10.32.14) the integration contour separates the poles of $\mathrm{\Gamma }\left(t\right)$ from the poles of $\mathrm{\Gamma }\left(\frac{1}{2}-t-\nu \right)\mathrm{\Gamma }\left(\frac{1}{2}-t+\nu \right)$. … ►

10.32.19 $$K_{\mu }\left(z\right)K_{\nu }\left(z\right)=\frac{1}{8\pi \mathrm{i}}{\int }_{c-\mathrm{i}\mathrm{\infty }}^{c+\mathrm{i}\mathrm{\infty }}\frac{\mathrm{\Gamma }\left(t+\frac{1}{2}\mu +\frac{1}{2}\nu \right)\mathrm{\Gamma }\left(t+\frac{1}{2}\mu -\frac{1}{2}\nu \right)\mathrm{\Gamma }\left(t-\frac{1}{2}\mu +\frac{1}{2}\nu \right)\mathrm{\Gamma }\left(t-\frac{1}{2}\mu -\frac{1}{2}\nu \right)}{\mathrm{\Gamma }\left(2t\right)}{(\frac{1}{2}z)}^{-2t}dt,$$ .

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $\pi$: the ratio of the circumference of a circle to its diameter, $dx$: differential of $x$ , $\mathrm{i}$: imaginary unit, $\int$: integral, $K_{\nu }\left(z\right)$: modified Bessel function of the second kind, $\mathrm{ph}$: phase, $\mathrm{\Re }$: real part, $z$: complex variable and $\nu$: complex parameter

Keywords:

Mellin transform

Referenced by:

§10.32(iii)

Permalink:

http://dlmf.nist.gov/10.32.E19

Encodings:

pMML, png, TeX

See also:

Annotations for §10.32(iii), §10.32(iii), §10.32 and Ch.10

…

20: 15.2 Definitions and Analytical Properties

… ►

§15.2(i) Gauss Series

… ►

15.2.1 $$F(a,b;c;z)=\sum _{s=0}^{\mathrm{\infty }}\frac{{\left(a\right)}_s{\left(b\right)}_s}{{\left(c\right)}_{s}s!}{z}^s=1+\frac{ab}{c}z+\frac{a(a+1)b(b+1)}{c(c+1)2!}{z}^2+\mathrm{\cdots }=\frac{\mathrm{\Gamma }\left(c\right)}{\mathrm{\Gamma }\left(a\right)\mathrm{\Gamma }\left(b\right)}\sum _{s=0}^{\mathrm{\infty }}\frac{\mathrm{\Gamma }\left(a+s\right)\mathrm{\Gamma }\left(b+s\right)}{\mathrm{\Gamma }\left(c+s\right)s!}{z}^s,$$

ⓘ

Defines:

$F(a,b;c;z)$ or $F(\genfrac{}{}{0pt}{}{a,b}{c};z)$: $={}_2{}^{}F_1^{}(a,b;c;z)$ Gauss’ hypergeometric function

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, ${}_2{}^{}F_1^{}(a,b;c;z)$: $=F(a,b;c;z)$ notation for Gauss’ hypergeometric function, ${\left(a\right)}_n$: Pochhammer’s symbol (or shifted factorial), $!$: factorial (as in $n!$), $s$: nonnegative integer, $z$: complex variable, $a$: real or complex parameter, $b$: real or complex parameter and $c$: real or complex parameter

A&S Ref:

15.1.1

Referenced by:

§15.19(i), §15.4(iii), §18.30(v), §18.35(i), §18.35(ii), §19.19

Permalink:

http://dlmf.nist.gov/15.2.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §15.2(i), §15.2 and Ch.15

… ►

15.2.2 $$𝐅(a,b;c;z)=\sum _{s=0}^{\mathrm{\infty }}\frac{{\left(a\right)}_s{\left(b\right)}_s}{\mathrm{\Gamma }\left(c+s\right)s!}{z}^s,$$ ,

ⓘ

Defines:

$𝐅(a,b;c;z)$ or $𝐅(\genfrac{}{}{0pt}{}{a,b}{c};z)$: $={}_2{}^{}𝐅_1^{}(a,b;c;z)$ Olver’s hypergeometric function

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, ${\left(a\right)}_n$: Pochhammer’s symbol (or shifted factorial), $!$: factorial (as in $n!$), ${}_p{}^{}𝐅_q^{}(𝐚;𝐛;z)$ or ${}_p{}^{}𝐅_q^{}(\genfrac{}{}{0pt}{}{𝐚}{𝐛};z)$: scaled (or Olver’s) generalized hypergeometric function, $s$: nonnegative integer, $z$: complex variable, $a$: real or complex parameter, $b$: real or complex parameter and $c$: real or complex parameter

Referenced by:

§15.12(i), §16.2(v)

Permalink:

http://dlmf.nist.gov/15.2.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §15.2(i), §15.2 and Ch.15

… ►

15.2.3 $$𝐅(\genfrac{}{}{0pt}{}{a,b}{c};x+\mathrm{i}0)-𝐅(\genfrac{}{}{0pt}{}{a,b}{c};x-\mathrm{i}0)=\frac{2\pi \mathrm{i}}{\mathrm{\Gamma }\left(a\right)\mathrm{\Gamma }\left(b\right)}{(x-1)}^{c-a-b}𝐅(\genfrac{}{}{0pt}{}{c-a,c-b}{c-a-b+1};1-x),$$ $x>1$.

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{i}$: imaginary unit, $𝐅(a,b;c;z)$ or $𝐅(\genfrac{}{}{0pt}{}{a,b}{c};z)$: $={}_2{}^{}𝐅_1^{}(a,b;c;z)$ Olver’s hypergeometric function, $x$: real variable, $a$: real or complex parameter, $b$: real or complex parameter and $c$: real or complex parameter

Referenced by:

§15.2(i)

Permalink:

http://dlmf.nist.gov/15.2.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §15.2(i), §15.2 and Ch.15

… ►In that case we are using interpretation (15.2.6) since with interpretation (15.2.5) we would obtain that $F(-m,b;-m;z)$ is equal to the first $m+1$ terms of the Maclaurin series for ${(1-z)}^{-b}$.