30 Spheroidal Wave Functions Properties 30.10 Series and Integrals 30.12 Generalized and Coulomb Spheroidal Functions

§30.11 Radial Spheroidal Wave Functions

Keywords:: radial spheroidal wave functions, spheroidal wave functions
Permalink:: http://dlmf.nist.gov/30.11

§30.11(i) Definitions
§30.11(ii) Graphics
§30.11(iii) Asymptotic Behavior
§30.11(iv) Wronskian
§30.11(v) Connection with the $\mathop{\mathit{Ps}\/}\nolimits$ and $\mathop{\mathit{Qs}\/}\nolimits$ Functions
§30.11(vi) Integral Representations

§30.11(i) Definitions

Notes:: See Arscott (1964b, §8.5).
Keywords:: radial spheroidal wave functions
Permalink:: http://dlmf.nist.gov/30.11.i

Denote

30.11.1 $\psi_{k}^{{(j)}}(z)=\left(\frac{\pi}{2z}\right)^{{\frac{1}{2}}}{\cal C}_{{k+% \frac{1}{2}}}^{{(j)}}(z),$

Symbols:: : complex variable, $\psi_{k}^{{(j)}}(z)$ : spherical function and ${\cal C}_{\nu}^{{(j)}}$ : a Bessel function
A&S Ref:: 21.9.1 (in different form)
Permalink:: http://dlmf.nist.gov/30.11.E1
Encodings:: TeX, pMML, png

where

30.11.2

${\cal C}_{\nu}^{{(1)}}=\mathop{J_{{\nu}}\/}\nolimits,$

${\cal C}_{\nu}^{{(2)}}=\mathop{Y_{{\nu}}\/}\nolimits,$

${\cal C}_{\nu}^{{(3)}}=\mathop{{H^{{(1)}}_{{\nu}}}\/}\nolimits,$

${\cal C}_{\nu}^{{(4)}}=\mathop{{H^{{(2)}}_{{\nu}}}\/}\nolimits,$

Symbols:: $\mathop{J_{{\nu}}\/}\nolimits\!\left(z\right)$ : Bessel function of the first kind, $\mathop{Y_{{\nu}}\/}\nolimits\!\left(z\right)$ : Bessel function of the second kind, $\mathop{{H^{{(1)}}_{{\nu}}}\/}\nolimits\!\left(z\right)$ : Bessel function of the third kind (or Hankel function), $\mathop{{H^{{(2)}}_{{\nu}}}\/}\nolimits\!\left(z\right)$ : Bessel function of the third kind (or Hankel function) and ${\cal C}_{\nu}^{{(j)}}$ : a Bessel function
Permalink:: http://dlmf.nist.gov/30.11.E2
Encodings:: TeX, TeX, TeX, TeX, pMML, pMML, pMML, pMML, png, png, png, png

with $\mathop{J_{{\nu}}\/}\nolimits$ , $\mathop{Y_{{\nu}}\/}\nolimits$ , $\mathop{{H^{{(1)}}_{{\nu}}}\/}\nolimits$ , and $\mathop{{H^{{(2)}}_{{\nu}}}\/}\nolimits$ as in §10.2(ii). Then solutions of (30.2.1) with $\mu=m$ and $\lambda=\mathop{\lambda^{{m}}_{{n}}\/}\nolimits\!\left(\gamma^{2}\right)$ are given by

30.11.3 $\mathop{S^{{m(j)}}_{{n}}\/}\nolimits\!\left(z,\gamma\right)=\frac{(1-z^{{-2}})% ^{{\frac{1}{2}m}}}{A_{n}^{{-m}}(\gamma^{2})}\sum_{{2k\geq m-n}}a^{{-m}}_{{n,k}% }(\gamma^{2})\psi_{{n+2k}}^{{(j)}}(\gamma z).$

Defines:: $\mathop{S^{{m(j)}}_{{n}}\/}\nolimits\!\left(z,\gamma\right)$ : radial spheroidal wave function
Symbols:: : complex variable, : nonnegative integer, $n\geq m$ : integer degree, $\psi_{k}^{{(j)}}(z)$ : spherical function, $A_{n}^{m}(\gamma^{2})$ , $\gamma^{2}$ : real parameter and $a^{m}_{{n,k}}(\gamma^{2})$ : coefficients
A&S Ref:: 21.9.1 (in different form)
Referenced by:: §30.11(i), §30.16(iii)
Permalink:: http://dlmf.nist.gov/30.11.E3
Encodings:: TeX, pMML, png

Here $a^{{-m}}_{{n,k}}(\gamma^{2})$ is defined by (30.8.2) and (30.8.6), and

30.11.4 $A_{n}^{{\pm m}}(\gamma^{2})=\sum_{{2k\geq\mp m-n}}(-1)^{k}a^{{\pm m}}_{{n,k}}(% \gamma^{2})\quad(\neq 0).$

Symbols:: : nonnegative integer, $n\geq m$ : integer degree, $A_{n}^{m}(\gamma^{2})$ , $\gamma^{2}$ : real parameter and $a^{m}_{{n,k}}(\gamma^{2})$ : coefficients
Referenced by:: §30.5, ¶ ‣ §30.6
Permalink:: http://dlmf.nist.gov/30.11.E4
Encodings:: TeX, pMML, png

In (30.11.3) $z\neq 0$ when , and when .

¶ Connection Formulas

Keywords:: radial spheroidal wave functions

30.11.5

$\mathop{S^{{m(3)}}_{{n}}\/}\nolimits\!\left(z,\gamma\right)=\mathop{S^{{m(1)}}% _{{n}}\/}\nolimits\!\left(z,\gamma\right)+i\mathop{S^{{m(2)}}_{{n}}\/}% \nolimits\!\left(z,\gamma\right),$

$\mathop{S^{{m(4)}}_{{n}}\/}\nolimits\!\left(z,\gamma\right)=\mathop{S^{{m(1)}}% _{{n}}\/}\nolimits\!\left(z,\gamma\right)-i\mathop{S^{{m(2)}}_{{n}}\/}% \nolimits\!\left(z,\gamma\right).$

Symbols:: $\mathop{S^{{m(j)}}_{{n}}\/}\nolimits\!\left(z,\gamma\right)$ : radial spheroidal wave function, : complex variable, : nonnegative integer, $n\geq m$ : integer degree and $\gamma^{2}$ : real parameter
Permalink:: http://dlmf.nist.gov/30.11.E5
Encodings:: TeX, TeX, pMML, pMML, png, png

§30.11(ii) Graphics

Notes:: Figures 30.11.1–30.11.4 were produced at NIST with the aid of Maple procedures provided by the author.
Keywords:: radial spheroidal wave functions, spheroidal wave functions
Referenced by:: §30.1
Permalink:: http://dlmf.nist.gov/30.11.ii

Figure 30.11.1: $\mathop{S^{{0(1)}}_{{n}}\/}\nolimits\!\left(x,2\right)$ ,

, $1\leq x\leq 10$ .

Symbols:: $\mathop{S^{{m(j)}}_{{n}}\/}\nolimits\!\left(z,\gamma\right)$ : radial spheroidal wave function, : real variable and $n\geq m$ : integer degree
Referenced by:: §30.11(ii)
Permalink:: http://dlmf.nist.gov/30.11.F1
Encodings:: pdf, png

Figure 30.11.2: $\mathop{S^{{0(1)}}_{{n}}\/}\nolimits\!\left(iy,2i\right)$ ,

, $0\leq y\leq 10$ .

Symbols:: $\mathop{S^{{m(j)}}_{{n}}\/}\nolimits\!\left(z,\gamma\right)$ : radial spheroidal wave function, : real variable and $n\geq m$ : integer degree
Permalink:: http://dlmf.nist.gov/30.11.F2
Encodings:: pdf, png

Figure 30.11.3: $\mathop{S^{{1(1)}}_{{n}}\/}\nolimits\!\left(x,2\right)$ ,

, $1\leq x\leq 10$ .

Symbols:: $\mathop{S^{{m(j)}}_{{n}}\/}\nolimits\!\left(z,\gamma\right)$ : radial spheroidal wave function, : real variable and $n\geq m$ : integer degree
Permalink:: http://dlmf.nist.gov/30.11.F3
Encodings:: pdf, png

Figure 30.11.4: $\mathop{S^{{1(1)}}_{{n}}\/}\nolimits\!\left(iy,2i\right)$ ,

, $0\leq y\leq 10$ .

Symbols:: $\mathop{S^{{m(j)}}_{{n}}\/}\nolimits\!\left(z,\gamma\right)$ : radial spheroidal wave function, : real variable and $n\geq m$ : integer degree
Referenced by:: §30.11(ii)
Permalink:: http://dlmf.nist.gov/30.11.F4
Encodings:: pdf, png

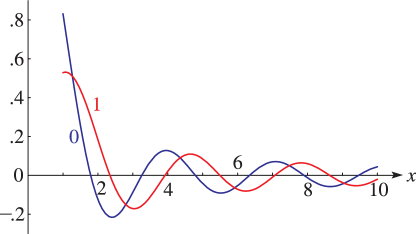
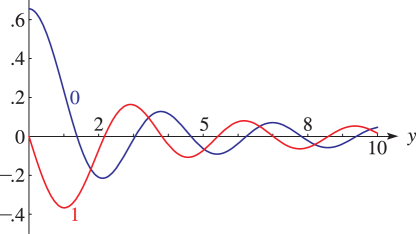
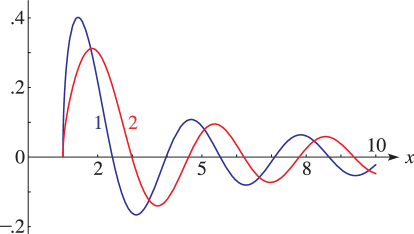
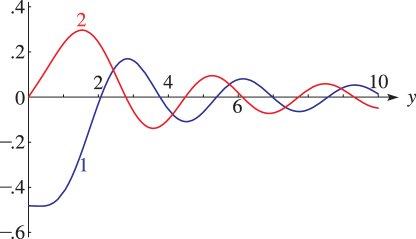
§30.11(iii) Asymptotic Behavior

Notes:: See Meixner and Schäfke (1954, §3.64).
Keywords:: radial spheroidal wave functions
Permalink:: http://dlmf.nist.gov/30.11.iii

For fixed $\gamma$ , as $z\to\infty$ in the sector $|\mathop{\mathrm{ph}\/}\nolimits z|\leq\pi-\delta$ ( $<\pi$ ),

30.11.6 $\mathop{S^{{m(j)}}_{{n}}\/}\nolimits\!\left(z,\gamma\right)=\begin{cases}\psi_% {n}^{{(j)}}(\gamma z)+\mathop{O\/}\nolimits\!\left(z^{{-2}}e^{{|\imagpart{z}|}% }\right),&j=1,2,\\ \psi_{n}^{{(j)}}(\gamma z)\left(1+\mathop{O\/}\nolimits\!\left(z^{{-1}}\right)% \right),&j=3,4.\end{cases}$

Symbols:: $\mathop{O\/}\nolimits\!\left(x\right)$ : order not exceeding, : base of exponential function, $\imagpart{}$ : imaginary part, $\mathop{S^{{m(j)}}_{{n}}\/}\nolimits\!\left(z,\gamma\right)$ : radial spheroidal wave function, : complex variable, : nonnegative integer, $n\geq m$ : integer degree, $\psi_{k}^{{(j)}}(z)$ : spherical function and $\gamma^{2}$ : real parameter
Permalink:: http://dlmf.nist.gov/30.11.E6
Encodings:: TeX, pMML, png

For asymptotic expansions in negative powers of see Meixner and Schäfke (1954, p. 293).

§30.11(iv) Wronskian

Notes:: See Meixner and Schäfke (1954, §3.65).
Keywords:: Wronskian, radial spheroidal wave functions
Permalink:: http://dlmf.nist.gov/30.11.iv

30.11.7 $\mathop{\mathscr{W}\/}\nolimits\left\{\mathop{S^{{m(1)}}_{{n}}\/}\nolimits\!% \left(z,\gamma\right),\mathop{S^{{m(2)}}_{{n}}\/}\nolimits\!\left(z,\gamma% \right)\right\}=\frac{1}{\gamma(z^{2}-1)}.$

Symbols:: $\mathop{\mathscr{W}\/}\nolimits$ : Wronskian, $\mathop{S^{{m(j)}}_{{n}}\/}\nolimits\!\left(z,\gamma\right)$ : radial spheroidal wave function, : complex variable, : nonnegative integer, $n\geq m$ : integer degree and $\gamma^{2}$ : real parameter
Permalink:: http://dlmf.nist.gov/30.11.E7
Encodings:: TeX, pMML, png

§30.11(v) Connection with the $\mathop{\mathit{Ps}\/}\nolimits$ and $\mathop{\mathit{Qs}\/}\nolimits$ Functions

Notes:: See Erdélyi et al. (1955, §16.11) and Meixner and Schäfke (1954, §3.66).
Keywords:: radial spheroidal wave functions
Referenced by:: §30.15(i), §30.18(i)
Permalink:: http://dlmf.nist.gov/30.11.v

30.11.8 $\mathop{S^{{m(1)}}_{{n}}\/}\nolimits\!\left(z,\gamma\right)=K_{n}^{m}(\gamma)% \mathop{\mathit{Ps}^{{m}}_{{n}}\/}\nolimits\!\left(z,\gamma^{2}\right),$

Symbols:: $\mathop{S^{{m(j)}}_{{n}}\/}\nolimits\!\left(z,\gamma\right)$ : radial spheroidal wave function, $\mathop{\mathit{Ps}^{{m}}_{{n}}\/}\nolimits\!\left(z,\gamma^{2}\right)$ : spheroidal wave function of complex argument, : complex variable, : nonnegative integer, $n\geq m$ : integer degree, $K_{n}^{m}(\gamma)$ : connection coefficient and $\gamma^{2}$ : real parameter
A&S Ref:: 21.10.1 (in different form)
Permalink:: http://dlmf.nist.gov/30.11.E8
Encodings:: TeX, pMML, png

30.11.9 $\mathop{S^{{m(2)}}_{{n}}\/}\nolimits\!\left(z,\gamma\right)=\frac{(n-m)!}{(n+m% )!}\frac{(-1)^{{m+1}}\mathop{\mathit{Qs}^{{m}}_{{n}}\/}\nolimits\!\left(z,% \gamma^{2}\right)}{\gamma K_{n}^{m}(\gamma)A_{n}^{m}(\gamma^{2})A_{n}^{{-m}}(% \gamma^{2})},$

Symbols:: : : factorial, $\mathop{S^{{m(j)}}_{{n}}\/}\nolimits\!\left(z,\gamma\right)$ : radial spheroidal wave function, $\mathop{\mathit{Qs}^{{m}}_{{n}}\/}\nolimits\!\left(z,\gamma^{2}\right)$ : spheroidal wave function of complex argument, : complex variable, : nonnegative integer, $n\geq m$ : integer degree, $A_{n}^{m}(\gamma^{2})$ , $K_{n}^{m}(\gamma)$ : connection coefficient and $\gamma^{2}$ : real parameter
A&S Ref:: 21.10.2 (in different form)
Permalink:: http://dlmf.nist.gov/30.11.E9
Encodings:: TeX, pMML, png

where

30.11.10 $K_{n}^{m}(\gamma)=\frac{\sqrt{\pi}}{2}\left(\frac{\gamma}{2}\right)^{m}\frac{(% -1)^{m}a_{{n,\frac{1}{2}(m-n)}}^{{-m}}(\gamma^{2})}{\mathop{\Gamma\/}\nolimits% \!\left(\frac{3}{2}+m\right)A_{n}^{{-m}}(\gamma^{2})\mathop{\mathsf{Ps}^{{m}}_% {{n}}\/}\nolimits\!\left(0,\gamma^{2}\right)},$

even,

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, $\mathop{\mathsf{Ps}^{{m}}_{{n}}\/}\nolimits\!\left(x,\gamma^{2}\right)$ : spheroidal wave function of the first kind, : nonnegative integer, $n\geq m$ : integer degree, $A_{n}^{m}(\gamma^{2})$ , $K_{n}^{m}(\gamma)$ : connection coefficient, $\gamma^{2}$ : real parameter and $a^{m}_{{n,k}}(\gamma^{2})$ : coefficients
Referenced by:: §30.16(iii)
Permalink:: http://dlmf.nist.gov/30.11.E10
Encodings:: TeX, pMML, png

30.11.11 $K_{n}^{m}(\gamma)=\frac{\sqrt{\pi}}{2}\left(\frac{\gamma}{2}\right)^{{m+1}}\*% \frac{(-1)^{m}a_{{n,\frac{1}{2}(m-n+1)}}^{{-m}}(\gamma^{2})}{\mathop{\Gamma\/}% \nolimits\!\left(\frac{5}{2}+m\right)A_{n}^{{-m}}(\gamma^{2})(\left.\ifrac{d% \mathop{\mathsf{Ps}^{{m}}_{{n}}\/}\nolimits(z,\gamma^{2})}{dz}\right|_{{z=0}})},$

odd.

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, $\frac{df}{dx}$ : derivative of with respect to , $\mathop{\mathsf{Ps}^{{m}}_{{n}}\/}\nolimits\!\left(x,\gamma^{2}\right)$ : spheroidal wave function of the first kind, : complex variable, : nonnegative integer, $n\geq m$ : integer degree, $A_{n}^{m}(\gamma^{2})$ , $K_{n}^{m}(\gamma)$ : connection coefficient, $\gamma^{2}$ : real parameter and $a^{m}_{{n,k}}(\gamma^{2})$ : coefficients
Referenced by:: §30.16(iii)
Permalink:: http://dlmf.nist.gov/30.11.E11
Encodings:: TeX, pMML, png

§30.11(vi) Integral Representations

Notes:: See Meixner and Schäfke (1954, §3.84).
Keywords:: radial spheroidal wave functions
Permalink:: http://dlmf.nist.gov/30.11.vi

When $z\in\Complex\setminus(-\infty,1]$

30.11.12 $A_{n}^{{-m}}(\gamma^{2})\mathop{S^{{m(1)}}_{{n}}\/}\nolimits\!\left(z,\gamma% \right)=\frac{1}{2}i^{{m+n}}\gamma^{m}\frac{(n-m)!}{(n+m)!}z^{m}(1-z^{{-2}})^{% {\frac{1}{2}m}}\*\int_{{-1}}^{1}e^{{-i\gamma zt}}(1-t^{2})^{{\frac{1}{2}m}}% \mathop{\mathsf{Ps}^{{m}}_{{n}}\/}\nolimits\!\left(t,\gamma^{2}\right)dt.$

Symbols:: : differential of , : base of exponential function, : : factorial, $\int$ : integral, $\mathop{S^{{m(j)}}_{{n}}\/}\nolimits\!\left(z,\gamma\right)$ : radial spheroidal wave function, $\mathop{\mathsf{Ps}^{{m}}_{{n}}\/}\nolimits\!\left(x,\gamma^{2}\right)$ : spheroidal wave function of the first kind, : complex variable, : nonnegative integer, $n\geq m$ : integer degree, $A_{n}^{m}(\gamma^{2})$ and $\gamma^{2}$ : real parameter
Permalink:: http://dlmf.nist.gov/30.11.E12
Encodings:: TeX, pMML, png

For further relations see Arscott (1964b, §8.6), Connett et al. (1993), Erdélyi et al. (1955, §16.13), Meixner and Schäfke (1954), and Meixner et al. (1980, §3.1).

© 2010–2013 NIST / Privacy Policy / Disclaimer / Feedback; Version 1.0.6; Release date 2013-05-06 Math-Image version (See MathML) . A Printed Companionis available. 30.10 Series and Integrals 30.12 Generalized and Coulomb Spheroidal Functions