Bernoulli%20monosplines

SearchAdvancedHelp

(0.002 seconds)

1—10 of 144 matching pages

1: 24.1 Special Notation

… ►

Bernoulli Numbers and Polynomials

►The origin of the notation $B_n$, $B_n\left(x\right)$, is not clear. …

2: 24.17 Mathematical Applications

… ►The functions … ►

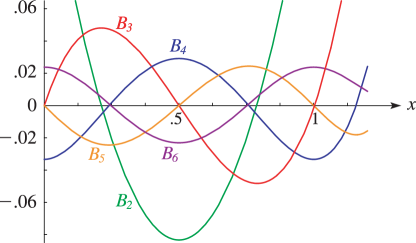
Bernoulli Monosplines

… ► $M_n(x)$ is a monospline of degree $n$, and it follows from (24.4.25) and (24.4.27) that … ► … ►

3: 24.2 Definitions and Generating Functions

§24.2 Definitions and Generating Functions

►

§24.2(i) Bernoulli Numbers and Polynomials

… ►

§24.2(iii) Periodic Bernoulli and Euler Functions

… ►

Table 24.2.1: Bernoulli and Euler numbers.

► ►►

$n$	$B_n$	$E_n$
…

►

…

4: 24.18 Physical Applications

§24.18 Physical Applications

►Bernoulli polynomials appear in statistical physics (Ordóñez and Driebe (1996)), in discussions of Casimir forces (Li et al. (1991)), and in a study of quark-gluon plasma (Meisinger et al. (2002)). …

5: 24.20 Tables

§24.20 Tables

… ►Wagstaff (1978) gives complete prime factorizations of $N_n$ and $E_n$ for $n=20(2)60$ and $n=8(2)42$, respectively. …

6: 24.3 Graphs

… ►

►►

Figure 24.3.1: Bernoulli polynomials $B_n\left(x\right)$, $n=2,3,\mathrm{\dots },6$. Magnify

…

7: 25.11 Hurwitz Zeta Function

… ►

25.11.6 $$\zeta (s,a)=\frac{1}{a^s}\left(\frac{1}{2}+\frac{a}{s-1}\right)-\frac{s(s+1)}{2}{\int }_0^{\mathrm{\infty }}\frac{{\tilde{B}}_2\left(x\right)-B_2}{{(x+a)}^{s+2}}dx,$$ $s\ne 1$, $\mathrm{\Re }s>-1$, $a>0$.

ⓘ

Symbols:

$B_n$: Bernoulli numbers, $\zeta (s,a)$: Hurwitz zeta function, $dx$: differential of $x$ , $\int$: integral, ${\tilde{B}}_n\left(x\right)$: periodic Bernoulli functions, $\mathrm{\Re }$: real part, $x$: real variable, $a$: real or complex parameter and $s$: complex variable

Keywords:

Euler–Maclaurin formula, improper integral

Source:

Apostol (1985a, (25), p. 231)

Referenced by:

Erratum (V1.0.12) for Equations (25.11.6), (25.11.19), and (25.11.20)

Permalink:

http://dlmf.nist.gov/25.11.E6

Encodings:

pMML, png, TeX

Errata (effective with 1.0.12):

Originally the integrand was incorrect because its numerator contained the function ${\tilde{B}}_2\left(x\right)$. The correct function is $\frac{{\tilde{B}}_2\left(x\right)-B_2}{2}$.

Reported 2016-05-08 by Clemens Heuberger

See also:

Annotations for §25.11(iii), §25.11 and Ch.25

… ►For ${\tilde{B}}_n\left(x\right)$ see §24.2(iii). … ►

25.11.14 $$\zeta (-n,a)=-\frac{B_{n+1}\left(a\right)}{n+1},$$ $n=0,1,2,\mathrm{\dots }$.

ⓘ

Symbols:

$B_n\left(x\right)$: Bernoulli polynomials, $\zeta (s,a)$: Hurwitz zeta function, $n$: nonnegative integer and $a$: real or complex parameter

Keywords:

special value

Source:

Apostol (1976, (17), p. 264)

Permalink:

http://dlmf.nist.gov/25.11.E14

Encodings:

pMML, png, TeX

See also:

Annotations for §25.11(v), §25.11 and Ch.25

… ►

25.11.19 $${\zeta }^{\prime }(s,a)=-\frac{\ln a}{a^s}\left(\frac{1}{2}+\frac{a}{s-1}\right)-\frac{a^{1-s}}{{(s-1)}^2}+\frac{s(s+1)}{2}{\int }_0^{\mathrm{\infty }}\frac{({\tilde{B}}_2\left(x\right)-B_2)\ln \left(x+a\right)}{{(x+a)}^{s+2}}dx-\frac{(2s+1)}{2}{\int }_0^{\mathrm{\infty }}\frac{{\tilde{B}}_2\left(x\right)-B_2}{{(x+a)}^{s+2}}dx,$$ $\mathrm{\Re }s>-1$, $s\ne 1$, $a>0$.

ⓘ

Symbols:

$B_n$: Bernoulli numbers, $\zeta (s,a)$: Hurwitz zeta function, $dx$: differential of $x$ , $\int$: integral, $\ln z$: principal branch of logarithm function, ${\tilde{B}}_n\left(x\right)$: periodic Bernoulli functions, $\mathrm{\Re }$: real part, $x$: real variable, $a$: real or complex parameter, $s$: complex variable and $k$: integer

Keywords:

derivative

Source:

Apostol (1985a, fourth equation, p. 231); with $k=1$, ${\phi }_2(x)=\frac{1}{2}({\tilde{B}}_2\left(x\right)-B_2)$

Referenced by:

Erratum (V1.0.12) for Equations (25.11.6), (25.11.19), and (25.11.20)

Permalink:

http://dlmf.nist.gov/25.11.E19

Encodings:

pMML, png, TeX

Errata (effective with 1.0.12):

Originally both integrands were incorrect because their numerators contained the function ${\tilde{B}}_2\left(x\right)$. The correct function is $\frac{{\tilde{B}}_2\left(x\right)-B_2}{2}$.

Reported 2016-06-27 by Gergő Nemes

See also:

Annotations for §25.11(vi), §25.11(vi), §25.11 and Ch.25

… ►

25.11.34 $$n{\int }_0^a{\zeta }^{\prime }(1-n,x)dx={\zeta }^{\prime }(-n,a)-{\zeta }^{\prime }\left(-n\right)+\frac{B_{n+1}-B_{n+1}\left(a\right)}{n(n+1)},$$ $n=1,2,\mathrm{\dots }$, $\mathrm{\Re }a>0$.

ⓘ

Symbols:

$B_n$: Bernoulli numbers, $B_n\left(x\right)$: Bernoulli polynomials, $\zeta (s,a)$: Hurwitz zeta function, $\zeta \left(s\right)$: Riemann zeta function, $dx$: differential of $x$ , $\int$: integral, $\mathrm{\Re }$: real part, $n$: nonnegative integer, $x$: real variable and $a$: real or complex parameter

Keywords:

definite integral, integral representation

Source:

Adamchik (1998, (15), p. 196)

Permalink:

http://dlmf.nist.gov/25.11.E34

Encodings:

pMML, png, TeX

See also:

Annotations for §25.11(viii), §25.11 and Ch.25

…

8: 5.11 Asymptotic Expansions

… ►For the Bernoulli numbers $B_{2k}$, see §24.2(i). … ►Wrench (1968) gives exact values of $g_k$ up to $g_{20}$. … ►where $h(\in ℂ)$ is fixed, and $B_k\left(h\right)$ is the Bernoulli polynomial defined in §24.2(i). … ►In terms of generalized Bernoulli polynomials $B_n^{(\mathrm{\ell })}\left(x\right)$ (§24.16(i)), we have for $k=0,1,\mathrm{\dots }$, ►

5.11.17 $$G_k(a,b)=\left(\genfrac{}{}{0.0pt}{}{a-b}{k}\right)B_k^{(a-b+1)}\left(a\right),$$

ⓘ

Defines:

$G_k(a,b)$: coefficients (locally)

Symbols:

$\left(\genfrac{}{}{0.0pt}{}{m}{n}\right)$: binomial coefficient, $B_n^{(\mathrm{\ell })}\left(x\right)$: generalized Bernoulli polynomials, $k$: nonnegative integer, $a$: real or complex variable and $b$: real or complex variable

Permalink:

http://dlmf.nist.gov/5.11.E17

Encodings:

pMML, png, TeX

See also:

Annotations for §5.11(iii), §5.11 and Ch.5

…

9: 24.4 Basic Properties

… ►

§24.4(ii) Symmetry

… ►

§24.4(v) Multiplication Formulas

►

Raabe’s Theorem

… ►

§24.4(vii) Derivatives

… ►

§24.4(ix) Relations to Other Functions

…

10: 24.16 Generalizations

§24.16 Generalizations

… ►

Bernoulli Numbers of the Second Kind

… ►

Degenerate Bernoulli Numbers

… ►

§24.16(ii) Character Analogs

… ►

§24.16(iii) Other Generalizations

…