7 Error Functions, Dawson’s and Fresnel Integrals Properties 7.18 Repeated Integrals of the Complementary Error Function 7.20 Mathematical Applications

§7.19 Voigt Functions

Permalink:: http://dlmf.nist.gov/7.19

§7.19(i) Definitions
§7.19(ii) Graphics
§7.19(iii) Properties
§7.19(iv) Other Integral Representations

§7.19(i) Definitions

Notes:: (7.19.3) follows from (7.2.3) and (7.7.2).
Keywords:: Voigt functions, error functions, line broadening function
Permalink:: http://dlmf.nist.gov/7.19.i

For $x\in\Real$ and ,

7.19.1 $\mathop{\mathsf{U}\/}\nolimits\!\left(x,t\right)=\frac{1}{\sqrt{4\pi t}}\int_{% {-\infty}}^{\infty}\frac{e^{{-(x-y)^{2}/(4t)}}}{1+y^{2}}dy,$

Defines:: $\mathop{\mathsf{U}\/}\nolimits\!\left(x,t\right)$ : Voigt function
Symbols:: : differential of , : base of exponential function, $\int$ : integral and : real variable
Referenced by:: §7.19(iii)
Permalink:: http://dlmf.nist.gov/7.19.E1
Encodings:: TeX, pMML, png

7.19.2 $\mathop{\mathsf{V}\/}\nolimits\!\left(x,t\right)=\frac{1}{\sqrt{4\pi t}}\int_{% {-\infty}}^{\infty}\frac{ye^{{-(x-y)^{2}/(4t)}}}{1+y^{2}}dy.$

Defines:: $\mathop{\mathsf{V}\/}\nolimits\!\left(x,t\right)$ : Voigt function
Symbols:: : differential of , : base of exponential function, $\int$ : integral and : real variable
Referenced by:: §7.19(iii)
Permalink:: http://dlmf.nist.gov/7.19.E2
Encodings:: TeX, pMML, png

7.19.3 $\mathop{\mathsf{U}\/}\nolimits\!\left(x,t\right)+i\mathop{\mathsf{V}\/}% \nolimits\!\left(x,t\right)=\sqrt{\frac{\pi}{4t}}e^{{z^{2}}}\mathop{\mathrm{% erfc}\/}\nolimits z,$ $z=(1-ix)/(2\sqrt{t})$ .

Symbols:: $\mathop{\mathsf{U}\/}\nolimits\!\left(x,t\right)$ : Voigt function, $\mathop{\mathsf{V}\/}\nolimits\!\left(x,t\right)$ : Voigt function, $\mathop{\mathrm{erfc}\/}\nolimits z$ : complementary error function, : base of exponential function, : real variable and : complex variable
Referenced by:: §7.19(i), §7.22(iv)
Permalink:: http://dlmf.nist.gov/7.19.E3
Encodings:: TeX, pMML, png

7.19.4 $\mathop{H\/}\nolimits\!\left(a,u\right)=\frac{a}{\pi}\int_{{-\infty}}^{\infty}% \frac{e^{{-t^{2}}}dt}{(u-t)^{2}+a^{2}}=\frac{1}{a\sqrt{\pi}}\mathop{\mathsf{U}% \/}\nolimits\!\left(\frac{u}{a},\frac{1}{4a^{2}}\right).$

Defines:: $\mathop{H\/}\nolimits\!\left(a,u\right)$ : line-broadening function
Symbols:: $\mathop{\mathsf{U}\/}\nolimits\!\left(x,t\right)$ : Voigt function, : differential of , : base of exponential function and $\int$ : integral
Permalink:: http://dlmf.nist.gov/7.19.E4
Encodings:: TeX, pMML, png

$\mathop{H\/}\nolimits\!\left(a,u\right)$ is sometimes called the line broadening function; see, for example, Finn and Mugglestone (1965).

§7.19(ii) Graphics

Notes:: These graphs were produced at NIST.
Permalink:: http://dlmf.nist.gov/7.19.ii

Figure 7.19.1: Voigt function $\mathop{\mathsf{U}\/}\nolimits\!\left(x,t\right)$ ,

, 2.5, 5, 10.

Symbols:: $\mathop{\mathsf{U}\/}\nolimits\!\left(x,t\right)$ : Voigt function and : real variable
Keywords:: Voigt functions
Permalink:: http://dlmf.nist.gov/7.19.F1
Encodings:: pdf, png

Figure 7.19.2: Voigt function $\mathop{\mathsf{V}\/}\nolimits\!\left(x,t\right)$ ,

, 2.5, 5, 10.

Symbols:: $\mathop{\mathsf{V}\/}\nolimits\!\left(x,t\right)$ : Voigt function and : real variable
Keywords:: Voigt functions
Permalink:: http://dlmf.nist.gov/7.19.F2
Encodings:: pdf, png

§7.19(iii) Properties

Notes:: (7.19.5) follows from the definitions (7.19.1), (7.19.2), together with (1.17.6) or §2.3(iii). For the first of (7.19.7) use (7.19.1) for the lower bound, and (7.19.10) for the upper bound. For the second of (7.19.7) use (7.19.11). For (7.19.8) and (7.19.9) again use the definitions (7.19.1) and (7.19.2).
Keywords:: Voigt functions
Permalink:: http://dlmf.nist.gov/7.19.iii

7.19.5

$\lim_{{t\to 0}}\mathop{\mathsf{U}\/}\nolimits\!\left(x,t\right)=\frac{1}{1+x^{% 2}},$

$\lim_{{t\to 0}}\mathop{\mathsf{V}\/}\nolimits\!\left(x,t\right)=\frac{x}{1+x^{% 2}}.$

Symbols:: $\mathop{\mathsf{U}\/}\nolimits\!\left(x,t\right)$ : Voigt function, $\mathop{\mathsf{V}\/}\nolimits\!\left(x,t\right)$ : Voigt function and : real variable
Referenced by:: §7.19(iii)
Permalink:: http://dlmf.nist.gov/7.19.E5
Encodings:: TeX, TeX, pMML, pMML, png, png

7.19.6

$\mathop{\mathsf{U}\/}\nolimits\!\left(-x,t\right)=\mathop{\mathsf{U}\/}% \nolimits\!\left(x,t\right),$

$\mathop{\mathsf{V}\/}\nolimits\!\left(-x,t\right)=-\mathop{\mathsf{V}\/}% \nolimits\!\left(x,t\right).$

Symbols:: $\mathop{\mathsf{U}\/}\nolimits\!\left(x,t\right)$ : Voigt function, $\mathop{\mathsf{V}\/}\nolimits\!\left(x,t\right)$ : Voigt function and : real variable
Permalink:: http://dlmf.nist.gov/7.19.E6
Encodings:: TeX, TeX, pMML, pMML, png, png

7.19.7

$0<\mathop{\mathsf{U}\/}\nolimits\!\left(x,t\right)\leq 1,$

$-1\leq\mathop{\mathsf{V}\/}\nolimits\!\left(x,t\right)\leq 1.$

Symbols:: $\mathop{\mathsf{U}\/}\nolimits\!\left(x,t\right)$ : Voigt function, $\mathop{\mathsf{V}\/}\nolimits\!\left(x,t\right)$ : Voigt function and : real variable
Referenced by:: §7.19(iii)
Permalink:: http://dlmf.nist.gov/7.19.E7
Encodings:: TeX, TeX, pMML, pMML, png, png

7.19.8 $\mathop{\mathsf{V}\/}\nolimits\!\left(x,t\right)=x\mathop{\mathsf{U}\/}% \nolimits\!\left(x,t\right)+2t\frac{\partial\mathop{\mathsf{U}\/}\nolimits\!% \left(x,t\right)}{\partial x},$

Symbols:: $\mathop{\mathsf{U}\/}\nolimits\!\left(x,t\right)$ : Voigt function, $\mathop{\mathsf{V}\/}\nolimits\!\left(x,t\right)$ : Voigt function, $\frac{\partial f}{\partial x}$ : partial derivative of with respect to and : real variable
Referenced by:: §7.19(iii)
Permalink:: http://dlmf.nist.gov/7.19.E8
Encodings:: TeX, pMML, png

7.19.9 $\mathop{\mathsf{U}\/}\nolimits\!\left(x,t\right)=1-x\mathop{\mathsf{V}\/}% \nolimits\!\left(x,t\right)-2t\frac{\partial\mathop{\mathsf{V}\/}\nolimits\!% \left(x,t\right)}{\partial x}.$

Symbols:: $\mathop{\mathsf{U}\/}\nolimits\!\left(x,t\right)$ : Voigt function, $\mathop{\mathsf{V}\/}\nolimits\!\left(x,t\right)$ : Voigt function, $\frac{\partial f}{\partial x}$ : partial derivative of with respect to and : real variable
Referenced by:: §7.19(iii)
Permalink:: http://dlmf.nist.gov/7.19.E9
Encodings:: TeX, pMML, png

§7.19(iv) Other Integral Representations

Notes:: See Armstrong (1967).
Permalink:: http://dlmf.nist.gov/7.19.iv

7.19.10 $\mathop{\mathsf{U}\/}\nolimits\!\left(\frac{u}{a},\frac{1}{4a^{2}}\right)=a% \int_{0}^{{\infty}}e^{{-at-\frac{1}{4}t^{2}}}\mathop{\cos\/}\nolimits\!\left(% ut\right)dt,$

Symbols:: $\mathop{\mathsf{U}\/}\nolimits\!\left(x,t\right)$ : Voigt function, $\mathop{\cos\/}\nolimits z$ : cosine function, : differential of , : base of exponential function and $\int$ : integral
Referenced by:: §7.19(iii)
Permalink:: http://dlmf.nist.gov/7.19.E10
Encodings:: TeX, pMML, png

7.19.11 $\mathop{\mathsf{V}\/}\nolimits\!\left(\frac{u}{a},\frac{1}{4a^{2}}\right)=a% \int_{0}^{{\infty}}e^{{-at-\frac{1}{4}t^{2}}}\mathop{\sin\/}\nolimits\!\left(% ut\right)dt.$

Symbols:: $\mathop{\mathsf{V}\/}\nolimits\!\left(x,t\right)$ : Voigt function, : differential of , : base of exponential function, $\int$ : integral and $\mathop{\sin\/}\nolimits z$ : sine function
Referenced by:: §7.19(iii)
Permalink:: http://dlmf.nist.gov/7.19.E11
Encodings:: TeX, pMML, png

© 2010–2013 NIST / Privacy Policy / Disclaimer / Feedback; Version 1.0.6; Release date 2013-05-06 Math-Image version (See MathML) . A Printed Companionis available. 7.18 Repeated Integrals of the Complementary Error Function 7.20 Mathematical Applications

§7.19 Voigt Functions

Contents

§7.19(i) Definitions

§7.19(ii) Graphics

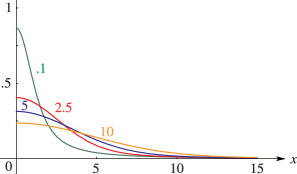
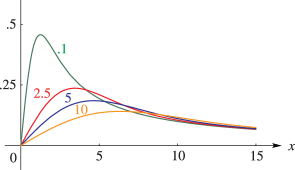
§7.19(iii) Properties

§7.19(iv) Other Integral Representations