Voigt functions

SearchAdvancedHelp

(0.002 seconds)

1—10 of 11 matching pages

1: 7.19 Voigt Functions

§7.19 Voigt Functions

►

§7.19(i) Definitions

… ►

►►

Figure 7.19.1: Voigt function $𝖴(x,t)$, $t=0.1$, $2.5$, $5$, $10$. Magnify

►

►►

Figure 7.19.2: Voigt function $𝖵(x,t)$, $t=0.1$, $2.5$, $5$, $10$. Magnify

►

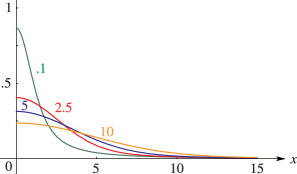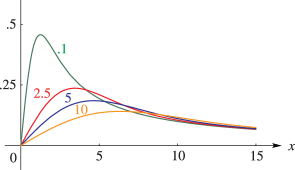§7.19(iii) Properties

…

2: 7.21 Physical Applications

… ►Voigt functions $𝖴(x,t)$, $𝖵(x,t)$, can be regarded as the convolution of a Gaussian and a Lorentzian, and appear when the analysis of light (or particulate) absorption (or emission) involves thermal motion effects. …

3: 7.22 Methods of Computation

… ►

§7.22(iv) Voigt Functions

…

4: 7.23 Tables

… ►

Abramowitz and Stegun (1964, Table 27.6) includes the Goodwin–Staton integral $G\left(x\right)$, $x=1(.1)3(.5)8$, 4D; also $G\left(x\right)+\ln x$, $x=0(.05)1$, 4D.

►

Finn and Mugglestone (1965) includes the Voigt function $H(a,u)$, $u\in [0,22]$, $a\in [0,1]$, 6S.

…

5: 7.1 Special Notation

… ►The main functions treated in this chapter are the error function $\mathrm{erf}z$; the complementary error functions $\mathrm{erfc}z$ and $w\left(z\right)$; Dawson’s integral $F\left(z\right)$; the Fresnel integrals $ℱ\left(z\right)$, $C\left(z\right)$, and $S\left(z\right)$; the Goodwin–Staton integral $G\left(z\right)$; the repeated integrals of the complementary error function ${\mathrm{i}}^n\mathrm{erfc}\left(z\right)$; the Voigt functions $𝖴(x,t)$ and $𝖵(x,t)$. …

6: Bibliography Z

… ►

Algorithm 916: computing the Faddeyeva and Voigt functions. ACM Trans. Math. Software 38 (2), pp. Art. 15, 22.

ⓘ

External Links:

ISSN 0098-3500, Document, FullText, MathReview Entry

Referenced by:

2nd item, 5th item.

Encodings:

BibTeX

►

Remark on “Algorithm 916: computing the Faddeyeva and Voigt functions”: efficiency improvements and Fortran translation. ACM Trans. Math. Softw. 42 (3), pp. 26:1–26:9.

ⓘ

Notes:

Includes MATLAB and Fortran programs claiming 6S or 13S accuracy for single and double precision

External Links:

ISSN 0098-3500, Link, Document, MathReview Entry

Referenced by:

3rd item, 6th item, §7.25(iii), §7.25(vi).

Encodings:

BibTeX

…

7: Bibliography

… ►

Spectrum line profiles: The Voigt function. J. Quant. Spectrosc. Radiat. Transfer 7, pp. 61–88.

ⓘ

External Links:

Document

Referenced by:

§7.19(iv), §7.21.

Encodings:

BibTeX

…

8: Bibliography L

… ►

VOIGTL – A fast subroutine for Voigt function evaluation on vector processors. Comput. Phys. Comm. 75 (1-2), pp. 135–142.

ⓘ

Notes:

Single-precision Fortran, minimum accuracy 13D.

External Links:

Document, Code, ZentralBlatt

Referenced by:

3rd item.

Encodings:

BibTeX

…

9: Bibliography W

… ►

Rapid approximation to the Voigt/Faddeeva function and its derivatives. J. Quant. Spect. and Rad. Transfer 62 (1), pp. 29–48.

ⓘ

Notes:

Includes Fortran code in the appendices to compute the functions to an accuracy between ${10}^{-2}$ and ${10}^{-5}$.

External Links:

ISSN 0022-4073, Document

Referenced by:

§7.21, §7.21.

Encodings:

BibTeX

…

10: 7.25 Software

… ►

§7.25(ii) $\mathrm{erf}x$, $\mathrm{erfc}x$, ${\mathrm{i}}^n\mathrm{erfc}\left(x\right)$, $x\in ℝ$

… ►

§7.25(iii) $\mathrm{erf}z$, $\mathrm{erfc}z$, $w\left(z\right)$, $z\in ℂ$

… ►No research software has been found for these functions. … ►

§7.25(vi) $ℱ\left(x\right)$, $G\left(x\right)$, $𝖴(x,t)$, $𝖵(x,t)$, $x\in ℝ$

… ►No research software has been found for these functions. …