7 Error Functions, Dawson’s and Fresnel Integrals Properties 7.17 Inverse Error Functions 7.19 Voigt Functions

§7.18 Repeated Integrals of the Complementary Error Function

ⓘ

Keywords:: error functions, repeated integrals of, repeated integrals of the complementary error function
Referenced by:: §12.7(ii)
Permalink:: http://dlmf.nist.gov/7.18
See also:: Annotations for Ch.7

§7.18(i) Definition
§7.18(ii) Graphics
§7.18(iii) Properties
§7.18(iv) Relations to Other Functions
§7.18(v) Continued Fraction
§7.18(vi) Asymptotic Expansion

§7.18(i) Definition

ⓘ

Keywords:: definition, repeated integrals of the complementary error function
Permalink:: http://dlmf.nist.gov/7.18.i
See also:: Annotations for §7.18 and Ch.7

7.18.1	$\displaystyle\mathop{\mathrm{i}^{-1}\mathrm{erfc}}\left(z\right)$	$\displaystyle=\frac{2}{\sqrt{\pi}}e^{-z^{2}},$
7.18.1	$\displaystyle\mathop{\mathrm{i}^{0}\mathrm{erfc}}\left(z\right)$	$\displaystyle=\operatorname{erfc}z,$
ⓘ Symbols: $\pi$ : the ratio of the circumference of a circle to its diameter, $\operatorname{erfc}\NVar{z}$ : complementary error function, $\mathrm{e}$ : base of natural logarithm, $\mathop{\mathrm{i}^{\NVar{n}}\mathrm{erfc}}\left(\NVar{z}\right)$ : repeated integrals of the complementary error function and $z$ : complex variable A&S Ref: 7.2.1 (in modified form) Referenced by: §7.22(iii) Permalink: http://dlmf.nist.gov/7.18.E1 Encodings: TeX, TeX, pMML, pMML, png, png See also: Annotations for §7.18(i), §7.18 and Ch.7

and for $n=0,1,2,\dots$ ,

7.18.2		$\mathop{\mathrm{i}^{n}\mathrm{erfc}}\left(z\right)=\int_{z}^{\infty}\mathop{% \mathrm{i}^{n-1}\mathrm{erfc}}\left(t\right)\,\mathrm{d}t=\frac{2}{\sqrt{\pi}}% \int_{z}^{\infty}\frac{(t-z)^{n}}{n!}e^{-t^{2}}\,\mathrm{d}t.$
ⓘ Defines: $\mathop{\mathrm{i}^{\NVar{n}}\mathrm{erfc}}\left(\NVar{z}\right)$ : repeated integrals of the complementary error function Symbols: $\pi$ : the ratio of the circumference of a circle to its diameter, $\,\mathrm{d}\NVar{x}$ : differential of $x$ , $\mathrm{e}$ : base of natural logarithm, $!$ : factorial (as in $n!$ ), $\int$ : integral, $z$ : complex variable and $n$ : nonnegative integer A&S Ref: 7.2.1 (in modified form) 7.2.3 Permalink: http://dlmf.nist.gov/7.18.E2 Encodings: TeX, pMML, png See also: Annotations for §7.18(i), §7.18 and Ch.7

§7.18(ii) Graphics

ⓘ

Keywords:: repeated integrals of the complementary error function, scaled
Notes:: These graphs were produced at NIST.
Permalink:: http://dlmf.nist.gov/7.18.ii
See also:: Annotations for §7.18 and Ch.7

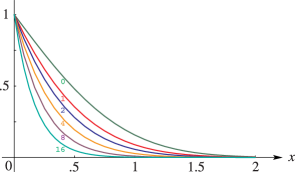
See accompanying text — Figure 7.18.1: Repeated integrals of the scaled complementary error function $2^{n}\Gamma\left(\tfrac{1}{2}n+1\right)\mathop{\mathrm{i}^{n}\mathrm{erfc}}% \left(x\right)$ , $n=0,1,2,4,8,16$ . Magnify

§7.18(iii) Properties

ⓘ

Keywords:: derivatives, differential equation, power-series expansion, recurrence relations, repeated integrals of the complementary error function
Notes:: See Hartree (1936).
Permalink:: http://dlmf.nist.gov/7.18.iii
See also:: Annotations for §7.18 and Ch.7

7.18.3		$\frac{\mathrm{d}}{\mathrm{d}z}\mathop{\mathrm{i}^{n}\mathrm{erfc}}\left(z% \right)=-\mathop{\mathrm{i}^{n-1}\mathrm{erfc}}\left(z\right),$
$n=0,1,2,\dots$ ,
ⓘ Symbols: $\frac{\mathrm{d}\NVar{f}}{\mathrm{d}\NVar{x}}$ : derivative of $f$ with respect to $x$ , $\mathop{\mathrm{i}^{\NVar{n}}\mathrm{erfc}}\left(\NVar{z}\right)$ : repeated integrals of the complementary error function, $z$ : complex variable and $n$ : nonnegative integer A&S Ref: 7.2.8 Permalink: http://dlmf.nist.gov/7.18.E3 Encodings: TeX, pMML, png See also: Annotations for §7.18(iii), §7.18 and Ch.7

7.18.4		$\frac{{\mathrm{d}}^{n}}{{\mathrm{d}z}^{n}}\left(e^{z^{2}}\operatorname{erfc}z% \right)=(-1)^{n}2^{n}n!e^{z^{2}}\mathop{\mathrm{i}^{n}\mathrm{erfc}}\left(z% \right),$
$n=0,1,2,\dots$ .
ⓘ Symbols: $\operatorname{erfc}\NVar{z}$ : complementary error function, $\frac{\mathrm{d}\NVar{f}}{\mathrm{d}\NVar{x}}$ : derivative of $f$ with respect to $x$ , $\mathrm{e}$ : base of natural logarithm, $!$ : factorial (as in $n!$ ), $\mathop{\mathrm{i}^{\NVar{n}}\mathrm{erfc}}\left(\NVar{z}\right)$ : repeated integrals of the complementary error function, $z$ : complex variable and $n$ : nonnegative integer A&S Ref: 7.2.9 Permalink: http://dlmf.nist.gov/7.18.E4 Encodings: TeX, pMML, png See also: Annotations for §7.18(iii), §7.18 and Ch.7

7.18.5		$\frac{{\mathrm{d}}^{2}W}{{\mathrm{d}z}^{2}}+2z\frac{\mathrm{d}W}{\mathrm{d}z}-% 2nW=0,$
$W(z)=A\mathop{\mathrm{i}^{n}\mathrm{erfc}}\left(z\right)+B\mathop{\mathrm{i}^{% n}\mathrm{erfc}}\left(-z\right)$ ,
ⓘ Symbols: $\frac{\mathrm{d}\NVar{f}}{\mathrm{d}\NVar{x}}$ : derivative of $f$ with respect to $x$ , $\mathop{\mathrm{i}^{\NVar{n}}\mathrm{erfc}}\left(\NVar{z}\right)$ : repeated integrals of the complementary error function, $z$ : complex variable and $n$ : nonnegative integer A&S Ref: 7.2.2 Permalink: http://dlmf.nist.gov/7.18.E5 Encodings: TeX, pMML, png See also: Annotations for §7.18(iii), §7.18 and Ch.7

where $n=1,2,3,\dots$ , and $A$ , $B$ are arbitrary constants.

7.18.6		$\mathop{\mathrm{i}^{n}\mathrm{erfc}}\left(z\right)=\sum_{k=0}^{\infty}\frac{(-% 1)^{k}z^{k}}{2^{n-k}k!\Gamma\left(1+\frac{1}{2}(n-k)\right)}.$
ⓘ Symbols: $\Gamma\left(\NVar{z}\right)$ : gamma function, $!$ : factorial (as in $n!$ ), $\mathop{\mathrm{i}^{\NVar{n}}\mathrm{erfc}}\left(\NVar{z}\right)$ : repeated integrals of the complementary error function, $z$ : complex variable and $n$ : nonnegative integer A&S Ref: 7.2.4 Permalink: http://dlmf.nist.gov/7.18.E6 Encodings: TeX, pMML, png See also: Annotations for §7.18(iii), §7.18 and Ch.7

7.18.7		$\mathop{\mathrm{i}^{n}\mathrm{erfc}}\left(z\right)=-\frac{z}{n}\mathop{\mathrm% {i}^{n-1}\mathrm{erfc}}\left(z\right)+\frac{1}{2n}\mathop{\mathrm{i}^{n-2}% \mathrm{erfc}}\left(z\right),$
$n=1,2,3,\dots$ .
ⓘ Symbols: $\mathop{\mathrm{i}^{\NVar{n}}\mathrm{erfc}}\left(\NVar{z}\right)$ : repeated integrals of the complementary error function, $z$ : complex variable and $n$ : nonnegative integer A&S Ref: 7.2.5 Referenced by: §7.22(iii) Permalink: http://dlmf.nist.gov/7.18.E7 Encodings: TeX, pMML, png See also: Annotations for §7.18(iii), §7.18 and Ch.7

§7.18(iv) Relations to Other Functions

ⓘ

Notes:: See Hartree (1936).
Referenced by:: Erratum (V1.0.21) for Paragraph Confluent Hypergeometric Functions (in §7.18(iv))
Permalink:: http://dlmf.nist.gov/7.18.iv
See also:: Annotations for §7.18 and Ch.7

For the notation see §§18.3, 13.2(i), and 12.2.

Hermite Polynomials

ⓘ

Keywords:: Hermite polynomials, relations to other functions, repeated integrals of the complementary error function
See also:: Annotations for §7.18(iv), §7.18 and Ch.7

7.18.8		$(-1)^{n}\mathop{\mathrm{i}^{n}\mathrm{erfc}}\left(z\right)+\mathop{\mathrm{i}^% {n}\mathrm{erfc}}\left(-z\right)=\frac{i^{-n}}{2^{n-1}n!}H_{n}\left(iz\right).$
ⓘ Symbols: $H_{\NVar{n}}\left(\NVar{x}\right)$ : Hermite polynomial, $!$ : factorial (as in $n!$ ), $\mathrm{i}$ : imaginary unit, $\mathop{\mathrm{i}^{\NVar{n}}\mathrm{erfc}}\left(\NVar{z}\right)$ : repeated integrals of the complementary error function, $z$ : complex variable and $n$ : nonnegative integer A&S Ref: 7.2.11 Permalink: http://dlmf.nist.gov/7.18.E8 Encodings: TeX, pMML, png See also: Annotations for §7.18(iv), §7.18(iv), §7.18 and Ch.7

Confluent Hypergeometric Functions

ⓘ

Keywords:: confluent hypergeometric functions, relations to other functions, repeated integrals of error functions, repeated integrals of the complementary error function
Referenced by:: Erratum (V1.0.21) for Paragraph Confluent Hypergeometric Functions (in §7.18(iv))
Clarification (effective with 1.0.21):: A note about the multivalued nature of (7.18.10) was inserted just below it.
See also:: Annotations for §7.18(iv), §7.18 and Ch.7

7.18.9		$\mathop{\mathrm{i}^{n}\mathrm{erfc}}\left(z\right)=e^{-z^{2}}\left(\frac{1}{2^% {n}\Gamma\left(\tfrac{1}{2}n+1\right)}M\left(\tfrac{1}{2}n+\tfrac{1}{2},\tfrac% {1}{2},z^{2}\right)-\frac{z}{2^{n-1}\Gamma\left(\tfrac{1}{2}n+\tfrac{1}{2}% \right)}M\left(\tfrac{1}{2}n+1,\tfrac{3}{2},z^{2}\right)\right),$
ⓘ Symbols: $\Gamma\left(\NVar{z}\right)$ : gamma function, $M\left(\NVar{a},\NVar{b},\NVar{z}\right)$ : $={{}_{1}F_{1}}\left(\NVar{a};\NVar{b};\NVar{z}\right)$ Kummer confluent hypergeometric function, $\mathrm{e}$ : base of natural logarithm, $\mathop{\mathrm{i}^{\NVar{n}}\mathrm{erfc}}\left(\NVar{z}\right)$ : repeated integrals of the complementary error function, $z$ : complex variable and $n$ : nonnegative integer A&S Ref: 7.2.12 Permalink: http://dlmf.nist.gov/7.18.E9 Encodings: TeX, pMML, png See also: Annotations for §7.18(iv), §7.18(iv), §7.18 and Ch.7

7.18.10		$\mathop{\mathrm{i}^{n}\mathrm{erfc}}\left(z\right)=\frac{e^{-z^{2}}}{2^{n}% \sqrt{\pi}}U\left(\tfrac{1}{2}n+\tfrac{1}{2},\tfrac{1}{2},z^{2}\right).$
ⓘ Symbols: $U\left(\NVar{a},\NVar{b},\NVar{z}\right)$ : Kummer confluent hypergeometric function, $\pi$ : the ratio of the circumference of a circle to its diameter, $\mathrm{e}$ : base of natural logarithm, $\mathop{\mathrm{i}^{\NVar{n}}\mathrm{erfc}}\left(\NVar{z}\right)$ : repeated integrals of the complementary error function, $z$ : complex variable and $n$ : nonnegative integer Referenced by: §7.18(iv), §7.18(iv), Erratum (V1.0.21) for Paragraph Confluent Hypergeometric Functions (in §7.18(iv)) Permalink: http://dlmf.nist.gov/7.18.E10 Encodings: TeX, pMML, png See also: Annotations for §7.18(iv), §7.18(iv), §7.18 and Ch.7

The confluent hypergeometric function on the right-hand side of (7.18.10) is multivalued and in the sectors $\tfrac{1}{2}\pi<\left|\operatorname{ph}z\right|<\pi$ one has to use the analytic continuation formula (13.2.12).

Parabolic Cylinder Functions

ⓘ

Keywords:: parabolic cylinder functions, relations to other functions, repeated integrals of the complementary error function
See also:: Annotations for §7.18(iv), §7.18 and Ch.7

7.18.11		$\mathop{\mathrm{i}^{n}\mathrm{erfc}}\left(z\right)=\frac{e^{-z^{2}/2}}{\sqrt{2% ^{n-1}\pi}}U\left(n+\tfrac{1}{2},z\sqrt{2}\right).$
ⓘ Symbols: $\pi$ : the ratio of the circumference of a circle to its diameter, $\mathrm{e}$ : base of natural logarithm, $U\left(\NVar{a},\NVar{z}\right)$ : parabolic cylinder function, $\mathop{\mathrm{i}^{\NVar{n}}\mathrm{erfc}}\left(\NVar{z}\right)$ : repeated integrals of the complementary error function, $z$ : complex variable and $n$ : nonnegative integer A&S Ref: 7.2.13 Referenced by: §12.7(ii) Permalink: http://dlmf.nist.gov/7.18.E11 Encodings: TeX, pMML, png See also: Annotations for §7.18(iv), §7.18(iv), §7.18 and Ch.7

Probability Functions

ⓘ

Keywords:: parabolic cylinder functions, probability functions, relations to other functions, repeated integrals of the complementary error function
See also:: Annotations for §7.18(iv), §7.18 and Ch.7

7.18.12		$\mathop{\mathrm{i}^{n}\mathrm{erfc}}\left(z\right)=\frac{1}{\sqrt{2^{n-1}\pi}}% \mathit{Hh}_{n}\left(\sqrt{2}z\right).$
ⓘ Defines: $\mathit{Hh}_{\NVar{n}}\left(\NVar{z}\right)$ : probability function Symbols: $\pi$ : the ratio of the circumference of a circle to its diameter, $\mathop{\mathrm{i}^{\NVar{n}}\mathrm{erfc}}\left(\NVar{z}\right)$ : repeated integrals of the complementary error function, $z$ : complex variable and $n$ : nonnegative integer A&S Ref: 7.2.10 Referenced by: §12.7(ii) Permalink: http://dlmf.nist.gov/7.18.E12 Encodings: TeX, pMML, png See also: Annotations for §7.18(iv), §7.18(iv), §7.18 and Ch.7

See Jeffreys and Jeffreys (1956, §§23.081–23.09).

§7.18(v) Continued Fraction

ⓘ

Keywords:: continued fractions, repeated integrals of the complementary error function
Notes:: See Hartree (1936) and Lorentzen and Waadeland (1992, p. 577).
Permalink:: http://dlmf.nist.gov/7.18.v
See also:: Annotations for §7.18 and Ch.7

7.18.13		$\frac{\mathop{\mathrm{i}^{n}\mathrm{erfc}}\left(z\right)}{\mathop{\mathrm{i}^{% n-1}\mathrm{erfc}}\left(z\right)}=\cfrac{1/2}{z+\cfrac{(n+1)/2}{z+\cfrac{(n+2)% /2}{z+}}}\cdots,$
$\Re z>0$ .
ⓘ Symbols: $\Re$ : real part, $\mathop{\mathrm{i}^{\NVar{n}}\mathrm{erfc}}\left(\NVar{z}\right)$ : repeated integrals of the complementary error function, $z$ : complex variable and $n$ : nonnegative integer Permalink: http://dlmf.nist.gov/7.18.E13 Encodings: TeX, pMML, png See also: Annotations for §7.18(v), §7.18 and Ch.7

§7.18(vi) Asymptotic Expansion

ⓘ

Keywords:: asymptotic expansions, repeated integrals of the complementary error function
Notes:: See Hartree (1936).
Permalink:: http://dlmf.nist.gov/7.18.vi
See also:: Annotations for §7.18 and Ch.7

7.18.14		$\mathop{\mathrm{i}^{n}\mathrm{erfc}}\left(z\right)\sim\frac{2}{\sqrt{\pi}}% \frac{e^{-z^{2}}}{(2z)^{n+1}}\sum_{m=0}^{\infty}\frac{(-1)^{m}(2m+n)!}{n!m!(2z% )^{2m}},$
$z\to\infty$ , $\|\operatorname{ph}z\|\leq\tfrac{3}{4}\pi-\delta(<\tfrac{3}{4}\pi)$ .
ⓘ Symbols: $\sim$ : Poincaré asymptotic expansion, $\pi$ : the ratio of the circumference of a circle to its diameter, $\mathrm{e}$ : base of natural logarithm, $!$ : factorial (as in $n!$ ), $\operatorname{ph}$ : phase, $\mathop{\mathrm{i}^{\NVar{n}}\mathrm{erfc}}\left(\NVar{z}\right)$ : repeated integrals of the complementary error function, $z$ : complex variable and $n$ : nonnegative integer A&S Ref: 7.2.14 Permalink: http://dlmf.nist.gov/7.18.E14 Encodings: TeX, pMML, png See also: Annotations for §7.18(vi), §7.18 and Ch.7

7.17 Inverse Error Functions 7.19 Voigt Functions

Site Privacy Accessibility Privacy Program Copyrights Vulnerability Disclosure No Fear Act Policy FOIA Environmental Policy Scientific Integrity Information Quality Standards Commerce.gov Science.gov USA.gov