14 Legendre and Related Functions Real Arguments 14.19 Toroidal (or Ring) Functions 14.21 Definitions and Basic Properties

§14.20 Conical (or Mehler) Functions

Referenced by:: §14.2(ii), §14.20(i)
Permalink:: http://dlmf.nist.gov/14.20

§14.20(i) Definitions and Wronskians
§14.20(ii) Graphics
§14.20(iii) Behavior as $x\to 1$
§14.20(iv) Integral Representation
§14.20(v) Trigonometric Expansion
§14.20(vi) Generalized Mehler–Fock Transformation
§14.20(vii) Asymptotic Approximations: Large $\tau$ , Fixed $\mu$
§14.20(viii) Asymptotic Approximations: Large $\tau$ , $0\leq\mu\leq A\tau$
§14.20(ix) Asymptotic Approximations: Large $\mu$ , $0\leq\tau\leq A\mu$
§14.20(x) Zeros and Integrals

§14.20(i) Definitions and Wronskians

Notes:: (14.20.3) follows from (14.9.10) and (14.20.2). (14.20.4) and (14.20.5) follow from (14.2.3) and (14.20.3). (14.20.6) follows from (14.3.10) and (14.9.12).
Keywords:: conical functions
Referenced by:: §14.32
Permalink:: http://dlmf.nist.gov/14.20.i

Throughout §14.20 we assume that $\nu=-\frac{1}{2}+i\tau$ , with $\mu\geq 0$ and $\tau\geq 0$ . (14.2.2) takes the form

14.20.1 $\left(1-x^{2}\right)\frac{{d}^{2}w}{{dx}^{2}}-2x\frac{dw}{dx}-\left(\tau^{2}+% \frac{1}{4}+\frac{\mu^{2}}{1-x^{2}}\right)w=0.$

Symbols:: $\frac{df}{dx}$ : derivative of with respect to , : real variable, $\tau$ : real variable and $\mu$ : general order
Referenced by:: §14.20(i), §14.20(i), §14.32
Permalink:: http://dlmf.nist.gov/14.20.E1
Encodings:: TeX, pMML, png

Solutions are known as conical or Mehler functions. For and $\tau>0$ , a numerically satisfactory pair of real conical functions is $\mathop{\mathsf{P}^{{-\mu}}_{{-\frac{1}{2}+i\tau}}\/}\nolimits\!\left(x\right)$ and $\mathop{\mathsf{P}^{{-\mu}}_{{-\frac{1}{2}+i\tau}}\/}\nolimits\!\left(-x\right)$ .

Another real-valued solution $\mathop{\widehat{\mathsf{Q}}^{{-\mu}}_{{-\frac{1}{2}+i\tau}}\/}\nolimits\!% \left(x\right)$ of (14.20.1) was introduced in Dunster (1991). This is defined by

14.20.2 $\mathop{\widehat{\mathsf{Q}}^{{-\mu}}_{{-\frac{1}{2}+i\tau}}\/}\nolimits\!% \left(x\right)=\realpart{\left(e^{{\mu\pi i}}\mathop{\mathsf{Q}^{{-\mu}}_{{-% \frac{1}{2}+i\tau}}\/}\nolimits\!\left(x\right)\right)}-\tfrac{1}{2}\pi\mathop% {\sin\/}\nolimits\!\left(\mu\pi\right)\mathop{\mathsf{P}^{{-\mu}}_{{-\frac{1}{% 2}+i\tau}}\/}\nolimits\!\left(x\right).$

Defines:: $\mathop{\widehat{\mathsf{Q}}^{{-\mu}}_{{-\frac{1}{2}+i\tau}}\/}\nolimits\!% \left(x\right)$ : conical function
Symbols:: $\mathop{\mathsf{P}^{{\mu}}_{{\nu}}\/}\nolimits\!\left(x\right)$ : Ferrers function of the first kind, $\mathop{\mathsf{Q}^{{\mu}}_{{\nu}}\/}\nolimits\!\left(x\right)$ : Ferrers function of the second kind, : base of exponential function, $\realpart{}$ : real part, $\mathop{\sin\/}\nolimits z$ : sine function, : real variable, $\tau$ : real variable and $\mu$ : general order
Referenced by:: §14.20(i), §14.23
Permalink:: http://dlmf.nist.gov/14.20.E2
Encodings:: TeX, pMML, png

Equivalently,

14.20.3 $\mathop{\widehat{\mathsf{Q}}^{{-\mu}}_{{-\frac{1}{2}+i\tau}}\/}\nolimits\!% \left(x\right)=\frac{\pi e^{{-\tau\pi}}\mathop{\sin\/}\nolimits\!\left(\mu\pi% \right)\mathop{\sinh\/}\nolimits\!\left(\tau\pi\right)}{2({\mathop{\cosh\/}% \nolimits^{{2}}}\!\left(\tau\pi\right)-{\mathop{\sin\/}\nolimits^{{2}}}\!\left% (\mu\pi\right))}\mathop{\mathsf{P}^{{-\mu}}_{{-\frac{1}{2}+i\tau}}\/}\nolimits% \!\left(x\right)+\frac{\pi(e^{{-\tau\pi}}{\mathop{\cos\/}\nolimits^{{2}}}\!% \left(\mu\pi\right)+\mathop{\sinh\/}\nolimits\!\left(\tau\pi\right))}{2({% \mathop{\cosh\/}\nolimits^{{2}}}\!\left(\tau\pi\right)-{\mathop{\sin\/}% \nolimits^{{2}}}\!\left(\mu\pi\right))}\mathop{\mathsf{P}^{{-\mu}}_{{-\frac{1}% {2}+i\tau}}\/}\nolimits\!\left(-x\right).$

Symbols:: $\mathop{\mathsf{P}^{{\mu}}_{{\nu}}\/}\nolimits\!\left(x\right)$ : Ferrers function of the first kind, $\mathop{\widehat{\mathsf{Q}}^{{-\mu}}_{{-\frac{1}{2}+i\tau}}\/}\nolimits\!% \left(x\right)$ : conical function, $\mathop{\cos\/}\nolimits z$ : cosine function, : base of exponential function, $\mathop{\cosh\/}\nolimits z$ : hyperbolic cosine function, $\mathop{\sinh\/}\nolimits z$ : hyperbolic sine function, $\mathop{\sin\/}\nolimits z$ : sine function, : real variable, $\tau$ : real variable and $\mu$ : general order
Referenced by:: §14.20(i), §14.20(iii), §14.20(ix)
Permalink:: http://dlmf.nist.gov/14.20.E3
Encodings:: TeX, pMML, png

$\mathop{\widehat{\mathsf{Q}}^{{-\mu}}_{{-\frac{1}{2}+i\tau}}\/}\nolimits\!% \left(x\right)$ exists except when $\mu=\frac{1}{2},\frac{3}{2},\dots$ and $\tau=0$ ; compare §14.3(i). It is an important companion solution to $\mathop{\mathsf{P}^{{-\mu}}_{{-\frac{1}{2}+i\tau}}\/}\nolimits\!\left(x\right)$ when $\tau$ is large; compare §§14.20(vii), 14.20(viii), and 10.25(iii).

14.20.4 $\mathop{\mathscr{W}\/}\nolimits\left\{\mathop{\mathsf{P}^{{-\mu}}_{{-\frac{1}{% 2}+i\tau}}\/}\nolimits\!\left(x\right),\mathop{\mathsf{P}^{{-\mu}}_{{-\frac{1}% {2}+i\tau}}\/}\nolimits\!\left(-x\right)\right\}=\frac{2}{|\mathop{\Gamma\/}% \nolimits\!\left(\mu+\frac{1}{2}+i\tau\right)|^{2}(1-x^{2})}.$

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, $\mathop{\mathsf{P}^{{\mu}}_{{\nu}}\/}\nolimits\!\left(x\right)$ : Ferrers function of the first kind, $\mathop{\mathscr{W}\/}\nolimits$ : Wronskian, : real variable, $\tau$ : real variable and $\mu$ : general order
Referenced by:: §14.20(i)
Permalink:: http://dlmf.nist.gov/14.20.E4
Encodings:: TeX, pMML, png

14.20.5 $\mathop{\mathscr{W}\/}\nolimits\left\{\mathop{\mathsf{P}^{{-\mu}}_{{-\frac{1}{% 2}+i\tau}}\/}\nolimits\!\left(x\right),\mathop{\widehat{\mathsf{Q}}^{{-\mu}}_{% {-\frac{1}{2}+i\tau}}\/}\nolimits\!\left(x\right)\right\}=\frac{\pi(e^{{-\tau% \pi}}{\mathop{\cos\/}\nolimits^{{2}}}\!\left(\mu\pi\right)+\mathop{\sinh\/}% \nolimits\!\left(\tau\pi\right))}{|\mathop{\Gamma\/}\nolimits\!\left(\mu+\frac% {1}{2}+i\tau\right)|^{2}({\mathop{\cosh\/}\nolimits^{{2}}}\!\left(\tau\pi% \right)-{\mathop{\sin\/}\nolimits^{{2}}}\!\left(\mu\pi\right))(1-x^{2})},$

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, $\mathop{\mathsf{P}^{{\mu}}_{{\nu}}\/}\nolimits\!\left(x\right)$ : Ferrers function of the first kind, $\mathop{\widehat{\mathsf{Q}}^{{-\mu}}_{{-\frac{1}{2}+i\tau}}\/}\nolimits\!% \left(x\right)$ : conical function, $\mathop{\mathscr{W}\/}\nolimits$ : Wronskian, $\mathop{\cos\/}\nolimits z$ : cosine function, : base of exponential function, $\mathop{\cosh\/}\nolimits z$ : hyperbolic cosine function, $\mathop{\sinh\/}\nolimits z$ : hyperbolic sine function, $\mathop{\sin\/}\nolimits z$ : sine function, : real variable, $\tau$ : real variable and $\mu$ : general order
Referenced by:: §14.20(i)
Permalink:: http://dlmf.nist.gov/14.20.E5
Encodings:: TeX, pMML, png

provided that $\mathop{\widehat{\mathsf{Q}}^{{-\mu}}_{{-\frac{1}{2}+i\tau}}\/}\nolimits\!% \left(x\right)$ exists.

Lastly, for the range $1<x<\infty$ , $\mathop{P^{{-\mu}}_{{-\frac{1}{2}+i\tau}}\/}\nolimits\!\left(x\right)$ is a real-valued solution of (14.20.1); in terms of $\mathop{Q^{{\mu}}_{{-\frac{1}{2}\pm i\tau}}\/}\nolimits\!\left(x\right)$ (which are complex-valued in general):

14.20.6 $\mathop{P^{{-\mu}}_{{-\frac{1}{2}+i\tau}}\/}\nolimits\!\left(x\right)=\frac{ie% ^{{-\mu\pi i}}}{\mathop{\sinh\/}\nolimits\!\left(\tau\pi\right)\left|\mathop{% \Gamma\/}\nolimits\!\left(\mu+\frac{1}{2}+i\tau\right)\right|^{2}}\*\left(% \mathop{Q^{{\mu}}_{{-\frac{1}{2}+i\tau}}\/}\nolimits\!\left(x\right)-\mathop{Q% ^{{\mu}}_{{-\frac{1}{2}-i\tau}}\/}\nolimits\!\left(x\right)\right),$ $\tau\neq 0$ .

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, $\mathop{P^{{\mu}}_{{\nu}}\/}\nolimits\!\left(z\right)$ : associated Legendre function of the first kind, $\mathop{Q^{{\mu}}_{{\nu}}\/}\nolimits\!\left(z\right)$ : associated Legendre function of the second kind, : base of exponential function, $\mathop{\sinh\/}\nolimits z$ : hyperbolic sine function, : real variable, $\tau$ : real variable and $\mu$ : general order
Referenced by:: §14.20(i)
Permalink:: http://dlmf.nist.gov/14.20.E6
Encodings:: TeX, pMML, png

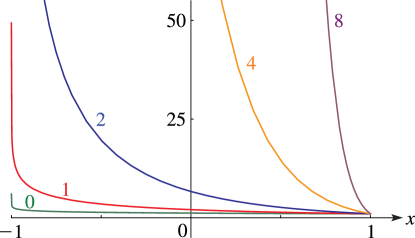
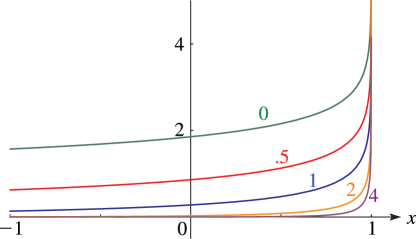
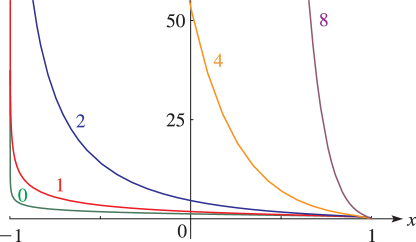
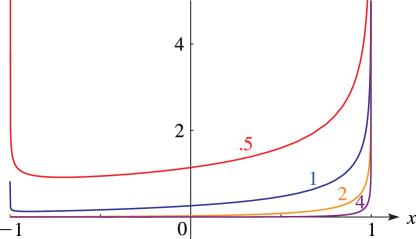
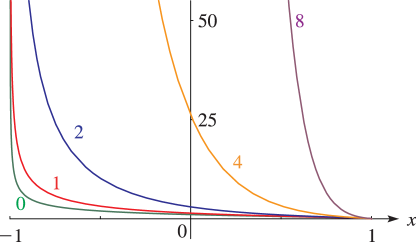
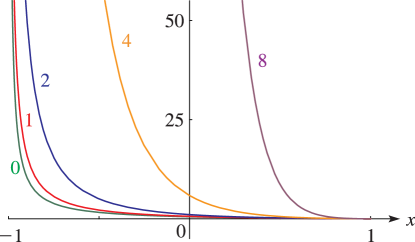
§14.20(ii) Graphics

Notes:: These graphs were produced at NIST.
Keywords:: conical functions
Permalink:: http://dlmf.nist.gov/14.20.ii

Figure 14.20.1: $\mathop{\mathsf{P}^{{0}}_{{-\frac{1}{2}+i\tau}}\/}\nolimits\!\left(x\right),% \tau=0,1,2,4,8$ .

Symbols:: $\mathop{\mathsf{P}^{{\mu}}_{{\nu}}\/}\nolimits\!\left(x\right)$ : Ferrers function of the first kind, : real variable and $\tau$ : real variable
Permalink:: http://dlmf.nist.gov/14.20.F1
Encodings:: pdf, png

Figure 14.20.2: $\mathop{\widehat{\mathsf{Q}}^{{0}}_{{-\frac{1}{2}+i\tau}}\/}\nolimits\!\left(x% \right),\tau=0,\tfrac{1}{2},1,2,4$ .

Symbols:: $\mathop{\widehat{\mathsf{Q}}^{{-\mu}}_{{-\frac{1}{2}+i\tau}}\/}\nolimits\!% \left(x\right)$ : conical function, : real variable and $\tau$ : real variable
Permalink:: http://dlmf.nist.gov/14.20.F2
Encodings:: pdf, png

Figure 14.20.3: $\mathop{\mathsf{P}^{{-1/2}}_{{-\frac{1}{2}+i\tau}}\/}\nolimits\!\left(x\right)% ,\tau=0,1,2,4,8$ .

Symbols:: $\mathop{\mathsf{P}^{{\mu}}_{{\nu}}\/}\nolimits\!\left(x\right)$ : Ferrers function of the first kind, : real variable and $\tau$ : real variable
Permalink:: http://dlmf.nist.gov/14.20.F3
Encodings:: pdf, png

Figure 14.20.4: $\mathop{\widehat{\mathsf{Q}}^{{-1/2}}_{{-\frac{1}{2}+i\tau}}\/}\nolimits\!% \left(x\right)$ , $\tau=\tfrac{1}{2},1,2,4$ . (This function does not exist when $\tau=0$ .)

Symbols:: $\mathop{\widehat{\mathsf{Q}}^{{-\mu}}_{{-\frac{1}{2}+i\tau}}\/}\nolimits\!% \left(x\right)$ : conical function, : real variable and $\tau$ : real variable
Permalink:: http://dlmf.nist.gov/14.20.F4
Encodings:: pdf, png

Figure 14.20.5: $\mathop{\mathsf{P}^{{-1}}_{{-\frac{1}{2}+i\tau}}\/}\nolimits\!\left(x\right),% \tau=0,1,2,4,8$ .

Symbols:: $\mathop{\mathsf{P}^{{\mu}}_{{\nu}}\/}\nolimits\!\left(x\right)$ : Ferrers function of the first kind, : real variable and $\tau$ : real variable
Permalink:: http://dlmf.nist.gov/14.20.F5
Encodings:: pdf, png

Figure 14.20.6: $\mathop{\widehat{\mathsf{Q}}^{{-1}}_{{-\frac{1}{2}+i\tau}}\/}\nolimits\!\left(% x\right),\tau=0,\tfrac{1}{2},1,2,4$ .

Symbols:: $\mathop{\widehat{\mathsf{Q}}^{{-\mu}}_{{-\frac{1}{2}+i\tau}}\/}\nolimits\!% \left(x\right)$ : conical function, : real variable and $\tau$ : real variable
Permalink:: http://dlmf.nist.gov/14.20.F6
Encodings:: pdf, png

Figure 14.20.7: $\mathop{\mathsf{P}^{{-2}}_{{-\frac{1}{2}+i\tau}}\/}\nolimits\!\left(x\right),% \tau=0,1,2,4,8$ .

Symbols:: $\mathop{\mathsf{P}^{{\mu}}_{{\nu}}\/}\nolimits\!\left(x\right)$ : Ferrers function of the first kind, : real variable and $\tau$ : real variable
Permalink:: http://dlmf.nist.gov/14.20.F7
Encodings:: pdf, png

Figure 14.20.8: $\mathop{\widehat{\mathsf{Q}}^{{-2}}_{{-\frac{1}{2}+i\tau}}\/}\nolimits\!\left(% x\right),\tau=0,\tfrac{1}{2},1,2,4$ .

Symbols:: $\mathop{\widehat{\mathsf{Q}}^{{-\mu}}_{{-\frac{1}{2}+i\tau}}\/}\nolimits\!% \left(x\right)$ : conical function, : real variable and $\tau$ : real variable
Permalink:: http://dlmf.nist.gov/14.20.F8
Encodings:: pdf, png

§14.20(iii) Behavior as $x\to 1$

Notes:: (14.20.7) and (14.20.8) may be derived from §14.8(i) and (14.20.3).
Keywords:: conical functions
Permalink:: http://dlmf.nist.gov/14.20.iii

The behavior of $\mathop{\mathsf{P}^{{-\mu}}_{{-\frac{1}{2}+i\tau}}\/}\nolimits\!\left(\pm x\right)$ as $x\to 1-$ is given in §14.8(i). For $\mu>0$ and $x\to 1-$ ,

14.20.7 $\mathop{\widehat{\mathsf{Q}}^{{\mu}}_{{-\frac{1}{2}+i\tau}}\/}\nolimits\!\left% (x\right)\sim\tfrac{1}{2}\mathop{\Gamma\/}\nolimits\!\left(\mu\right)\left(% \frac{2}{1-x}\right)^{{\mu/2}},$

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, $\mathop{\widehat{\mathsf{Q}}^{{-\mu}}_{{-\frac{1}{2}+i\tau}}\/}\nolimits\!% \left(x\right)$ : conical function, $\sim$ : asymptotic equality, : real variable, $\tau$ : real variable and $\mu$ : general order
Referenced by:: §14.20(iii)
Permalink:: http://dlmf.nist.gov/14.20.E7
Encodings:: TeX, pMML, png

14.20.8 $\mathop{\widehat{\mathsf{Q}}^{{-\mu}}_{{-\frac{1}{2}+i\tau}}\/}\nolimits\!% \left(x\right)\sim\frac{\pi\mathop{\Gamma\/}\nolimits\!\left(\mu\right)(e^{{-% \tau\pi}}{\mathop{\cos\/}\nolimits^{{2}}}\!\left(\mu\pi\right)+\mathop{\sinh\/% }\nolimits\!\left(\tau\pi\right))}{2({\mathop{\cosh\/}\nolimits^{{2}}}\!\left(% \tau\pi\right)-{\mathop{\sin\/}\nolimits^{{2}}}\!\left(\mu\pi\right))\left|% \mathop{\Gamma\/}\nolimits\!\left(\mu+\frac{1}{2}+i\tau\right)\right|^{2}}\*% \left(\frac{2}{1-x}\right)^{{\mu/2}}.$

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, $\mathop{\widehat{\mathsf{Q}}^{{-\mu}}_{{-\frac{1}{2}+i\tau}}\/}\nolimits\!% \left(x\right)$ : conical function, $\mathop{\cos\/}\nolimits z$ : cosine function, : base of exponential function, $\mathop{\cosh\/}\nolimits z$ : hyperbolic cosine function, $\mathop{\sinh\/}\nolimits z$ : hyperbolic sine function, $\sim$ : asymptotic equality, $\mathop{\sin\/}\nolimits z$ : sine function, : real variable, $\tau$ : real variable and $\mu$ : general order
Referenced by:: §14.20(iii)
Permalink:: http://dlmf.nist.gov/14.20.E8
Encodings:: TeX, pMML, png

§14.20(iv) Integral Representation

Notes:: (14.20.9) may be derived from (14.12.1).
Keywords:: conical functions
Referenced by:: §14.32
Permalink:: http://dlmf.nist.gov/14.20.iv

When $0<\theta<\pi$ ,

14.20.9 $\mathop{\mathsf{P}_{{-\frac{1}{2}+i\tau}}\/}\nolimits\!\left(\mathop{\cos\/}% \nolimits\theta\right)=\frac{2}{\pi}\int_{{0}}^{{\theta}}\frac{\mathop{\cosh\/% }\nolimits\!\left(\tau\phi\right)}{\sqrt{2(\mathop{\cos\/}\nolimits\phi-% \mathop{\cos\/}\nolimits\theta)}}d\phi.$

Symbols:: $\mathop{\mathsf{P}^{{\mu}}_{{\nu}}\/}\nolimits\!\left(x\right)$ : Ferrers function of the first kind, $\mathop{\cos\/}\nolimits z$ : cosine function, : differential of , $\mathop{\cosh\/}\nolimits z$ : hyperbolic cosine function, $\int$ : integral, $\tau$ : real variable and $0<\theta<\pi$ : variable
A&S Ref:: 8.12.3
Referenced by:: §14.20(iv), §14.20(v)
Permalink:: http://dlmf.nist.gov/14.20.E9
Encodings:: TeX, pMML, png

§14.20(v) Trigonometric Expansion

Notes:: See Erdélyi et al. (1953a, p. 174).
Keywords:: conical functions
Permalink:: http://dlmf.nist.gov/14.20.v

14.20.10 $\mathop{\mathsf{P}_{{-\frac{1}{2}+i\tau}}\/}\nolimits\!\left(\mathop{\cos\/}% \nolimits\theta\right)=1+\frac{4\tau^{2}+1^{2}}{2^{2}}{\mathop{\sin\/}% \nolimits^{{2}}}\!\left(\tfrac{1}{2}\theta\right)+\frac{\left(4\tau^{2}+1^{2}% \right)\left(4\tau^{2}+3^{2}\right)}{2^{2}\cdot 4^{2}}{\mathop{\sin\/}% \nolimits^{{4}}}\!\left(\tfrac{1}{2}\theta\right)+\cdots,$ $0\leq\theta\leq\pi$ .

Symbols:: $\mathop{\mathsf{P}^{{\mu}}_{{\nu}}\/}\nolimits\!\left(x\right)$ : Ferrers function of the first kind, $\mathop{\cos\/}\nolimits z$ : cosine function, $\mathop{\sin\/}\nolimits z$ : sine function and $\tau$ : real variable
A&S Ref:: 8.12.1
Referenced by:: §14.20(v)
Permalink:: http://dlmf.nist.gov/14.20.E10
Encodings:: TeX, pMML, png

From (14.20.9) or (14.20.10) it is evident that $\mathop{\mathsf{P}_{{-\frac{1}{2}+i\tau}}\/}\nolimits\!\left(\mathop{\cos\/}% \nolimits\theta\right)$ is positive for real $\theta$ .

§14.20(vi) Generalized Mehler–Fock Transformation

Notes:: See Braaksma and Meulenbeld (1967).
Keywords:: Mehler–Fock transformation, conical functions
Referenced by:: §14.31(ii)
Permalink:: http://dlmf.nist.gov/14.20.vi

14.20.11 $f(\tau)=\frac{\tau}{\pi}\mathop{\sinh\/}\nolimits\!\left(\tau\pi\right)\mathop% {\Gamma\/}\nolimits\!\left(\tfrac{1}{2}-\mu+i\tau\right)\*\mathop{\Gamma\/}% \nolimits\!\left(\tfrac{1}{2}-\mu-i\tau\right)\int_{{1}}^{{\infty}}\mathop{P^{% {\mu}}_{{-\frac{1}{2}+i\tau}}\/}\nolimits\!\left(x\right)g(x)dx,$

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, $\mathop{P^{{\mu}}_{{\nu}}\/}\nolimits\!\left(z\right)$ : associated Legendre function of the first kind, : differential of , $\mathop{\sinh\/}\nolimits z$ : hyperbolic sine function, $\int$ : integral, : real variable, $\tau$ : real variable and $\mu$ : general order
Permalink:: http://dlmf.nist.gov/14.20.E11
Encodings:: TeX, pMML, png

where

14.20.12 $g(x)=\int_{{0}}^{{\infty}}\mathop{P^{{\mu}}_{{-\frac{1}{2}+i\tau}}\/}\nolimits% \!\left(x\right)f(\tau)d\tau.$

Symbols:: $\mathop{P^{{\mu}}_{{\nu}}\/}\nolimits\!\left(z\right)$ : associated Legendre function of the first kind, : differential of , $\int$ : integral, : real variable, $\tau$ : real variable and $\mu$ : general order
Permalink:: http://dlmf.nist.gov/14.20.E12
Encodings:: TeX, pMML, png

Special cases:

14.20.13 $\mathop{P_{{-\frac{1}{2}+i\tau}}\/}\nolimits\!\left(x\right)=\frac{\mathop{% \cosh\/}\nolimits\!\left(\tau\pi\right)}{\pi}\int_{{1}}^{{\infty}}\frac{% \mathop{P_{{-\frac{1}{2}+i\tau}}\/}\nolimits\!\left(t\right)}{x+t}dt,$

Symbols:: $\mathop{P^{{\mu}}_{{\nu}}\/}\nolimits\!\left(z\right)$ : associated Legendre function of the first kind, : differential of , $\mathop{\cosh\/}\nolimits z$ : hyperbolic cosine function, $\int$ : integral, : real variable and $\tau$ : real variable
Permalink:: http://dlmf.nist.gov/14.20.E13
Encodings:: TeX, pMML, png

14.20.14 $\pi\int_{{0}}^{{\infty}}\frac{\tau\mathop{\tanh\/}\nolimits\!\left(\tau\pi% \right)}{\mathop{\cosh\/}\nolimits\!\left(\tau\pi\right)}\mathop{P_{{-\frac{1}% {2}+i\tau}}\/}\nolimits\!\left(x\right)\mathop{P_{{-\frac{1}{2}+i\tau}}\/}% \nolimits\!\left(y\right)d\tau=\frac{1}{y+x}.$

Symbols:: $\mathop{P^{{\mu}}_{{\nu}}\/}\nolimits\!\left(z\right)$ : associated Legendre function of the first kind, : differential of , $\mathop{\cosh\/}\nolimits z$ : hyperbolic cosine function, $\mathop{\tanh\/}\nolimits z$ : hyperbolic tangent function, $\int$ : integral, : real variable and $\tau$ : real variable
Permalink:: http://dlmf.nist.gov/14.20.E14
Encodings:: TeX, pMML, png

§14.20(vii) Asymptotic Approximations: Large $\tau$ , Fixed $\mu$

Notes:: For (14.20.15) see Olver (1997b, p. 473). (14.20.16) may be derived from (14.20.18).
Keywords:: conical functions
Referenced by:: §14.20(i), §14.32, §2.8(iv)
Permalink:: http://dlmf.nist.gov/14.20.vii

For $\tau\to\infty$ and fixed $\mu$ ,

14.20.15 $\mathop{\mathsf{P}^{{-\mu}}_{{-\frac{1}{2}+i\tau}}\/}\nolimits\!\left(\mathop{% \cos\/}\nolimits\theta\right)=\frac{1}{\tau^{{\mu}}}\left(\frac{\theta}{% \mathop{\sin\/}\nolimits\theta}\right)^{{1/2}}\mathop{I_{{\mu}}\/}\nolimits\!% \left(\tau\theta\right)\*\left(1+\mathop{O\/}\nolimits\!\left(\ifrac{1}{\tau}% \right)\right),$

Symbols:: $\mathop{O\/}\nolimits\!\left(x\right)$ : order not exceeding, $\mathop{\mathsf{P}^{{\mu}}_{{\nu}}\/}\nolimits\!\left(x\right)$ : Ferrers function of the first kind, $\mathop{\cos\/}\nolimits z$ : cosine function, $\mathop{I_{{\nu}}\/}\nolimits\!\left(z\right)$ : modified Bessel function, $\mathop{\sin\/}\nolimits z$ : sine function, $\tau$ : real variable, $\mu$ : general order and $0<\theta<\pi$ : variable
Referenced by:: §14.20(vii)
Permalink:: http://dlmf.nist.gov/14.20.E15
Encodings:: TeX, pMML, png

14.20.16 $\mathop{\widehat{\mathsf{Q}}^{{-\mu}}_{{-\frac{1}{2}+i\tau}}\/}\nolimits\!% \left(\mathop{\cos\/}\nolimits\theta\right)=\frac{1}{\tau^{{\mu}}}\left(\frac{% \theta}{\mathop{\sin\/}\nolimits\theta}\right)^{{1/2}}\mathop{K_{{\mu}}\/}% \nolimits\!\left(\tau\theta\right)\*\left(1+\mathop{O\/}\nolimits\!\left(% \ifrac{1}{\tau}\right)\right),$

Symbols:: $\mathop{O\/}\nolimits\!\left(x\right)$ : order not exceeding, $\mathop{\widehat{\mathsf{Q}}^{{-\mu}}_{{-\frac{1}{2}+i\tau}}\/}\nolimits\!% \left(x\right)$ : conical function, $\mathop{\cos\/}\nolimits z$ : cosine function, $\mathop{K_{{\nu}}\/}\nolimits\!\left(z\right)$ : modified Bessel function, $\mathop{\sin\/}\nolimits z$ : sine function, $\tau$ : real variable, $\mu$ : general order and $0<\theta<\pi$ : variable
Referenced by:: §14.20(vii)
Permalink:: http://dlmf.nist.gov/14.20.E16
Encodings:: TeX, pMML, png

uniformly for $\theta\in(0,\pi-\delta]$ , where $\mathop{I\/}\nolimits$ and $\mathop{K\/}\nolimits$ are the modified Bessel functions (§10.25(ii)) and $\delta$ is an arbitrary constant such that $0<\delta<\pi$ . For asymptotic expansions and explicit error bounds, see Olver (1997b, pp. 473–474). See also Žurina and Karmazina (1966).

§14.20(viii) Asymptotic Approximations: Large $\tau$ , $0\leq\mu\leq A\tau$

Notes:: See Dunster (1991).
Keywords:: conical functions
Referenced by:: §14.20(i), §2.8(vi)
Permalink:: http://dlmf.nist.gov/14.20.viii

In this subsection and §14.20(ix), and $\delta$ denote arbitrary constants such that and $0<\delta<2$ .

As $\tau\to\infty$ ,

14.20.17 $\mathop{\mathsf{P}^{{-\mu}}_{{-\frac{1}{2}+i\tau}}\/}\nolimits\!\left(x\right)% =\sigma(\mu,\tau)\left(\frac{\alpha^{2}+\eta}{1+\alpha^{2}-x^{2}}\right)^{{1/4% }}\mathop{I_{{\mu}}\/}\nolimits\!\left(\tau\eta^{{1/2}}\right)\*\left(1+% \mathop{O\/}\nolimits\!\left(\ifrac{1}{\tau}\right)\right),$

Symbols:: $\mathop{O\/}\nolimits\!\left(x\right)$ : order not exceeding, $\mathop{\mathsf{P}^{{\mu}}_{{\nu}}\/}\nolimits\!\left(x\right)$ : Ferrers function of the first kind, $\mathop{I_{{\nu}}\/}\nolimits\!\left(z\right)$ : modified Bessel function, : real variable, $\tau$ : real variable, $\mu$ : general order, $\alpha$ , $\sigma(\mu,\tau)$ and $\eta$
Permalink:: http://dlmf.nist.gov/14.20.E17
Encodings:: TeX, pMML, png

14.20.18 $\mathop{\widehat{\mathsf{Q}}^{{-\mu}}_{{-\frac{1}{2}+i\tau}}\/}\nolimits\!% \left(x\right)=\sigma(\mu,\tau)\left(\frac{\alpha^{2}+\eta}{1+\alpha^{2}-x^{2}% }\right)^{{1/4}}\mathop{K_{{\mu}}\/}\nolimits\!\left(\tau\eta^{{1/2}}\right)\*% \left(1+\mathop{O\/}\nolimits\!\left(\ifrac{1}{\tau}\right)\right),$

Symbols:: $\mathop{O\/}\nolimits\!\left(x\right)$ : order not exceeding, $\mathop{\widehat{\mathsf{Q}}^{{-\mu}}_{{-\frac{1}{2}+i\tau}}\/}\nolimits\!% \left(x\right)$ : conical function, $\mathop{K_{{\nu}}\/}\nolimits\!\left(z\right)$ : modified Bessel function, : real variable, $\tau$ : real variable, $\mu$ : general order, $\alpha$ , $\sigma(\mu,\tau)$ and $\eta$
Referenced by:: §14.20(vii)
Permalink:: http://dlmf.nist.gov/14.20.E18
Encodings:: TeX, pMML, png

uniformly for $x\in[-1+\delta,1)$ and $\mu\in[0,A\tau]$ . Here

14.20.19 $\alpha=\mu/\tau,$

Symbols:: $\tau$ : real variable, $\mu$ : general order and $\alpha$
Permalink:: http://dlmf.nist.gov/14.20.E19
Encodings:: TeX, pMML, png

14.20.20 $\sigma(\mu,\tau)=\frac{\mathop{\exp\/}\nolimits\!\left(\mu-\tau\mathop{\mathrm% {arctan}\/}\nolimits\alpha\right)}{\left(\mu^{2}+\tau^{2}\right)^{{\mu/2}}}.$

Symbols:: $\mathop{\exp\/}\nolimits z$ : exponential function, $\mathop{\mathrm{arctan}\/}\nolimits z$ : arctangent function, $\tau$ : real variable, $\mu$ : general order, $\alpha$ and $\sigma(\mu,\tau)$
Permalink:: http://dlmf.nist.gov/14.20.E20
Encodings:: TeX, pMML, png

The variable $\eta$ is defined implicitly by

14.20.21 ${\left(\alpha^{2}+\eta\right)^{{1/2}}+\tfrac{1}{2}\alpha\mathop{\ln\/}% \nolimits\eta-\alpha\mathop{\ln\/}\nolimits\!\left(\left(\alpha^{2}+\eta\right% )^{{1/2}}+\alpha\right)}={\mathop{\mathrm{arccos}\/}\nolimits\!\left(\frac{x}{% \left(1+\alpha^{2}\right)^{{1/2}}}\right)+\frac{\alpha}{2}\mathop{\ln\/}% \nolimits\!\left(\frac{1+\alpha^{2}+\left(\alpha^{2}-1\right)x^{2}-2\alpha x% \left(1+\alpha^{2}-x^{2}\right)^{{1/2}}}{\left(1+\alpha^{2}\right)\left(1-x^{2% }\right)}\right)},$

Symbols:: $\mathop{\mathrm{arccos}\/}\nolimits z$ : arccosine function, $\mathop{\ln\/}\nolimits z$ : principal branch of logarithm function, : real variable, $\alpha$ and $\eta$
Permalink:: http://dlmf.nist.gov/14.20.E21
Encodings:: TeX, pMML, png

where the inverse trigonometric functions take their principal values. The interval is mapped one-to-one to the interval $0<\eta<\infty$ , with the points and corresponding to $\eta=\infty$ and $\eta=0$ , respectively.

For extensions to complex arguments (including the range $1<x<\infty$ ), asymptotic expansions, and explicit error bounds, see Dunster (1991).

§14.20(ix) Asymptotic Approximations: Large $\mu$ , $0\leq\tau\leq A\mu$

Notes:: See Dunster (1991, Eqs. (5.11) and (5.14) have been corrected).
Keywords:: conical functions
Referenced by:: §14.20(viii), §14.32
Permalink:: http://dlmf.nist.gov/14.20.ix

As $\mu\to\infty$ ,

14.20.22 $\mathop{\mathsf{P}^{{-\mu}}_{{-\frac{1}{2}+i\tau}}\/}\nolimits\!\left(x\right)% =\frac{\beta\mathop{\exp\/}\nolimits\!\left(\mu\beta\mathop{\mathrm{arctan}\/}% \nolimits\beta\right)}{\mathop{\Gamma\/}\nolimits\!\left(\mu+1\right)\left(1+% \beta^{2}\right)^{{\mu/2}}}\frac{e^{{-\mu\rho}}}{\left(1+\beta^{2}-x^{2}\beta^% {2}\right)^{{1/4}}}\left(1+\mathop{O\/}\nolimits\!\left(\frac{1}{\mu}\right)% \right),$

Symbols:: $\mathop{O\/}\nolimits\!\left(x\right)$ : order not exceeding, $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, $\mathop{\mathsf{P}^{{\mu}}_{{\nu}}\/}\nolimits\!\left(x\right)$ : Ferrers function of the first kind, $\mathop{\exp\/}\nolimits z$ : exponential function, : base of exponential function, $\mathop{\mathrm{arctan}\/}\nolimits z$ : arctangent function, : real variable, $\tau$ : real variable, $\mu$ : general order, $\beta$ and $\rho$
Referenced by:: §14.20(ix)
Permalink:: http://dlmf.nist.gov/14.20.E22
Encodings:: TeX, pMML, png

uniformly for $x\in(-1,1)$ and $\tau\in[0,A\mu]$ . Here

14.20.23 $\beta=\tau/\mu,$

Symbols:: $\tau$ : real variable, $\mu$ : general order and $\beta$
Permalink:: http://dlmf.nist.gov/14.20.E23
Encodings:: TeX, pMML, png

and the variable $\rho$ is defined by

14.20.24 $\rho=\frac{1}{2}\mathop{\ln\/}\nolimits\!\left(\frac{\left(1-\beta^{2}\right)x% ^{2}+1+\beta^{2}+2x\left(1+\beta^{2}-\beta^{2}x^{2}\right)^{{1/2}}}{1-x^{2}}% \right)+\beta\mathop{\mathrm{arctan}\/}\nolimits\!\left(\frac{\beta x}{\sqrt{1% +\beta^{2}-\beta^{2}x^{2}}}\right)-\frac{1}{2}\mathop{\ln\/}\nolimits\!\left(1% +\beta^{2}\right),$

Symbols:: $\mathop{\mathrm{arctan}\/}\nolimits z$ : arctangent function, $\mathop{\ln\/}\nolimits z$ : principal branch of logarithm function, : real variable, $\beta$ and $\rho$
Permalink:: http://dlmf.nist.gov/14.20.E24
Encodings:: TeX, pMML, png

with the inverse tangent taking its principal value. The interval is mapped one-to-one to the interval $-\infty<\rho<\infty$ , with the points , , and corresponding to $\rho=-\infty$ , $\rho=0$ , and $\rho=\infty$ , respectively.

With the same conditions, the corresponding approximation for $\mathop{\mathsf{P}^{{-\mu}}_{{-\frac{1}{2}+i\tau}}\/}\nolimits\!\left(-x\right)$ is obtainable by replacing $e^{{-\mu\rho}}$ by $e^{{\mu\rho}}$ on the right-hand side of (14.20.22). Approximations for $\mathop{\mathsf{P}^{{\mu}}_{{-\frac{1}{2}+i\tau}}\/}\nolimits\!\left(x\right)$ and $\mathop{\widehat{\mathsf{Q}}^{{-\mu}}_{{-\frac{1}{2}+i\tau}}\/}\nolimits\!% \left(x\right)$ can then be achieved via (14.9.7) and (14.20.3).

For extensions to complex arguments (including the range $1<x<\infty$ ), asymptotic expansions, and explicit error bounds, see Dunster (1991).

§14.20(x) Zeros and Integrals

Keywords:: conical functions
Permalink:: http://dlmf.nist.gov/14.20.x

For zeros of $\mathop{\mathsf{P}_{{-\frac{1}{2}+i\tau}}\/}\nolimits\!\left(x\right)$ see Hobson (1931, §237).

For integrals with respect to $\tau$ involving $\mathop{\mathsf{P}_{{-\frac{1}{2}+i\tau}}\/}\nolimits\!\left(x\right)$ , see Prudnikov et al. (1990, pp. 218–228).

© 2010–2013 NIST / Privacy Policy / Disclaimer / Feedback; Version 1.0.6; Release date 2013-05-06 Math-Image version (See MathML) . A Printed Companionis available. 14.19 Toroidal (or Ring) Functions 14.21 Definitions and Basic Properties

§14.20 Conical (or Mehler) Functions

Contents