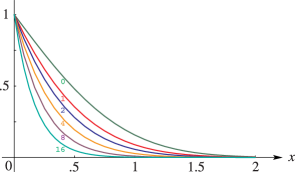
scaled gamma function

SearchAdvancedHelp

(0.008 seconds)

11—20 of 40 matching pages

11: 7.18 Repeated Integrals of the Complementary Error Function

… ►

►►

Figure 7.18.1: Repeated integrals of the scaled complementary error function $2^n\mathrm{\Gamma }\left(\frac{1}{2}n+1\right){\mathrm{i}}^n\mathrm{erfc}\left(x\right)$, $n=0,1,2,4,8,16$. Magnify

…

12: 14.1 Special Notation

… ► ►►►

$x$, $y$, $\tau$	real variables.
…
$𝐅(a,b;c;z)$	Olver’s scaled hypergeometric function: $F(a,b;c;z)/\mathrm{\Gamma }\left(c\right)$.

…

13: 30.15 Signal Analysis

… ►

§30.15(i) Scaled Spheroidal Wave Functions

… ► ►

§30.15(iv) Orthogonality

… ►

§30.15(v) Extremal Properties

… ►

14: 10.22 Integrals

… ►

10.22.49 $${\int }_0^{\mathrm{\infty }}{t}^{\mu -1}{\mathrm{e}}^{-at}{J}_{\nu }\left(bt\right)dt=\frac{{(\frac{1}{2}b)}^{\nu }}{a^{\mu +\nu }}\mathrm{\Gamma }\left(\mu +\nu \right)𝐅(\frac{\mu +\nu }{2},\frac{\mu +\nu +1}{2};\nu +1;-\frac{b^2}{a^2}),$$ $\mathrm{\Re }\left(\mu +\nu \right)>0,\mathrm{\Re }\left(a\pm \mathrm{i}b\right)>0$,

ⓘ

Symbols:

$J_{\nu }\left(z\right)$: Bessel function of the first kind, $\mathrm{\Gamma }\left(z\right)$: gamma function, $dx$: differential of $x$ , $\mathrm{e}$: base of natural logarithm, $\mathrm{i}$: imaginary unit, $\int$: integral, $\mathrm{\Re }$: real part, $𝐅(a,b;c;z)$ or $𝐅(\genfrac{}{}{0pt}{}{a,b}{c};z)$: $={}_2{}^{}𝐅_1^{}(a,b;c;z)$ Olver’s hypergeometric function and $\nu$: complex parameter

Keywords:

Laplace transform, Mellin transform

Referenced by:

§10.22(iv)

Permalink:

http://dlmf.nist.gov/10.22.E49

Encodings:

pMML, png, TeX

See also:

Annotations for §10.22(iv), §10.22 and Ch.10

►

10.22.50 $${\int }_0^{\mathrm{\infty }}{t}^{\mu -1}{\mathrm{e}}^{-at}{Y}_{\nu }\left(bt\right)dt=\cot \left(\nu \pi \right)\frac{{(\frac{1}{2}b)}^{\nu }\mathrm{\Gamma }\left(\mu +\nu \right)}{{(a^2+b^2)}^{\frac{1}{2}(\mu +\nu )}}𝐅(\frac{\mu +\nu }{2},\frac{1-\mu +\nu }{2};\nu +1;\frac{b^2}{a^2+b^2})-\csc \left(\nu \pi \right)\frac{{(\frac{1}{2}b)}^{-\nu }\mathrm{\Gamma }\left(\mu -\nu \right)}{{(a^2+b^2)}^{\frac{1}{2}(\mu -\nu )}}𝐅(\frac{\mu -\nu }{2},\frac{1-\mu -\nu }{2};1-\nu ;\frac{b^2}{a^2+b^2}),$$ $\mathrm{\Re }\mu >|\mathrm{\Re }\nu |,\mathrm{\Re }\left(a\pm \mathrm{i}b\right)>0$.

ⓘ

Symbols:

$Y_{\nu }\left(z\right)$: Bessel function of the second kind, $\mathrm{\Gamma }\left(z\right)$: gamma function, $\pi$: the ratio of the circumference of a circle to its diameter, $\csc z$: cosecant function, $\cot z$: cotangent function, $dx$: differential of $x$ , $\mathrm{e}$: base of natural logarithm, $\mathrm{i}$: imaginary unit, $\int$: integral, $\mathrm{\Re }$: real part, $𝐅(a,b;c;z)$ or $𝐅(\genfrac{}{}{0pt}{}{a,b}{c};z)$: $={}_2{}^{}𝐅_1^{}(a,b;c;z)$ Olver’s hypergeometric function and $\nu$: complex parameter

Permalink:

http://dlmf.nist.gov/10.22.E50

Encodings:

pMML, png, TeX

See also:

Annotations for §10.22(iv), §10.22 and Ch.10

… ►

10.22.56 $${\int }_0^{\mathrm{\infty }}\frac{J_{\mu }\left(at\right)J_{\nu }\left(bt\right)}{t^{\lambda }}dt=\frac{a^{\mu }\mathrm{\Gamma }\left(\frac{1}{2}\nu +\frac{1}{2}\mu -\frac{1}{2}\lambda +\frac{1}{2}\right)}{2^{\lambda }{b}^{\mu -\lambda +1}\mathrm{\Gamma }\left(\frac{1}{2}\nu -\frac{1}{2}\mu +\frac{1}{2}\lambda +\frac{1}{2}\right)}𝐅(\frac{1}{2}(\mu +\nu -\lambda +1),\frac{1}{2}(\mu -\nu -\lambda +1);\mu +1;\frac{a^2}{b^2}),$$ , $\mathrm{\Re }\left(\mu +\nu +1\right)>\mathrm{\Re }\lambda >-1$.

ⓘ

Symbols:

$J_{\nu }\left(z\right)$: Bessel function of the first kind, $\mathrm{\Gamma }\left(z\right)$: gamma function, $dx$: differential of $x$ , $\int$: integral, $\mathrm{\Re }$: real part, $𝐅(a,b;c;z)$ or $𝐅(\genfrac{}{}{0pt}{}{a,b}{c};z)$: $={}_2{}^{}𝐅_1^{}(a,b;c;z)$ Olver’s hypergeometric function and $\nu$: complex parameter

Keywords:

Mellin transform

A&S Ref:

11.4.33, 11.4.34

Referenced by:

§10.22(iv)

Permalink:

http://dlmf.nist.gov/10.22.E56

Encodings:

pMML, png, TeX

See also:

Annotations for §10.22(iv), §10.22(iv), §10.22 and Ch.10

… ►

10.22.58 $${\int }_0^{\mathrm{\infty }}\frac{J_{\nu }\left(at\right)J_{\nu }\left(bt\right)}{t^{\lambda }}dt=\frac{{(ab)}^{\nu }\mathrm{\Gamma }\left(\nu -\frac{1}{2}\lambda +\frac{1}{2}\right)}{2^{\lambda }{(a^2+b^2)}^{\nu -\frac{1}{2}\lambda +\frac{1}{2}}\mathrm{\Gamma }\left(\frac{1}{2}\lambda +\frac{1}{2}\right)}𝐅(\frac{2\nu +1-\lambda }{4},\frac{2\nu +3-\lambda }{4};\nu +1;\frac{4a^2{b}^2}{{(a^2+b^2)}^2}),$$ $a\ne b$, $\mathrm{\Re }\left(2\nu +1\right)>\mathrm{\Re }\lambda >-1$.

ⓘ

Symbols:

$J_{\nu }\left(z\right)$: Bessel function of the first kind, $\mathrm{\Gamma }\left(z\right)$: gamma function, $dx$: differential of $x$ , $\int$: integral, $\mathrm{\Re }$: real part, $𝐅(a,b;c;z)$ or $𝐅(\genfrac{}{}{0pt}{}{a,b}{c};z)$: $={}_2{}^{}𝐅_1^{}(a,b;c;z)$ Olver’s hypergeometric function and $\nu$: complex parameter

Keywords:

Mellin transform

Permalink:

http://dlmf.nist.gov/10.22.E58

Encodings:

pMML, png, TeX

See also:

Annotations for §10.22(iv), §10.22(iv), §10.22 and Ch.10

… ►

10.22.64

ⓘ

Symbols:

$J_{\nu }\left(z\right)$: Bessel function of the first kind, $\mathrm{\Gamma }\left(z\right)$: gamma function, $dx$: differential of $x$ , $!$: factorial (as in $n!$), $\int$: integral, $𝐅(a,b;c;z)$ or $𝐅(\genfrac{}{}{0pt}{}{a,b}{c};z)$: $={}_2{}^{}𝐅_1^{}(a,b;c;z)$ Olver’s hypergeometric function and $n$: integer

Referenced by:

§10.22(iv), §10.59

Permalink:

http://dlmf.nist.gov/10.22.E64

Encodings:

pMML, png, TeX

See also:

Annotations for §10.22(iv), §10.22(iv), §10.22 and Ch.10

…

15: 15.8 Transformations of Variable

… ►

15.8.2 $$\frac{\sin \left(\pi (b-a)\right)}{\pi }𝐅(\genfrac{}{}{0pt}{}{a,b}{c};z)=\frac{{(-z)}^{-a}}{\mathrm{\Gamma }\left(b\right)\mathrm{\Gamma }\left(c-a\right)}𝐅(\genfrac{}{}{0pt}{}{a,a-c+1}{a-b+1};\frac{1}{z})-\frac{{(-z)}^{-b}}{\mathrm{\Gamma }\left(a\right)\mathrm{\Gamma }\left(c-b\right)}𝐅(\genfrac{}{}{0pt}{}{b,b-c+1}{b-a+1};\frac{1}{z}),$$ .

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{ph}$: phase, $𝐅(a,b;c;z)$ or $𝐅(\genfrac{}{}{0pt}{}{a,b}{c};z)$: $={}_2{}^{}𝐅_1^{}(a,b;c;z)$ Olver’s hypergeometric function, $\sin z$: sine function, $z$: complex variable, $a$: real or complex parameter, $b$: real or complex parameter and $c$: real or complex parameter

Referenced by:

§15.12(i), §15.16, §15.8(i), §15.8(i), §15.8(ii), §15.8(ii), §15.8(ii)

Permalink:

http://dlmf.nist.gov/15.8.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §15.8(i), §15.8 and Ch.15

►

15.8.3 $$\frac{\sin \left(\pi (b-a)\right)}{\pi }𝐅(\genfrac{}{}{0pt}{}{a,b}{c};z)=\frac{{(1-z)}^{-a}}{\mathrm{\Gamma }\left(b\right)\mathrm{\Gamma }\left(c-a\right)}𝐅(\genfrac{}{}{0pt}{}{a,c-b}{a-b+1};\frac{1}{1-z})-\frac{{(1-z)}^{-b}}{\mathrm{\Gamma }\left(a\right)\mathrm{\Gamma }\left(c-b\right)}𝐅(\genfrac{}{}{0pt}{}{b,c-a}{b-a+1};\frac{1}{1-z}),$$ .

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{ph}$: phase, $𝐅(a,b;c;z)$ or $𝐅(\genfrac{}{}{0pt}{}{a,b}{c};z)$: $={}_2{}^{}𝐅_1^{}(a,b;c;z)$ Olver’s hypergeometric function, $\sin z$: sine function, $z$: complex variable, $a$: real or complex parameter, $b$: real or complex parameter and $c$: real or complex parameter

Referenced by:

§15.8(i), §15.8(ii)

Permalink:

http://dlmf.nist.gov/15.8.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §15.8(i), §15.8 and Ch.15

►

15.8.4 $$\frac{\sin \left(\pi (c-a-b)\right)}{\pi }𝐅(\genfrac{}{}{0pt}{}{a,b}{c};z)=\frac{1}{\mathrm{\Gamma }\left(c-a\right)\mathrm{\Gamma }\left(c-b\right)}𝐅(\genfrac{}{}{0pt}{}{a,b}{a+b-c+1};1-z)-\frac{{(1-z)}^{c-a-b}}{\mathrm{\Gamma }\left(a\right)\mathrm{\Gamma }\left(b\right)}𝐅(\genfrac{}{}{0pt}{}{c-a,c-b}{c-a-b+1};1-z),$$ , .

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{ph}$: phase, $𝐅(a,b;c;z)$ or $𝐅(\genfrac{}{}{0pt}{}{a,b}{c};z)$: $={}_2{}^{}𝐅_1^{}(a,b;c;z)$ Olver’s hypergeometric function, $\sin z$: sine function, $z$: complex variable, $a$: real or complex parameter, $b$: real or complex parameter and $c$: real or complex parameter

Referenced by:

§15.16, §15.19(iv), §15.2(i), §15.4(ii), §15.8(i), §15.8(i), §15.8(ii)

Permalink:

http://dlmf.nist.gov/15.8.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §15.8(i), §15.8 and Ch.15

►

15.8.5 $$\frac{\sin \left(\pi (c-a-b)\right)}{\pi }𝐅(\genfrac{}{}{0pt}{}{a,b}{c};z)=\frac{z^{-a}}{\mathrm{\Gamma }\left(c-a\right)\mathrm{\Gamma }\left(c-b\right)}𝐅(\genfrac{}{}{0pt}{}{a,a-c+1}{a+b-c+1};1-\frac{1}{z})-\frac{{(1-z)}^{c-a-b}{z}^{a-c}}{\mathrm{\Gamma }\left(a\right)\mathrm{\Gamma }\left(b\right)}𝐅(\genfrac{}{}{0pt}{}{c-a,1-a}{c-a-b+1};1-\frac{1}{z}),$$ , .

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{ph}$: phase, $𝐅(a,b;c;z)$ or $𝐅(\genfrac{}{}{0pt}{}{a,b}{c};z)$: $={}_2{}^{}𝐅_1^{}(a,b;c;z)$ Olver’s hypergeometric function, $\sin z$: sine function, $z$: complex variable, $a$: real or complex parameter, $b$: real or complex parameter and $c$: real or complex parameter

Referenced by:

§15.8(i), §15.8(i), §15.8(ii), §15.8(ii), §15.8(ii)

Permalink:

http://dlmf.nist.gov/15.8.E5

Encodings:

pMML, png, TeX

See also:

Annotations for §15.8(i), §15.8 and Ch.15

… ►

15.8.10 $$𝐅(\genfrac{}{}{0pt}{}{a,b}{a+b+m};z)=\frac{1}{\mathrm{\Gamma }\left(a+m\right)\mathrm{\Gamma }\left(b+m\right)}\sum _{k=0}^{m-1}\frac{{\left(a\right)}_k{\left(b\right)}_k(m-k-1)!}{k!}{(z-1)}^k-\frac{{(z-1)}^m}{\mathrm{\Gamma }\left(a\right)\mathrm{\Gamma }\left(b\right)}\sum _{k=0}^{\mathrm{\infty }}\frac{{\left(a+m\right)}_k{\left(b+m\right)}_k}{k!(k+m)!}{(1-z)}^k\left(\ln \left(1-z\right)-\psi \left(k+1\right)-\psi \left(k+m+1\right)+\psi \left(a+k+m\right)+\psi \left(b+k+m\right)\right),$$ ,

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, ${\left(a\right)}_n$: Pochhammer’s symbol (or shifted factorial), $\pi$: the ratio of the circumference of a circle to its diameter, $\psi \left(z\right)$: psi (or digamma) function, $!$: factorial (as in $n!$), $\ln z$: principal branch of logarithm function, $\mathrm{ph}$: phase, $𝐅(a,b;c;z)$ or $𝐅(\genfrac{}{}{0pt}{}{a,b}{c};z)$: $={}_2{}^{}𝐅_1^{}(a,b;c;z)$ Olver’s hypergeometric function, $z$: complex variable, $a$: real or complex parameter, $b$: real or complex parameter, $k$: integer and $m$: integer

Referenced by:

§15.4(ii), §15.8(ii)

Permalink:

http://dlmf.nist.gov/15.8.E10

Encodings:

pMML, png, TeX

Correction (effective with 1.1.2):

Pochhammer symbols now link to their definition.

See also:

Annotations for §15.8(ii), §15.8 and Ch.15

…

16: 15.2 Definitions and Analytical Properties

… ►

15.2.2 $$𝐅(a,b;c;z)=\sum _{s=0}^{\mathrm{\infty }}\frac{{\left(a\right)}_s{\left(b\right)}_s}{\mathrm{\Gamma }\left(c+s\right)s!}{z}^s,$$ ,

ⓘ

Defines:

$𝐅(a,b;c;z)$ or $𝐅(\genfrac{}{}{0pt}{}{a,b}{c};z)$: $={}_2{}^{}𝐅_1^{}(a,b;c;z)$ Olver’s hypergeometric function

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, ${\left(a\right)}_n$: Pochhammer’s symbol (or shifted factorial), $!$: factorial (as in $n!$), ${}_p{}^{}𝐅_q^{}(𝐚;𝐛;z)$ or ${}_p{}^{}𝐅_q^{}(\genfrac{}{}{0pt}{}{𝐚}{𝐛};z)$: scaled (or Olver’s) generalized hypergeometric function, $s$: nonnegative integer, $z$: complex variable, $a$: real or complex parameter, $b$: real or complex parameter and $c$: real or complex parameter

Referenced by:

§15.12(i), §16.2(v)

Permalink:

http://dlmf.nist.gov/15.2.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §15.2(i), §15.2 and Ch.15

… ►

15.2.3 $$𝐅(\genfrac{}{}{0pt}{}{a,b}{c};x+\mathrm{i}0)-𝐅(\genfrac{}{}{0pt}{}{a,b}{c};x-\mathrm{i}0)=\frac{2\pi \mathrm{i}}{\mathrm{\Gamma }\left(a\right)\mathrm{\Gamma }\left(b\right)}{(x-1)}^{c-a-b}𝐅(\genfrac{}{}{0pt}{}{c-a,c-b}{c-a-b+1};1-x),$$ $x>1$.

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{i}$: imaginary unit, $𝐅(a,b;c;z)$ or $𝐅(\genfrac{}{}{0pt}{}{a,b}{c};z)$: $={}_2{}^{}𝐅_1^{}(a,b;c;z)$ Olver’s hypergeometric function, $x$: real variable, $a$: real or complex parameter, $b$: real or complex parameter and $c$: real or complex parameter

Referenced by:

§15.2(i)

Permalink:

http://dlmf.nist.gov/15.2.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §15.2(i), §15.2 and Ch.15

… ►

15.2.3_5 $$\underset{c\to -n}{lim}\frac{F(a,b;c;z)}{\mathrm{\Gamma }\left(c\right)}=𝐅(a,b;-n;z)=\frac{{\left(a\right)}_{n+1}{\left(b\right)}_{n+1}}{(n+1)!}{z}^{n+1}F(a+n+1,b+n+1;n+2;z),$$ $n=0,1,2,\mathrm{\dots }$.

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $F(a,b;c;z)$ or $F(\genfrac{}{}{0pt}{}{a,b}{c};z)$: $={}_2{}^{}F_1^{}(a,b;c;z)$ Gauss’ hypergeometric function, ${\left(a\right)}_n$: Pochhammer’s symbol (or shifted factorial), $!$: factorial (as in $n!$), $𝐅(a,b;c;z)$ or $𝐅(\genfrac{}{}{0pt}{}{a,b}{c};z)$: $={}_2{}^{}𝐅_1^{}(a,b;c;z)$ Olver’s hypergeometric function, $n$: integer, $z$: complex variable, $a$: real or complex parameter, $b$: real or complex parameter and $c$: real or complex parameter

Referenced by:

§15.2(ii), Erratum (V1.0.28) for Equations (15.2.3_5), (19.11.6_5)

Permalink:

http://dlmf.nist.gov/15.2.E3_5

Encodings:

pMML, png, TeX

Clarification (effective with 1.0.28):

This equation was given a number.

See also:

Annotations for §15.2(ii), §15.2 and Ch.15

…

17: 15.6 Integral Representations

… ►

15.6.1 $$𝐅(a,b;c;z)=\frac{1}{\mathrm{\Gamma }\left(b\right)\mathrm{\Gamma }\left(c-b\right)}{\int }_0^1\frac{t^{b-1}{(1-t)}^{c-b-1}}{{(1-zt)}^a}dt,$$ ; $\mathrm{\Re }c>\mathrm{\Re }b>0$.

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $\pi$: the ratio of the circumference of a circle to its diameter, $dx$: differential of $x$ , $\int$: integral, $\mathrm{ph}$: phase, $\mathrm{\Re }$: real part, $𝐅(a,b;c;z)$ or $𝐅(\genfrac{}{}{0pt}{}{a,b}{c};z)$: $={}_2{}^{}𝐅_1^{}(a,b;c;z)$ Olver’s hypergeometric function, $z$: complex variable, $a$: real or complex parameter, $b$: real or complex parameter and $c$: real or complex parameter

Keywords:

Mellin transform

Referenced by:

§15.19(iii), (15.4.34), §15.6, §15.6, Erratum (V1.0.23) for Equations (15.6.1)–(15.6.9), Erratum (V1.0.23) for Equations (15.6.1)–(15.6.9)

Permalink:

http://dlmf.nist.gov/15.6.E1

Encodings:

pMML, png, TeX

Addition (effective with 1.0.23):

The Olver hypergeometric function $𝐅(a,b;c;z)$, previously omitted from the left-hand side to make the formula more concise, has been added. The constraint , originally mentioned in the text, has been directly added to the formula.

See also:

Annotations for §15.6 and Ch.15

►

15.6.2 $$𝐅(a,b;c;z)=\frac{\mathrm{\Gamma }\left(1+b-c\right)}{2\pi \mathrm{i}\mathrm{\Gamma }\left(b\right)}{\int }_0^{(1+)}\frac{t^{b-1}{(t-1)}^{c-b-1}}{{(1-zt)}^a}dt,$$ ; $c-b\ne 1,2,3,\mathrm{\dots }$, $\mathrm{\Re }b>0$.

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $\pi$: the ratio of the circumference of a circle to its diameter, $dx$: differential of $x$ , $\mathrm{i}$: imaginary unit, $\int$: integral, $\mathrm{ph}$: phase, $\mathrm{\Re }$: real part, $𝐅(a,b;c;z)$ or $𝐅(\genfrac{}{}{0pt}{}{a,b}{c};z)$: $={}_2{}^{}𝐅_1^{}(a,b;c;z)$ Olver’s hypergeometric function, $z$: complex variable, $a$: real or complex parameter, $b$: real or complex parameter and $c$: real or complex parameter

Keywords:

Mellin transform

Referenced by:

§15.6

Permalink:

http://dlmf.nist.gov/15.6.E2

Encodings:

pMML, png, TeX

Addition (effective with 1.0.23):

The Olver hypergeometric function $𝐅(a,b;c;z)$, previously omitted from the left-hand side to make the formula more concise, has been added. The constraint , originally mentioned in the text, has been directly added to the formula.

See also:

Annotations for §15.6 and Ch.15

►

15.6.2_5 $$𝐅(a,b;c;z)=\frac{1}{\mathrm{\Gamma }\left(b\right)\mathrm{\Gamma }\left(c-b\right)}{\int }_0^{\mathrm{\infty }}\frac{t^{b-1}{\left(t+1\right)}^{a-c}}{{\left(t-zt+1\right)}^a}dt,$$ ; $\mathrm{\Re }c>\mathrm{\Re }b>0$.

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $\pi$: the ratio of the circumference of a circle to its diameter, $dx$: differential of $x$ , $\int$: integral, $\mathrm{ph}$: phase, $\mathrm{\Re }$: real part, $𝐅(a,b;c;z)$ or $𝐅(\genfrac{}{}{0pt}{}{a,b}{c};z)$: $={}_2{}^{}𝐅_1^{}(a,b;c;z)$ Olver’s hypergeometric function, $z$: complex variable, $a$: real or complex parameter, $b$: real or complex parameter and $c$: real or complex parameter

Keywords:

Mellin transform

Referenced by:

§15.6, Erratum (V1.1.5) for Additions

Permalink:

http://dlmf.nist.gov/15.6.E2_5

Encodings:

pMML, png, TeX

Addition (effective with 1.1.5):

This equation was added.

See also:

Annotations for §15.6 and Ch.15

… ►

15.6.6 $$𝐅(a,b;c;z)=\frac{1}{2\pi \mathrm{i}\mathrm{\Gamma }\left(a\right)\mathrm{\Gamma }\left(b\right)}{\int }_{-\mathrm{i}\mathrm{\infty }}^{\mathrm{i}\mathrm{\infty }}\frac{\mathrm{\Gamma }\left(a+t\right)\mathrm{\Gamma }\left(b+t\right)\mathrm{\Gamma }\left(-t\right)}{\mathrm{\Gamma }\left(c+t\right)}{(-z)}^{t}dt,$$ ; $a,b\ne 0,-1,-2,\mathrm{\dots }$.

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $\pi$: the ratio of the circumference of a circle to its diameter, $dx$: differential of $x$ , $\mathrm{i}$: imaginary unit, $\int$: integral, $\mathrm{ph}$: phase, $𝐅(a,b;c;z)$ or $𝐅(\genfrac{}{}{0pt}{}{a,b}{c};z)$: $={}_2{}^{}𝐅_1^{}(a,b;c;z)$ Olver’s hypergeometric function, $z$: complex variable, $a$: real or complex parameter, $b$: real or complex parameter and $c$: real or complex parameter

A&S Ref:

15.3.2 (modified)

Referenced by:

§15.6, §15.6, Erratum (V1.0.23) for Equations (15.6.1)–(15.6.9)

Permalink:

http://dlmf.nist.gov/15.6.E6

Encodings:

pMML, png, TeX

Addition (effective with 1.0.23):

The Olver hypergeometric function $𝐅(a,b;c;z)$, previously omitted from the left-hand side to make the formula more concise, has been added. The constraint , originally mentioned in the text, has been directly added to the formula.

See also:

Annotations for §15.6 and Ch.15

… ►

15.6.8 $$𝐅(a,b;c;z)=\frac{1}{\mathrm{\Gamma }\left(c-d\right)}{\int }_0^1𝐅(a,b;d;zt)t^{d-1}{(1-t)}^{c-d-1}dt,$$ ; $\mathrm{\Re }c>\mathrm{\Re }d>0$.

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $\pi$: the ratio of the circumference of a circle to its diameter, $dx$: differential of $x$ , $\int$: integral, $\mathrm{ph}$: phase, $\mathrm{\Re }$: real part, $𝐅(a,b;c;z)$ or $𝐅(\genfrac{}{}{0pt}{}{a,b}{c};z)$: $={}_2{}^{}𝐅_1^{}(a,b;c;z)$ Olver’s hypergeometric function, $z$: complex variable, $a$: real or complex parameter, $b$: real or complex parameter and $c$: real or complex parameter

Keywords:

Mellin transform

Proof sketch:

Follows from (15.6.9) with $\lambda =a+b$.

Referenced by:

(15.6.9), §15.6, §15.6, §15.6, §18.17(iv), Erratum (V1.0.14) for Equation (15.6.8), Erratum (V1.0.14) for Equation (15.6.8)

Permalink:

http://dlmf.nist.gov/15.6.E8

Encodings:

pMML, png, TeX

Addition (effective with 1.0.23):

The Olver hypergeometric function $𝐅(a,b;c;z)$, previously omitted from the left-hand side to make the formula more concise, has been added. The constraint , originally mentioned in the text, has been directly added to the formula.

See also:

Annotations for §15.6 and Ch.15

…

18: 10.43 Integrals

… ►

10.43.26 $${\int }_0^{\mathrm{\infty }}\frac{K_{\mu }\left(at\right)J_{\nu }\left(bt\right)}{t^{\lambda }}dt=\frac{b^{\nu }\mathrm{\Gamma }\left(\frac{1}{2}\nu -\frac{1}{2}\lambda +\frac{1}{2}\mu +\frac{1}{2}\right)\mathrm{\Gamma }\left(\frac{1}{2}\nu -\frac{1}{2}\lambda -\frac{1}{2}\mu +\frac{1}{2}\right)}{2^{\lambda +1}{a}^{\nu -\lambda +1}}𝐅(\frac{\nu -\lambda +\mu +1}{2},\frac{\nu -\lambda -\mu +1}{2};\nu +1;-\frac{b^2}{a^2}),$$ $\mathrm{\Re }\left(\nu +1-\lambda \right)>|\mathrm{\Re }\mu |,\mathrm{\Re }a>|\mathrm{\Im }b|$.

ⓘ

Symbols:

$J_{\nu }\left(z\right)$: Bessel function of the first kind, $\mathrm{\Gamma }\left(z\right)$: gamma function, $dx$: differential of $x$ , $\mathrm{\Im }$: imaginary part, $\int$: integral, $K_{\nu }\left(z\right)$: modified Bessel function of the second kind, $\mathrm{\Re }$: real part, $𝐅(a,b;c;z)$ or $𝐅(\genfrac{}{}{0pt}{}{a,b}{c};z)$: $={}_2{}^{}𝐅_1^{}(a,b;c;z)$ Olver’s hypergeometric function and $\nu$: complex parameter

Keywords:

Mellin transform

Permalink:

http://dlmf.nist.gov/10.43.E26

Encodings:

pMML, png, TeX

See also:

Annotations for §10.43(iv), §10.43 and Ch.10

…

19: 14.19 Toroidal (or Ring) Functions

… ►

14.19.2 $$P_{\nu -\frac{1}{2}}^{\mu }\left(\cosh \xi \right)=\frac{\mathrm{\Gamma }\left(\frac{1}{2}-\mu \right)}{{\pi }^{1/2}{\left(1-{\mathrm{e}}^{-2\xi }\right)}^{\mu }{\mathrm{e}}^{(\nu +(1/2))\xi }}𝐅(\frac{1}{2}-\mu ,\frac{1}{2}+\nu -\mu ;1-2\mu ;1-{\mathrm{e}}^{-2\xi }),$$ $\mu \ne \frac{1}{2},\frac{3}{2},\frac{5}{2},\mathrm{\dots }$.

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $P_{\nu }^{\mu }\left(z\right)$: associated Legendre function of the first kind, $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{e}$: base of natural logarithm, $\cosh z$: hyperbolic cosine function, $𝐅(a,b;c;z)$ or $𝐅(\genfrac{}{}{0pt}{}{a,b}{c};z)$: $={}_2{}^{}𝐅_1^{}(a,b;c;z)$ Olver’s hypergeometric function, $\mu$: general order, $\nu$: general degree and $\xi >0$: variable

Referenced by:

§14.19(ii), Erratum (V1.0.1) for Equation (14.19.2)

Permalink:

http://dlmf.nist.gov/14.19.E2

Encodings:

pMML, png, TeX

Errata (effective with 1.0.1):

Originally the argument to $𝐅$ was incorrect and the condition on $\mu$ too weak:

$$P_{\nu -\frac{1}{2}}^{\mu }\left(\cosh \xi \right)=\frac{\mathrm{\Gamma }\left(1-2\mu \right)2^{2\mu }}{\mathrm{\Gamma }\left(1-\mu \right){\left(1-{\mathrm{e}}^{-2\xi }\right)}^{\mu }{\mathrm{e}}^{(\nu +(1/2))\xi }}𝐅(\frac{1}{2}-\mu ,\frac{1}{2}+\nu -\mu ;1-2\mu ;{\mathrm{e}}^{-2\xi }),$$ $\mu \ne \frac{1}{2}$.

Also, the factor multiplying $𝐅$ was rewritten to clarify the poles, which determine the correct condition on $\mu$.

Reported 2010-11-02 by Alvaro Valenzuela

See also:

Annotations for §14.19(ii), §14.19 and Ch.14

…

20: 15.9 Relations to Other Functions

… ►

15.9.16 $$𝐅(\genfrac{}{}{0pt}{}{a,b}{2b};z)=\frac{\sqrt{\pi }}{\mathrm{\Gamma }\left(b\right)}{z}^{-b+(1/2)}{(1-z)}^{(b-a-(1/2))/2}{P}_{a-b-(1/2)}^{-b+(1/2)}\left(\frac{2-z}{2\sqrt{1-z}}\right),$$ $b\ne 0,-1,-2,\mathrm{\dots }$, and .

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $P_{\nu }^{\mu }\left(z\right)$: associated Legendre function of the first kind, $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{ph}$: phase, $𝐅(a,b;c;z)$ or $𝐅(\genfrac{}{}{0pt}{}{a,b}{c};z)$: $={}_2{}^{}𝐅_1^{}(a,b;c;z)$ Olver’s hypergeometric function, $z$: complex variable, $a$: real or complex parameter and $b$: real or complex parameter

Permalink:

http://dlmf.nist.gov/15.9.E16

Encodings:

pMML, png, TeX

See also:

Annotations for §15.9(iv), §15.9 and Ch.15

… ►

15.9.22 $$𝐅(\genfrac{}{}{0pt}{}{a,b}{\frac{1}{2}};z)=\frac{2^{a+b-(3/2)}}{\pi }\mathrm{\Gamma }\left(a+\frac{1}{2}\right)\mathrm{\Gamma }\left(b+\frac{1}{2}\right){(z-1)}^{(-a-b+(1/2))/2}\left({\mathrm{e}}^{\pm \pi \mathrm{i}(a+b-(1/2))}{P}_{a-b-(1/2)}^{-a-b+(1/2)}\left(-\sqrt{z}\right)+P_{a-b-(1/2)}^{-a-b+(1/2)}\left(\sqrt{z}\right)\right),$$ $a,b\ne -\frac{1}{2},-\frac{3}{2},-\frac{5}{2},\mathrm{\dots }$, ,

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $P_{\nu }^{\mu }\left(z\right)$: associated Legendre function of the first kind, $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{e}$: base of natural logarithm, $\mathrm{i}$: imaginary unit, $\mathrm{ph}$: phase, $𝐅(a,b;c;z)$ or $𝐅(\genfrac{}{}{0pt}{}{a,b}{c};z)$: $={}_2{}^{}𝐅_1^{}(a,b;c;z)$ Olver’s hypergeometric function, $z$: complex variable, $a$: real or complex parameter and $b$: real or complex parameter

Permalink:

http://dlmf.nist.gov/15.9.E22

Encodings:

pMML, png, TeX

See also:

Annotations for §15.9(iv), §15.9 and Ch.15

… ►

15.9.23 $$𝐅(\genfrac{}{}{0pt}{}{a,b}{\frac{3}{2}};z)=\frac{2^{a+b-(5/2)}}{\pi \sqrt{z}}\mathrm{\Gamma }\left(a-\frac{1}{2}\right)\mathrm{\Gamma }\left(b-\frac{1}{2}\right){(z-1)}^{(-a-b+(3/2))/2}\left({\mathrm{e}}^{\pm \pi \mathrm{i}(a+b-(3/2))}{P}_{a-b-(1/2)}^{-a-b+(3/2)}\left(-\sqrt{z}\right)-P_{a-b-(1/2)}^{-a-b+(3/2)}\left(\sqrt{z}\right)\right),$$ $a,b\ne \frac{1}{2},-\frac{1}{2},-\frac{3}{2},\mathrm{\dots }$, ,

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $P_{\nu }^{\mu }\left(z\right)$: associated Legendre function of the first kind, $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{e}$: base of natural logarithm, $\mathrm{i}$: imaginary unit, $\mathrm{ph}$: phase, $𝐅(a,b;c;z)$ or $𝐅(\genfrac{}{}{0pt}{}{a,b}{c};z)$: $={}_2{}^{}𝐅_1^{}(a,b;c;z)$ Olver’s hypergeometric function, $z$: complex variable, $a$: real or complex parameter and $b$: real or complex parameter

Permalink:

http://dlmf.nist.gov/15.9.E23

Encodings:

pMML, png, TeX

See also:

Annotations for §15.9(iv), §15.9 and Ch.15

…