DLMF: Untitled Document

… ►

§7.24(i) Approximations in Terms of Elementary Functions

… ►

•

Cody (1969) provides minimax rational approximations for $\operatorname{erf}x$ and $\operatorname{erfc}x$ . The maximum relative precision is about 20S.

►

•

Cody (1968) gives minimax rational approximations for the Fresnel integrals (maximum relative precision 19S); for a Fortran algorithm and comments see Snyder (1993).

►

•

Cody et al. (1970) gives minimax rational approximations to Dawson’s integral $F\left(x\right)$ (maximum relative precision 20S–22S).

… ►

•

Luke (1969b, vol. 2, pp. 422–435) gives main diagonal Padé approximations for $F\left(z\right)$ , $\operatorname{erf}z$ , $\operatorname{erfc}z$ , $C\left(z\right)$ , and $S\left(z\right)$ ; approximate errors are given for a selection of $z$ -values.

… ►The right-hand side is called Clausen’s integral. … ►

Integral Representation

… ►

§25.12(iii) Fermi–Dirac and Bose–Einstein Integrals

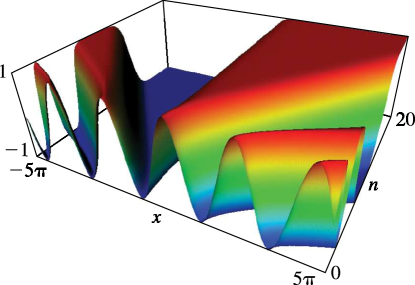
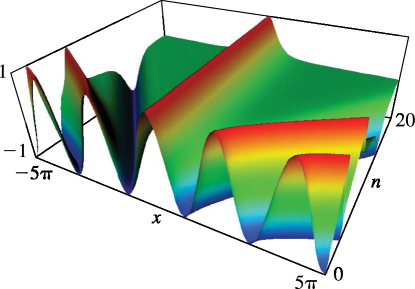
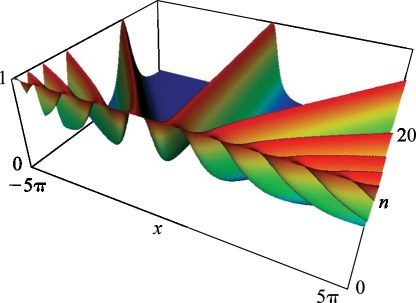
►The Fermi–Dirac and Bose–Einstein integrals are defined by … ►In terms of polylogarithms …

… ►

See accompanying text — Figure 22.3.13: $\operatorname{sn}\left(x,k\right)$ for $k=1-e^{-n}$ , $n=0$ to 20, $-5\pi\leq x\leq 5\pi$ . Magnify 3D Help

►

… ►

…

… ►

•

Achenbach (1986) tabulates $J_{0}\left(x\right)$ , $J_{1}\left(x\right)$ , $Y_{0}\left(x\right)$ , $Y_{1}\left(x\right)$ , $x=0(.1)8$ , 20D or 18–20S.

… ►

•

Zhang and Jin (1996, p. 270) tabulates $\int_{0}^{x}J_{0}\left(t\right)\,\mathrm{d}t$ , $\int_{0}^{x}t^{-1}(1-J_{0}\left(t\right))\,\mathrm{d}t$ , $\int_{0}^{x}Y_{0}\left(t\right)\,\mathrm{d}t$ , $\int_{x}^{\infty}t^{-1}Y_{0}\left(t\right)\,\mathrm{d}t$ , $x=0(.1)1(.5)20$ , 8D.

… ►

•

Bickley et al. (1952) tabulates $x^{-n}I_{n}\left(x\right)$ or $e^{-x}I_{n}\left(x\right)$ , $x^{n}K_{n}\left(x\right)$ or $e^{x}K_{n}\left(x\right)$ , $n=2(1)20$ , $x=0$ (.01 or .1) 10(.1) 20, 8S; $I_{n}\left(x\right)$ , $K_{n}\left(x\right)$ , $n=0(1)20$ , $x=0$ or $0.1(.1)20$ , 10S.

… ►

•

Kerimov and Skorokhodov (1984b) tabulates all zeros of the principal values of $K_{n}\left(z\right)$ and $K_{n}'\left(z\right)$ , for $n=2(1)20$ , 9S.

… ►

•

Zhang and Jin (1996, p. 271) tabulates $e^{-x}\int_{0}^{x}I_{0}\left(t\right)\,\mathrm{d}t$ , $e^{-x}\int_{0}^{x}t^{-1}(I_{0}\left(t\right)-1)\,\mathrm{d}t$ , $e^{x}\int_{x}^{\infty}K_{0}\left(t\right)\,\mathrm{d}t$ , $xe^{x}\int_{x}^{\infty}t^{-1}K_{0}\left(t\right)\,\mathrm{d}t$ , $x=0(.1)1(.5)20$ , 8D.

…

… ►

§6.16(i) The Gibbs Phenomenon

… ►Hence, if

x

is fixed and

n\to\infty

, then

S_{n}(x)\to\frac{1}{4}\pi

,

0

, or

-\frac{1}{4}\pi

according as

0<x<\pi

,

x=0

, or

-\pi<x<0

; compare (6.2.14). … ►The first maximum of

\frac{1}{2}\operatorname{Si}\left(x\right)

for positive

x

occurs at

x=\pi

and equals

(1.1789\dots)\times\frac{1}{4}\pi

; compare Figure 6.3.2. … ►

§6.16(ii) Number-Theoretic Significance of $\operatorname{li}\left(x\right)$

►If we assume Riemann’s hypothesis that all nonreal zeros of

\zeta\left(s\right)

have real part of

\tfrac{1}{2}

(§25.10(i)), then …

… ►

•

Cody et al. (1971) gives rational approximations for $\zeta\left(s\right)$ in the form of quotients of polynomials or quotients of Chebyshev series. The ranges covered are $0.5\leq s\leq 5$ , $5\leq s\leq 11$ , $11\leq s\leq 25$ , $25\leq s\leq 55$ . Precision is varied, with a maximum of 20S.

… ►

•

Morris (1979) gives rational approximations for $\operatorname{Li}_{2}\left(x\right)$ (§25.12(i)) for $0.5\leq x\leq 1$ . Precision is varied with a maximum of 24S.

►

•

Antia (1993) gives minimax rational approximations for $\Gamma\left(s+1\right)F_{s}(x)$ , where $F_{s}(x)$ is the Fermi–Dirac integral (25.12.14), for the intervals $-\infty<x\leq 2$ and $2\leq x<\infty$ , with $s=-\frac{1}{2},\frac{1}{2},\frac{3}{2},\frac{5}{2}$ . For each $s$ there are three sets of approximations, with relative maximum errors $10^{-4},10^{-8},10^{-12}$ .

§23.14 Integrals

►

23.14.1

\int\wp\left(z\right)\,\mathrm{d}z=-\zeta\left(z\right),

ⓘ

Symbols:: $\wp\left(\NVar{z}\right)$ (= $\wp\left(z|\mathbb{L}\right)$ = $\wp\left(z;g_{2},g_{3}\right)$ ): Weierstrass $\wp$ -function, $\zeta\left(\NVar{z}\right)$ (= $\zeta\left(z|\mathbb{L}\right)$ = $\zeta\left(z;g_{2},g_{3}\right)$ ): Weierstrass zeta function, $\,\mathrm{d}\NVar{x}$ : differential of $x$ , $\int$ : integral, $\mathbb{L}$ : lattice and $z$ : complex
A&S Ref:: 18.6.1
Permalink:: http://dlmf.nist.gov/23.14.E1
Encodings:: pMML, png, TeX
See also:: Annotations for §23.14 and Ch.23

►

23.14.2

\int{\wp}^{2}\left(z\right)\,\mathrm{d}z=\frac{1}{6}\wp'\left(z\right)+\frac{1% }{12}g_{2}z,

ⓘ

Symbols:: $\wp\left(\NVar{z}\right)$ (= $\wp\left(z|\mathbb{L}\right)$ = $\wp\left(z;g_{2},g_{3}\right)$ ): Weierstrass $\wp$ -function, $g_{\NVar{j}}$ : Weierstrass lattice invariants $g_{2}$ , $g_{3}$ , $\,\mathrm{d}\NVar{x}$ : differential of $x$ , $\int$ : integral, $\mathbb{L}$ : lattice and $z$ : complex
A&S Ref:: 18.7.1
Permalink:: http://dlmf.nist.gov/23.14.E2
Encodings:: pMML, png, TeX
See also:: Annotations for §23.14 and Ch.23

►

23.14.3

\int{\wp}^{3}\left(z\right)\,\mathrm{d}z=\frac{1}{120}\wp'''\left(z\right)-% \frac{3}{20}g_{2}\zeta\left(z\right)+\frac{1}{10}g_{3}z.

ⓘ

Symbols:: $\wp\left(\NVar{z}\right)$ (= $\wp\left(z|\mathbb{L}\right)$ = $\wp\left(z;g_{2},g_{3}\right)$ ): Weierstrass $\wp$ -function, $g_{\NVar{j}}$ : Weierstrass lattice invariants $g_{2}$ , $g_{3}$ , $\zeta\left(\NVar{z}\right)$ (= $\zeta\left(z|\mathbb{L}\right)$ = $\zeta\left(z;g_{2},g_{3}\right)$ ): Weierstrass zeta function, $\,\mathrm{d}\NVar{x}$ : differential of $x$ , $\int$ : integral, $\mathbb{L}$ : lattice and $z$ : complex
A&S Ref:: 18.7.2
Permalink:: http://dlmf.nist.gov/23.14.E3
Encodings:: pMML, png, TeX
See also:: Annotations for §23.14 and Ch.23

►For further integrals see Gröbner and Hofreiter (1949, Vol. 1, pp. 161–162), Gradshteyn and Ryzhik (2000, p. 622), and Prudnikov et al. (1990, pp. 51–52).

… ►

•

Zhang and Jin (1996, p. 337) tabulates $\operatorname{Ai}\left(x\right)$ , $\operatorname{Ai}'\left(x\right)$ , $\operatorname{Bi}\left(x\right)$ , $\operatorname{Bi}'\left(x\right)$ for $x=0(1)20$ to 8S and for $x=-20(1)0$ to 9D.

… ►

•

Miller (1946) tabulates $a_{k}$ , $\operatorname{Ai}'\left(a_{k}\right)$ , $a^{\prime}_{k}$ , $\operatorname{Ai}\left(a^{\prime}_{k}\right)$ , $k=1(1)50$ ; $b_{k}$ , $\operatorname{Bi}'\left(b_{k}\right)$ , $b^{\prime}_{k}$ , $\operatorname{Bi}\left(b^{\prime}_{k}\right)$ , $k=1(1)20$ . Precision is 8D. Entries for $k=1(1)20$ are reproduced in Abramowitz and Stegun (1964, Chapter 10).

►

•

Sherry (1959) tabulates $a_{k}$ , $\operatorname{Ai}'\left(a_{k}\right)$ , $a^{\prime}_{k}$ , $\operatorname{Ai}\left(a^{\prime}_{k}\right)$ , $k=1(1)50$ ; 20S.

►

•

Zhang and Jin (1996, p. 339) tabulates $a_{k}$ , $\operatorname{Ai}'\left(a_{k}\right)$ , $a^{\prime}_{k}$ , $\operatorname{Ai}\left(a^{\prime}_{k}\right)$ , $b_{k}$ , $\operatorname{Bi}'\left(b_{k}\right)$ , $b^{\prime}_{k}$ , $\operatorname{Bi}\left(b^{\prime}_{k}\right)$ , $k=1(1)20$ ; 8D.

… ►

§9.18(v) Integrals

…

… ►

•

Abramowitz and Stegun (1964, Chapter 7) includes $\operatorname{erf}x$ , $(2/\sqrt{\pi})e^{-x^{2}}$ , $x\in[0,2]$ , 10D; $(2/\sqrt{\pi})e^{-x^{2}}$ , $x\in[2,10]$ , 8S; $xe^{x^{2}}\operatorname{erfc}x$ , $x^{-2}\in[0,0.25]$ , 7D; $2^{n}\Gamma\left(\frac{1}{2}n+1\right)\mathop{\mathrm{i}^{n}\mathrm{erfc}}% \left(x\right)$ , $n=1(1)6,10,11$ , $x\in[0,5]$ , 6S; $F\left(x\right)$ , $x\in[0,2]$ , 10D; $xF\left(x\right)$ , $x^{-2}\in[0,0.25]$ , 9D; $C\left(x\right)$ , $S\left(x\right)$ , $x\in[0,5]$ , 7D; $\mathrm{f}\left(x\right)$ , $\mathrm{g}\left(x\right)$ , $x\in[0,1]$ , $x^{-1}\in[0,1]$ , 15D.

►

•

Abramowitz and Stegun (1964, Table 27.6) includes the Goodwin–Staton integral $G\left(x\right)$ , $x=1(.1)3(.5)8$ , 4D; also $G\left(x\right)+\ln x$ , $x=0(.05)1$ , 4D.

… ►

•

Zhang and Jin (1996, pp. 637, 639) includes $(2/\sqrt{\pi})e^{-x^{2}}$ , $\operatorname{erf}x$ , $x=0(.02)1(.04)3$ , 8D; $C\left(x\right)$ , $S\left(x\right)$ , $x=0(.2)10(2)100(100)500$ , 8D.

… ►

•

Zhang and Jin (1996, pp. 638, 640–641) includes the real and imaginary parts of $\operatorname{erf}z$ , $x\in[0,5]$ , $y=0.5(.5)3$ , 7D and 8D, respectively; the real and imaginary parts of $\int_{x}^{\infty}e^{\pm\mathrm{i}t^{2}}\,\mathrm{d}t$ , $(1/\sqrt{\pi})e^{\mp\mathrm{i}(x^{2}+(\pi/4))}\int_{x}^{\infty}e^{\pm\mathrm{i% }t^{2}}\,\mathrm{d}t$ , $x=0(.5)20(1)25$ , 8D, together with the corresponding modulus and phase to 8D and 6D (degrees), respectively.

… ►

•

Zhang and Jin (1996, p. 642) includes the first 10 zeros of $\operatorname{erf}z$ , 9D; the first 25 distinct zeros of $C\left(z\right)$ and $S\left(z\right)$ , 8S.

… ►

7.8.5

\frac{x^{2}}{2x^{2}+1}\leq\frac{x^{2}(2x^{2}+5)}{4x^{4}+12x^{2}+3}\leq x% \mathsf{M}\left(x\right)<\frac{2x^{4}+9x^{2}+4}{4x^{4}+20x^{2}+15}<\frac{x^{2}% +1}{2x^{2}+3},

x\geq 0

.

ⓘ

Symbols:: $\mathsf{M}\left(\NVar{x}\right)$ : Mills’ ratio and $x$ : real variable
Referenced by:: §7.8
Permalink:: http://dlmf.nist.gov/7.8.E5
Encodings:: pMML, png, TeX
See also:: Annotations for §7.8 and Ch.7

… ►

7.8.6

\int_{0}^{x}e^{at^{2}}\,\mathrm{d}t<\frac{1}{3ax}\left(2e^{ax^{2}}+ax^{2}-2% \right),

a,x>0

.

ⓘ

Symbols:: $\,\mathrm{d}\NVar{x}$ : differential of $x$ , $\mathrm{e}$ : base of natural logarithm, $\int$ : integral and $x$ : real variable
Referenced by:: §7.8
Permalink:: http://dlmf.nist.gov/7.8.E6
Encodings:: pMML, png, TeX
See also:: Annotations for §7.8 and Ch.7

►

7.8.7

\frac{\sinh x^{2}}{x}<{\mathrm{e}}^{x^{2}}F\left(x\right)=\int_{0}^{x}{\mathrm% {e}}^{t^{2}}\,\mathrm{d}t<\frac{{\mathrm{e}}^{x^{2}}-1}{x},

x>0

.

ⓘ

Symbols:: $F\left(\NVar{z}\right)$ : Dawson’s integral, $\,\mathrm{d}\NVar{x}$ : differential of $x$ , $\mathrm{e}$ : base of natural logarithm, $\sinh\NVar{z}$ : hyperbolic sine function, $\int$ : integral and $x$ : real variable
Referenced by:: Erratum (V1.1.5) for Additions
Permalink:: http://dlmf.nist.gov/7.8.E7
Encodings:: pMML, png, TeX
Addition (effective with 1.1.5):: A new inequality was added.
See also:: Annotations for §7.8 and Ch.7

►The function

F\left(x\right)/\sqrt{1-{\mathrm{e}}^{-2x^{2}}}

is strictly decreasing for

x>0

. For these and similar results for Dawson’s integral

F\left(x\right)

see Janssen (2021). …

Heine%20integral

21—30 of 475 matching pages

21: 7.24 Approximations

§7.24(i) Approximations in Terms of Elementary Functions

22: 25.12 Polylogarithms

Integral Representation

§25.12(iii) Fermi–Dirac and Bose–Einstein Integrals

23: 22.3 Graphics

24: 10.75 Tables

25: 6.16 Mathematical Applications

§6.16(i) The Gibbs Phenomenon

§6.16(ii) Number-Theoretic Significance of $\operatorname{li}\left(x\right)$

26: 25.20 Approximations

27: 23.14 Integrals

§23.14 Integrals

28: 9.18 Tables

§9.18(v) Integrals

29: 7.23 Tables

30: 7.8 Inequalities

Heine%20integral

21—30 of 475 matching pages

21: 7.24 Approximations

§7.24(i) Approximations in Terms of Elementary Functions

22: 25.12 Polylogarithms

Integral Representation

§25.12(iii) Fermi–Dirac and Bose–Einstein Integrals

23: 22.3 Graphics

24: 10.75 Tables

25: 6.16 Mathematical Applications

§6.16(i) The Gibbs Phenomenon

§6.16(ii) Number-Theoretic Significance of li ⁡ ( x )

26: 25.20 Approximations

27: 23.14 Integrals

§23.14 Integrals

28: 9.18 Tables

§9.18(v) Integrals

29: 7.23 Tables

30: 7.8 Inequalities

§6.16(ii) Number-Theoretic Significance of $\operatorname{li}\left(x\right)$