������������������������������/������������/������������������CXFK69���epWz5VZ

SearchAdvancedHelp

(0.034 seconds)

31—40 of 676 matching pages

31: 10.8 Power Series

… ►

10.8.1 $$Y_n\left(z\right)=-\frac{{(\frac{1}{2}z)}^{-n}}{\pi }\sum _{k=0}^{n-1}\frac{(n-k-1)!}{k!}{\left(\frac{1}{4}{z}^2\right)}^k+\frac{2}{\pi }\ln \left(\frac{1}{2}z\right)J_n\left(z\right)-\frac{{(\frac{1}{2}z)}^n}{\pi }\sum _{k=0}^{\mathrm{\infty }}(\psi \left(k+1\right)+\psi \left(n+k+1\right))\frac{{(-\frac{1}{4}{z}^2)}^k}{k!(n+k)!},$$

ⓘ

Symbols:

$J_{\nu }\left(z\right)$: Bessel function of the first kind, $Y_{\nu }\left(z\right)$: Bessel function of the second kind, $\pi$: the ratio of the circumference of a circle to its diameter, $\psi \left(z\right)$: psi (or digamma) function, $!$: factorial (as in $n!$), $\ln z$: principal branch of logarithm function, $n$: integer, $k$: nonnegative integer and $z$: complex variable

A&S Ref:

9.1.11

Referenced by:

§10.19(i), §10.7(i)

Permalink:

http://dlmf.nist.gov/10.8.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §10.8 and Ch.10

… ►

10.8.2 $$Y_0\left(z\right)=\frac{2}{\pi }\left(\ln \left(\frac{1}{2}z\right)+\gamma \right)J_0\left(z\right)+\frac{2}{\pi }\left(\frac{\frac{1}{4}{z}^2}{{(1!)}^2}-(1+\frac{1}{2})\frac{{(\frac{1}{4}{z}^2)}^2}{{(2!)}^2}+(1+\frac{1}{2}+\frac{1}{3})\frac{{(\frac{1}{4}{z}^2)}^3}{{(3!)}^2}-\mathrm{\cdots }\right),$$

ⓘ

Symbols:

$J_{\nu }\left(z\right)$: Bessel function of the first kind, $Y_{\nu }\left(z\right)$: Bessel function of the second kind, $\gamma$: Euler’s constant, $\pi$: the ratio of the circumference of a circle to its diameter, $!$: factorial (as in $n!$), $\ln z$: principal branch of logarithm function and $z$: complex variable

A&S Ref:

9.1.13

Referenced by:

§10.22(iii), §10.24, §10.7(i)

Permalink:

http://dlmf.nist.gov/10.8.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §10.8 and Ch.10

… ►

10.8.3 $$J_{\nu }\left(z\right)J_{\mu }\left(z\right)={(\frac{1}{2}z)}^{\nu +\mu }\sum _{k=0}^{\mathrm{\infty }}\frac{{\left(\nu +\mu +k+1\right)}_k{(-\frac{1}{4}{z}^2)}^k}{k!\mathrm{\Gamma }\left(\nu +k+1\right)\mathrm{\Gamma }\left(\mu +k+1\right)}.$$

ⓘ

Symbols:

$J_{\nu }\left(z\right)$: Bessel function of the first kind, $\mathrm{\Gamma }\left(z\right)$: gamma function, ${\left(a\right)}_n$: Pochhammer’s symbol (or shifted factorial), $!$: factorial (as in $n!$), $k$: nonnegative integer, $z$: complex variable and $\nu$: complex parameter

Proof sketch:

Rewrite (16.12.1).

A&S Ref:

9.1.14

Referenced by:

§10.22(ii), §10.31, §10.8, §10.8, §18.17(v), Erratum (V1.0.17) for Section 10.8

Permalink:

http://dlmf.nist.gov/10.8.E3

Encodings:

pMML, png, TeX

Correction (effective with 1.1.2):

The Pochhammer symbol now links to its definition.

See also:

Annotations for §10.8 and Ch.10

…

32: 12.12 Integrals

… ►

12.12.1 $${\int }_0^{\mathrm{\infty }}{\mathrm{e}}^{-\frac{1}{4}{t}^2}{t}^{\mu -1}U(a,t)dt=\frac{\sqrt{\pi }{2}^{-\frac{1}{2}(\mu +a+\frac{1}{2})}\mathrm{\Gamma }\left(\mu \right)}{\mathrm{\Gamma }\left(\frac{1}{2}(\mu +a+\frac{3}{2})\right)},$$ $\mathrm{\Re }\mu >0$ ,

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $\pi$: the ratio of the circumference of a circle to its diameter, $dx$: differential of $x$ , $\mathrm{e}$: base of natural logarithm, $\int$: integral, $U(a,z)$: parabolic cylinder function, $\mathrm{\Re }$: real part and $a$: real or complex parameter

Permalink:

http://dlmf.nist.gov/12.12.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §12.12 and Ch.12

►

12.12.2 $${\int }_0^{\mathrm{\infty }}{\mathrm{e}}^{-\frac{3}{4}{t}^2}{t}^{-a-\frac{3}{2}}U(a,t)dt=2^{\frac{1}{4}+\frac{1}{2}a}\mathrm{\Gamma }\left(-a-\frac{1}{2}\right)\cos \left((\frac{1}{4}a+\frac{1}{8})\pi \right),$$ ,

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $\pi$: the ratio of the circumference of a circle to its diameter, $\cos z$: cosine function, $dx$: differential of $x$ , $\mathrm{e}$: base of natural logarithm, $\int$: integral, $U(a,z)$: parabolic cylinder function, $\mathrm{\Re }$: real part and $a$: real or complex parameter

Permalink:

http://dlmf.nist.gov/12.12.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §12.12 and Ch.12

►

12.12.3 $${\int }_0^{\mathrm{\infty }}{\mathrm{e}}^{-\frac{1}{4}{t}^2}{t}^{-a-\frac{1}{2}}{(x^2+t^2)}^{-1}U(a,t)dt=\sqrt{\pi /2}\mathrm{\Gamma }\left(\frac{1}{2}-a\right)x^{-a-\frac{3}{2}}{\mathrm{e}}^{\frac{1}{4}{x}^2}U(-a,x),$$ .

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $\pi$: the ratio of the circumference of a circle to its diameter, $dx$: differential of $x$ , $\mathrm{e}$: base of natural logarithm, $\int$: integral, $U(a,z)$: parabolic cylinder function, $\mathrm{\Re }$: real part, $x$: real variable and $a$: real or complex parameter

Permalink:

http://dlmf.nist.gov/12.12.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §12.12 and Ch.12

… ►

12.12.4 $${(U(a,z))}^2+{(\overline{U}(a,z))}^2=\frac{2^{\frac{3}{2}}}{\pi }\mathrm{\Gamma }\left(\frac{1}{2}-a\right){\int }_0^{\mathrm{\infty }}\frac{{\mathrm{e}}^{2at+\frac{1}{2}{z}^2\tanh t}}{\sqrt{\sinh \left(2t\right)}}dt,$$ .

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $\pi$: the ratio of the circumference of a circle to its diameter, $dx$: differential of $x$ , $\mathrm{e}$: base of natural logarithm, $\sinh z$: hyperbolic sine function, $\tanh z$: hyperbolic tangent function, $\int$: integral, $U(a,z)$: parabolic cylinder function, $\overline{U}(a,x)$: parabolic cylinder function, $\mathrm{\Re }$: real part, $z$: complex variable and $a$: real or complex parameter

Notes:

See Durand (1975).

Referenced by:

§12.12

Permalink:

http://dlmf.nist.gov/12.12.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §12.12, §12.12 and Ch.12

…

33: 13.19 Asymptotic Expansions for Large Argument

… ►

13.19.1 $$M_{\kappa ,\mu }\left(x\right)\sim \frac{\mathrm{\Gamma }\left(1+2\mu \right)}{\mathrm{\Gamma }\left(\frac{1}{2}+\mu -\kappa \right)}{\mathrm{e}}^{\frac{1}{2}x}{x}^{-\kappa }\sum _{s=0}^{\mathrm{\infty }}\frac{{\left(\frac{1}{2}-\mu +\kappa \right)}_s{\left(\frac{1}{2}+\mu +\kappa \right)}_s}{s!}{x}^{-s},$$ $\mu -\kappa \ne -\frac{1}{2},-\frac{3}{2},\mathrm{\dots }$.

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, ${\left(a\right)}_n$: Pochhammer’s symbol (or shifted factorial), $M_{\kappa ,\mu }\left(z\right)$: Whittaker confluent hypergeometric function, $\sim$: Poincaré asymptotic expansion, $\mathrm{e}$: base of natural logarithm, $!$: factorial (as in $n!$), $s$: nonnegative integer and $x$: real variable

Permalink:

http://dlmf.nist.gov/13.19.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §13.19 and Ch.13

… ►

13.19.2 $$M_{\kappa ,\mu }\left(z\right)\sim \frac{\mathrm{\Gamma }\left(1+2\mu \right)}{\mathrm{\Gamma }\left(\frac{1}{2}+\mu -\kappa \right)}{\mathrm{e}}^{\frac{1}{2}z}{z}^{-\kappa }\sum _{s=0}^{\mathrm{\infty }}\frac{{\left(\frac{1}{2}-\mu +\kappa \right)}_s{\left(\frac{1}{2}+\mu +\kappa \right)}_s}{s!}{z}^{-s}+\frac{\mathrm{\Gamma }\left(1+2\mu \right)}{\mathrm{\Gamma }\left(\frac{1}{2}+\mu +\kappa \right)}{\mathrm{e}}^{-\frac{1}{2}z\pm (\frac{1}{2}+\mu -\kappa )\pi \mathrm{i}}{z}^{\kappa }\sum _{s=0}^{\mathrm{\infty }}\frac{{\left(\frac{1}{2}+\mu -\kappa \right)}_s{\left(\frac{1}{2}-\mu -\kappa \right)}_s}{s!}{(-z)}^{-s},$$ $-\frac{1}{2}\pi +\delta \le \pm \mathrm{ph}z\le \frac{3}{2}\pi -\delta$,

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, ${\left(a\right)}_n$: Pochhammer’s symbol (or shifted factorial), $M_{\kappa ,\mu }\left(z\right)$: Whittaker confluent hypergeometric function, $\sim$: Poincaré asymptotic expansion, $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{e}$: base of natural logarithm, $!$: factorial (as in $n!$), $\mathrm{i}$: imaginary unit, $\mathrm{ph}$: phase, $s$: nonnegative integer, $z$: complex variable and $\delta$: small positive constant

Referenced by:

§13.14(iv)

Permalink:

http://dlmf.nist.gov/13.19.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §13.19 and Ch.13

►provided that both $\mu \mp \kappa \ne -\frac{1}{2},-\frac{3}{2},\mathrm{\dots }$. … ►

13.19.3 $$W_{\kappa ,\mu }\left(z\right)\sim {\mathrm{e}}^{-\frac{1}{2}z}{z}^{\kappa }\sum _{s=0}^{\mathrm{\infty }}\frac{{\left(\frac{1}{2}+\mu -\kappa \right)}_s{\left(\frac{1}{2}-\mu -\kappa \right)}_s}{s!}{(-z)}^{-s},$$ $|\mathrm{ph}z|\le \frac{3}{2}\pi -\delta$.

ⓘ

Symbols:

${\left(a\right)}_n$: Pochhammer’s symbol (or shifted factorial), $W_{\kappa ,\mu }\left(z\right)$: Whittaker confluent hypergeometric function, $\sim$: Poincaré asymptotic expansion, $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{e}$: base of natural logarithm, $!$: factorial (as in $n!$), $\mathrm{ph}$: phase, $s$: nonnegative integer, $z$: complex variable and $\delta$: small positive constant

Referenced by:

§13.14(iv)

Permalink:

http://dlmf.nist.gov/13.19.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §13.19 and Ch.13

…

34: 18.16 Zeros

… ►except when ${\alpha }^2={\beta }^2=\frac{1}{4}$. … ►Then as $n\to \mathrm{\infty }$, with $\alpha$ ($>-\frac{1}{2}$) and $\beta$ ($\ge -1-\alpha$) fixed, … ►when $\alpha \notin (-\frac{1}{2},\frac{1}{2})$. … ►In view of the reflection formula, given in Table 18.6.1, we may consider just the positive zeros $x_{n,m}$, $m=1,2,\mathrm{\dots },\lfloor \frac{1}{2}n\rfloor$. … ►For an asymptotic expansion of $x_{n,m}$ as $n\to \mathrm{\infty }$ that applies uniformly for $m=1,2,\mathrm{\dots },\lfloor \frac{1}{2}n\rfloor$, see Olver (1959, §14(i)). …

35: 15.3 Graphics

… ►

►►

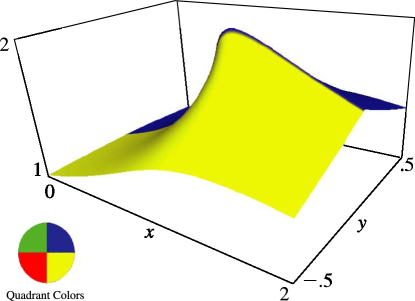
Figure 15.3.1: $F(\frac{4}{3},\frac{9}{16};\frac{14}{5};x),-100\le x\le 1$. Magnify

… ►

►

►

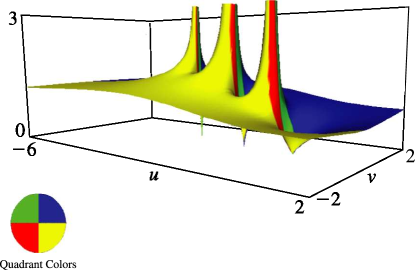
Figure 15.3.5: $F(\frac{4}{3},\frac{9}{16};\frac{14}{5};x+\mathrm{i}y),0\le x\le 2,-0.5\le y\le 0.5$. … Magnify 3D Help

►

►

►

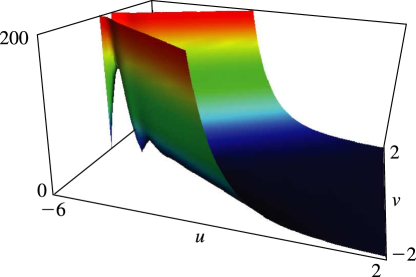
Figure 15.3.6: $F(-3,\frac{3}{5};u+\mathrm{i}v;\frac{1}{2}),-6\le u\le 2,-2\le v\le 2$. … Magnify 3D Help

►

►

►

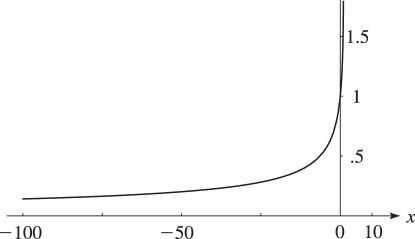
Figure 15.3.7: $|𝐅(-3,\frac{3}{5};u+\mathrm{i}v;\frac{1}{2})|,-6\le u\le 2,-2\le v\le 2$. Magnify 3D Help

36: 10.16 Relations to Other Functions

… ►

$$J_{\frac{1}{2}}\left(z\right)=Y_{-\frac{1}{2}}\left(z\right)={\left(\frac{2}{\pi z}\right)}^{\frac{1}{2}}\sin z,$$

… ►

$$J_{\frac{1}{4}}\left(z\right)=-2^{-\frac{1}{4}}{\pi }^{-\frac{1}{2}}{z}^{-\frac{1}{4}}\left(W(0,2z^{\frac{1}{2}})-W(0,-2z^{\frac{1}{2}})\right),$$

►

$$J_{-\frac{1}{4}}\left(z\right)=2^{-\frac{1}{4}}{\pi }^{-\frac{1}{2}}{z}^{-\frac{1}{4}}\left(W(0,2z^{\frac{1}{2}})+W(0,-2z^{\frac{1}{2}})\right).$$

►

$$J_{\frac{3}{4}}\left(z\right)=-2^{-\frac{1}{4}}{\pi }^{-\frac{1}{2}}{z}^{-\frac{3}{4}}\left(W^{\prime }(0,2z^{\frac{1}{2}})-W^{\prime }(0,-2z^{\frac{1}{2}})\right),$$

… ►In all cases principal branches correspond at least when $|\mathrm{ph}z|\le \frac{1}{2}\pi$. …

37: 4.6 Power Series

… ►

4.6.1 $$\ln \left(1+z\right)=z-\frac{1}{2}{z}^2+\frac{1}{3}{z}^3-\mathrm{\cdots },$$ $|z|\le 1$, $z\ne -1$,

ⓘ

Symbols:

$\ln z$: principal branch of logarithm function and $z$: complex variable

A&S Ref:

4.1.24

Referenced by:

§4.45(i), §4.6(i), (8.15.2)

Permalink:

http://dlmf.nist.gov/4.6.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §4.6(i), §4.6 and Ch.4

►

4.6.2 $$\ln z=\left(\frac{z-1}{z}\right)+\frac{1}{2}{\left(\frac{z-1}{z}\right)}^2+\frac{1}{3}{\left(\frac{z-1}{z}\right)}^3+\mathrm{\cdots },$$ $\mathrm{\Re }z\ge \frac{1}{2}$,

ⓘ

Symbols:

$\ln z$: principal branch of logarithm function, $\mathrm{\Re }$: real part and $z$: complex variable

A&S Ref:

4.1.25

Permalink:

http://dlmf.nist.gov/4.6.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §4.6(i), §4.6 and Ch.4

►

4.6.3 $$\ln z=(z-1)-\frac{1}{2}{(z-1)}^2+\frac{1}{3}{(z-1)}^3-\mathrm{\cdots },$$ $|z-1|\le 1$, $z\ne 0$,

ⓘ

Symbols:

$\ln z$: principal branch of logarithm function and $z$: complex variable

A&S Ref:

4.1.26

Permalink:

http://dlmf.nist.gov/4.6.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §4.6(i), §4.6 and Ch.4

►

4.6.4 $$\ln z=2\left(\left(\frac{z-1}{z+1}\right)+\frac{1}{3}{\left(\frac{z-1}{z+1}\right)}^3+\frac{1}{5}{\left(\frac{z-1}{z+1}\right)}^5+\mathrm{\cdots }\right),$$ $\mathrm{\Re }z\ge 0$, $z\ne 0$,

ⓘ

Symbols:

$\ln z$: principal branch of logarithm function, $\mathrm{\Re }$: real part and $z$: complex variable

A&S Ref:

4.1.27

Permalink:

http://dlmf.nist.gov/4.6.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §4.6(i), §4.6 and Ch.4

… ►

4.6.6 $$\ln \left(z+a\right)=\ln a+2\left(\left(\frac{z}{2a+z}\right)+\frac{1}{3}{\left(\frac{z}{2a+z}\right)}^3+\frac{1}{5}{\left(\frac{z}{2a+z}\right)}^5+\mathrm{\cdots }\right),$$ $a>0$, $\mathrm{\Re }z\ge -a$, $z\ne -a$.

ⓘ

Symbols:

$\ln z$: principal branch of logarithm function, $\mathrm{\Re }$: real part, $a$: real or complex constant and $z$: complex variable

A&S Ref:

4.1.29

Permalink:

http://dlmf.nist.gov/4.6.E6

Encodings:

pMML, png, TeX

See also:

Annotations for §4.6(i), §4.6 and Ch.4

…

38: 12.8 Recurrence Relations and Derivatives

… ►

12.8.2 $$U^{\prime }(a,z)+\frac{1}{2}zU(a,z)+(a+\frac{1}{2})U(a+1,z)=0,$$

ⓘ

Symbols:

$U(a,z)$: parabolic cylinder function, $z$: complex variable and $a$: real or complex parameter

A&S Ref:

19.6.1

Permalink:

http://dlmf.nist.gov/12.8.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §12.8(i), §12.8 and Ch.12

… ►

12.8.6 $$V^{\prime }(a,z)-\frac{1}{2}zV(a,z)-(a-\frac{1}{2})V(a-1,z)=0,$$

ⓘ

Symbols:

$V(a,z)$: parabolic cylinder function, $z$: complex variable and $a$: real or complex parameter

A&S Ref:

19.6.5

Permalink:

http://dlmf.nist.gov/12.8.E6

Encodings:

pMML, png, TeX

See also:

Annotations for §12.8(i), §12.8 and Ch.12

… ►

12.8.9 $$\frac{d^m}{{dz}^m}\left({\mathrm{e}}^{\frac{1}{4}{z}^2}U(a,z)\right)={(-1)}^m{\left(\frac{1}{2}+a\right)}_m{\mathrm{e}}^{\frac{1}{4}{z}^2}U(a+m,z),$$

ⓘ

Symbols:

${\left(a\right)}_n$: Pochhammer’s symbol (or shifted factorial), $\frac{df}{dx}$: derivative of $f$ with respect to $x$ , $\mathrm{e}$: base of natural logarithm, $U(a,z)$: parabolic cylinder function, $z$: complex variable and $a$: real or complex parameter

Referenced by:

§12.8(ii)

Permalink:

http://dlmf.nist.gov/12.8.E9

Encodings:

pMML, png, TeX

See also:

Annotations for §12.8(ii), §12.8 and Ch.12

►

12.8.10 $$\frac{d^m}{{dz}^m}\left({\mathrm{e}}^{-\frac{1}{4}{z}^2}U(a,z)\right)={(-1)}^m{\mathrm{e}}^{-\frac{1}{4}{z}^2}U(a-m,z),$$

ⓘ

Symbols:

$\frac{df}{dx}$: derivative of $f$ with respect to $x$ , $\mathrm{e}$: base of natural logarithm, $U(a,z)$: parabolic cylinder function, $z$: complex variable and $a$: real or complex parameter

Referenced by:

§12.8(ii)

Permalink:

http://dlmf.nist.gov/12.8.E10

Encodings:

pMML, png, TeX

See also:

Annotations for §12.8(ii), §12.8 and Ch.12

►

12.8.11 $$\frac{d^m}{{dz}^m}\left({\mathrm{e}}^{\frac{1}{4}{z}^2}V(a,z)\right)={\mathrm{e}}^{\frac{1}{4}{z}^2}V(a+m,z),$$

ⓘ

Symbols:

$\frac{df}{dx}$: derivative of $f$ with respect to $x$ , $\mathrm{e}$: base of natural logarithm, $V(a,z)$: parabolic cylinder function, $z$: complex variable and $a$: real or complex parameter

Referenced by:

§12.8(ii)

Permalink:

http://dlmf.nist.gov/12.8.E11

Encodings:

pMML, png, TeX

See also:

Annotations for §12.8(ii), §12.8 and Ch.12

…

39: 18.31 Bernstein–Szegő Polynomials

… ►The Bernstein–Szegő polynomials $\{p_n(x)\}$, $n=0,1,\mathrm{\dots }$, are orthogonal on $(-1,1)$ with respect to three types of weight function: ${(1-x^2)}^{-\frac{1}{2}}{(\rho (x))}^{-1}$, ${(1-x^2)}^{\frac{1}{2}}{(\rho (x))}^{-1}$, ${(1-x)}^{\frac{1}{2}}{(1+x)}^{-\frac{1}{2}}{(\rho (x))}^{-1}$. …

40: 16.6 Transformations of Variable

… ►

16.6.1 $${}_3{}^{}F_2^{}(\genfrac{}{}{0pt}{}{a,b,c}{a-b+1,a-c+1};z)={(1-z)}^{-a}{}_3{}^{}F_2^{}(\genfrac{}{}{0pt}{}{a-b-c+1,\frac{1}{2}a,\frac{1}{2}(a+1)}{a-b+1,a-c+1};\frac{-4z}{{(1-z)}^2}).$$

ⓘ

Symbols:

${}_p{}^{}F_q^{}(a_1,\mathrm{\dots },a_p;b_1,\mathrm{\dots },b_q;z)$ or ${}_p{}^{}F_q^{}(\genfrac{}{}{0pt}{}{a_1,\mathrm{\dots },a_p}{b_1,\mathrm{\dots },b_q};z)$: alternatively ${}_p{}^{}F_q^{}(𝐚;𝐛;z)$ or ${}_p{}^{}F_q^{}(\genfrac{}{}{0pt}{}{𝐚}{𝐛};z)$
generalized hypergeometric function, $z$: complex variable, $a,a_1,\mathrm{\dots },a_p$: real or complex parameters and $b,b_1,\mathrm{\dots },b_q$: real or complex parameters

Referenced by:

§16.6

Permalink:

http://dlmf.nist.gov/16.6.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §16.6, §16.6 and Ch.16

… ►

16.6.2 $${}_3{}^{}F_2^{}(\genfrac{}{}{0pt}{}{a,2b-a-1,2-2b+a}{b,a-b+\frac{3}{2}};\frac{z}{4})={(1-z)}^{-a}{}_3{}^{}F_2^{}(\genfrac{}{}{0pt}{}{\frac{1}{3}a,\frac{1}{3}a+\frac{1}{3},\frac{1}{3}a+\frac{2}{3}}{b,a-b+\frac{3}{2}};\frac{-27z}{4{(1-z)}^3}).$$

ⓘ

Symbols:

${}_p{}^{}F_q^{}(a_1,\mathrm{\dots },a_p;b_1,\mathrm{\dots },b_q;z)$ or ${}_p{}^{}F_q^{}(\genfrac{}{}{0pt}{}{a_1,\mathrm{\dots },a_p}{b_1,\mathrm{\dots },b_q};z)$: alternatively ${}_p{}^{}F_q^{}(𝐚;𝐛;z)$ or ${}_p{}^{}F_q^{}(\genfrac{}{}{0pt}{}{𝐚}{𝐛};z)$
generalized hypergeometric function, $z$: complex variable, $a,a_1,\mathrm{\dots },a_p$: real or complex parameters and $b,b_1,\mathrm{\dots },b_q$: real or complex parameters

Referenced by:

§16.6

Permalink:

http://dlmf.nist.gov/16.6.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §16.6, §16.6 and Ch.16

…