§5.9 Integral Representations

Keywords:: gamma function
Permalink:: http://dlmf.nist.gov/5.9

§5.9(i) Gamma Function
§5.9(ii) Psi Function, Euler’s Constant, and Derivatives

§5.9(i) Gamma Function

Notes:: For (5.9.1)–(5.9.2) see Olver (1997b, pp. 37–38). (5.9.3) follows from (5.2.1) by a change of variables. For (5.9.4)–(5.9.7), see Temme (1996b, pp. 43–45 and 77). (5.9.8) and (5.9.9) follow from (5.9.6) and (5.9.7). For (5.9.10) and (5.9.11) see Whittaker and Watson (1927, pp. 251 and 277).
Permalink:: http://dlmf.nist.gov/5.9.i

5.9.1 $\frac{1}{\mu}\mathop{\Gamma\/}\nolimits\!\left(\frac{\nu}{\mu}\right)\frac{1}{z^{{\nu/\mu}}}=\int _{0}^{\infty}\mathop{\exp\/}\nolimits\!\left(-zt^{\mu}\right)t^{{\nu-1}}dt,$

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, $dx$ : differential of $x$ , $\mathop{\exp\/}\nolimits z$ : exponential function, $\int$ : integral and $z$ : complex variable
Referenced by:: §36.2(ii), §4.10(ii), §5.9(i)
Permalink:: http://dlmf.nist.gov/5.9.E1
Encodings:: TeX, pMML, png

$\realpart{\nu}>0$ , $\mu>0$ , and $\realpart{z}>0$ . (The fractional powers have their principal values.)

¶ Hankel’s Loop Integral

Keywords:: Hankel’s loop integral, gamma function

5.9.2 $\frac{1}{\mathop{\Gamma\/}\nolimits\!\left(z\right)}=\frac{1}{2\pi i}\int _{{-\infty}}^{{(0+)}}e^{t}t^{{-z}}dt,$

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, $dx$ : differential of $x$ , $e$ : base of exponential function, $\int$ : integral and $z$ : complex variable
A&S Ref:: 6.1.4 (in a slightly different form.)
Referenced by:: §5.21, §5.9(i)
Permalink:: http://dlmf.nist.gov/5.9.E2
Encodings:: TeX, pMML, png

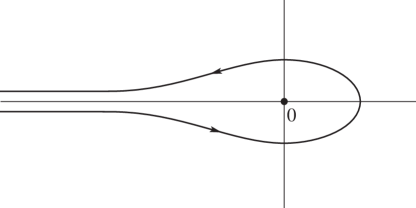
where the contour begins at $-\infty$ , circles the origin once in the positive direction, and returns to $-\infty$ . $t^{{-z}}$ has its principal value where $t$ crosses the positive real axis, and is continuous. See Figure 5.9.1.

Figure 5.9.1: $t$ -plane. Contour for Hankel’s loop integral.

Referenced by:: ¶ ‣ §5.9(i)
Permalink:: http://dlmf.nist.gov/5.9.F1
Encodings:: pdf, png

5.9.3 $c^{{-z}}\mathop{\Gamma\/}\nolimits\!\left(z\right)=\int _{{-\infty}}^{\infty}|t|^{{2z-1}}e^{{-ct^{2}}}dt,$ $c>0$ , $\realpart{z}>0$ ,

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, $dx$ : differential of $x$ , $e$ : base of exponential function, $\int$ : integral, $\realpart{}$ : real part and $z$ : complex variable
Referenced by:: §5.9(i)
Permalink:: http://dlmf.nist.gov/5.9.E3
Encodings:: TeX, pMML, png

where the path is the real axis.

5.9.4 $\mathop{\Gamma\/}\nolimits\!\left(z\right)=\int _{1}^{\infty}t^{{z-1}}e^{{-t}}dt+\sum _{{k=0}}^{\infty}\frac{(-1)^{k}}{(z+k)k!},$ $z\neq 0,-1,-2,\dots$ .

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, $dx$ : differential of $x$ , $e$ : base of exponential function, $!$ : $n!$ : factorial, $\int$ : integral, $k$ : nonnegative integer and $z$ : complex variable
Referenced by:: §5.9(i)
Permalink:: http://dlmf.nist.gov/5.9.E4
Encodings:: TeX, pMML, png

5.9.5 $\mathop{\Gamma\/}\nolimits\!\left(z\right)=\int _{0}^{\infty}t^{{z-1}}\left(e^{{-t}}-\sum _{{k=0}}^{n}\frac{(-1)^{k}t^{k}}{k!}\right)dt,$ $-n-1<\realpart{z}<-n$ .

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, $dx$ : differential of $x$ , $e$ : base of exponential function, $!$ : $n!$ : factorial, $\int$ : integral, $\realpart{}$ : real part, $n$ : nonnegative integer, $k$ : nonnegative integer and $z$ : complex variable
Permalink:: http://dlmf.nist.gov/5.9.E5
Encodings:: TeX, pMML, png

5.9.6 $\mathop{\Gamma\/}\nolimits\!\left(z\right)\mathop{\cos\/}\nolimits\!\left(\tfrac{1}{2}\pi z\right)=\int _{0}^{\infty}t^{{z-1}}\mathop{\cos\/}\nolimits tdt,$ $0<\realpart{z}<1$ ,

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, $\mathop{\cos\/}\nolimits z$ : cosine function, $dx$ : differential of $x$ , $\int$ : integral, $\realpart{}$ : real part and $z$ : complex variable
Referenced by:: §5.9(i)
Permalink:: http://dlmf.nist.gov/5.9.E6
Encodings:: TeX, pMML, png

5.9.7 $\mathop{\Gamma\/}\nolimits\!\left(z\right)\mathop{\sin\/}\nolimits\!\left(\tfrac{1}{2}\pi z\right)=\int _{0}^{\infty}t^{{z-1}}\mathop{\sin\/}\nolimits tdt,$ $-1<\realpart{z}<1$ .

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, $dx$ : differential of $x$ , $\int$ : integral, $\realpart{}$ : real part, $\mathop{\sin\/}\nolimits z$ : sine function and $z$ : complex variable
Referenced by:: §5.9(i)
Permalink:: http://dlmf.nist.gov/5.9.E7
Encodings:: TeX, pMML, png

5.9.8 $\mathop{\Gamma\/}\nolimits\!\left(1+\frac{1}{n}\right)\mathop{\cos\/}\nolimits\!\left(\frac{\pi}{2n}\right)=\int _{0}^{\infty}\mathop{\cos\/}\nolimits\!\left(t^{n}\right)dt,$ $n=2,3,4,\dots$ ,

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, $\mathop{\cos\/}\nolimits z$ : cosine function, $dx$ : differential of $x$ , $\int$ : integral and $n$ : nonnegative integer
Referenced by:: §5.9(i)
Permalink:: http://dlmf.nist.gov/5.9.E8
Encodings:: TeX, pMML, png

5.9.9 $\mathop{\Gamma\/}\nolimits\!\left(1+\frac{1}{n}\right)\mathop{\sin\/}\nolimits\!\left(\frac{\pi}{2n}\right)=\int _{0}^{\infty}\mathop{\sin\/}\nolimits\!\left(t^{n}\right)dt,$ $n=2,3,4,\dots$ .

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, $dx$ : differential of $x$ , $\int$ : integral, $\mathop{\sin\/}\nolimits z$ : sine function and $n$ : nonnegative integer
Referenced by:: §5.9(i)
Permalink:: http://dlmf.nist.gov/5.9.E9
Encodings:: TeX, pMML, png

¶ Binet’s Formula

Keywords:: Binet’s formula, gamma function

5.9.10 $\mathop{\ln\/}\nolimits\mathop{\Gamma\/}\nolimits\!\left(z\right)=\left(z-\tfrac{1}{2}\right)\mathop{\ln\/}\nolimits z-z+\tfrac{1}{2}\mathop{\ln\/}\nolimits\!\left(2\pi\right)+2\int _{0}^{\infty}\frac{\mathop{\mathrm{arctan}\/}\nolimits\!\left(t/z\right)}{e^{{2\pi t}}-1}dt,$

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, $dx$ : differential of $x$ , $e$ : base of exponential function, $\int$ : integral, $\mathop{\mathrm{arctan}\/}\nolimits z$ : arctangent function, $\mathop{\ln\/}\nolimits z$ : principal branch of logarithm function and $z$ : complex variable
A&S Ref:: 6.1.50
Referenced by:: §5.9(i), §5.9(ii)
Permalink:: http://dlmf.nist.gov/5.9.E10
Encodings:: TeX, pMML, png

where $|\mathop{\mathrm{ph}\/}\nolimits z|<\pi/2$ and the inverse tangent has its principal value.

5.9.11 $\mathop{\ln\/}\nolimits\mathop{\Gamma\/}\nolimits\!\left(z+1\right)=-\EulerConstant z-\frac{1}{2\pi i}\int _{{-c-\infty i}}^{{-c+\infty i}}\frac{\pi z^{{-s}}}{s\mathop{\sin\/}\nolimits\!\left(\pi s\right)}\mathop{\zeta\/}\nolimits\!\left(-s\right)ds,$

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, $\EulerConstant$ : Euler’s constant, $\mathop{\zeta\/}\nolimits\!\left(s\right)$ : Riemann zeta function, $dx$ : differential of $x$ , $\int$ : integral, $\mathop{\ln\/}\nolimits z$ : principal branch of logarithm function, $\mathop{\sin\/}\nolimits z$ : sine function, $s$ : real or complex variable and $z$ : complex variable
Referenced by:: §5.9(i), §5.9(ii)
Permalink:: http://dlmf.nist.gov/5.9.E11
Encodings:: TeX, pMML, png

where $|\mathop{\mathrm{ph}\/}\nolimits z|\leq\pi-\delta$ ( $<\pi$ ), $1<c<2$ , and $\mathop{\zeta\/}\nolimits\!\left(s\right)$ is as in Chapter 25.

For additional representations see Whittaker and Watson (1927, §§12.31–12.32).

§5.9(ii) Psi Function, Euler’s Constant, and Derivatives

Notes:: See Olver (1997b, pp. 39–40), Temme (1996b, pp. 55–56), and Whittaker and Watson (1927, pp. 246–251). (5.9.15) and (5.9.17) are the differentiated forms of (5.9.10) and (5.9.11). (5.9.19) is the differentiated form of (5.2.1).
Keywords:: Euler’s constant, gamma function, psi function
Permalink:: http://dlmf.nist.gov/5.9.ii

For $\realpart{z}>0$ ,

5.9.12 $\mathop{\psi\/}\nolimits\!\left(z\right)=\int _{0}^{\infty}\left(\frac{e^{{-t}}}{t}-\frac{e^{{-zt}}}{1-e^{{-t}}}\right)dt,$

Symbols:: $dx$ : differential of $x$ , $\mathop{\psi\/}\nolimits\!\left(z\right)$ : psi (or digamma) function, $e$ : base of exponential function, $\int$ : integral and $z$ : complex variable
A&S Ref:: 6.3.21
Permalink:: http://dlmf.nist.gov/5.9.E12
Encodings:: TeX, pMML, png

5.9.13 $\mathop{\psi\/}\nolimits\!\left(z\right)=\mathop{\ln\/}\nolimits z+\int _{0}^{\infty}\left(\frac{1}{t}-\frac{1}{1-e^{{-t}}}\right)e^{{-tz}}dt,$

Symbols:: $dx$ : differential of $x$ , $\mathop{\psi\/}\nolimits\!\left(z\right)$ : psi (or digamma) function, $e$ : base of exponential function, $\int$ : integral, $\mathop{\ln\/}\nolimits z$ : principal branch of logarithm function and $z$ : complex variable
Permalink:: http://dlmf.nist.gov/5.9.E13
Encodings:: TeX, pMML, png

5.9.14 $\mathop{\psi\/}\nolimits\!\left(z\right)=\int _{0}^{\infty}\left(e^{{-t}}-\frac{1}{(1+t)^{z}}\right)\frac{dt}{t},$

Symbols:: $dx$ : differential of $x$ , $\mathop{\psi\/}\nolimits\!\left(z\right)$ : psi (or digamma) function, $e$ : base of exponential function, $\int$ : integral and $z$ : complex variable
A&S Ref:: 6.3.21
Permalink:: http://dlmf.nist.gov/5.9.E14
Encodings:: TeX, pMML, png

5.9.15 $\mathop{\psi\/}\nolimits\!\left(z\right)=\mathop{\ln\/}\nolimits z-\frac{1}{2z}-2\int _{0}^{\infty}\frac{tdt}{(t^{2}+z^{2})(e^{{2\pi t}}-1)}.$

Symbols:: $dx$ : differential of $x$ , $\mathop{\psi\/}\nolimits\!\left(z\right)$ : psi (or digamma) function, $e$ : base of exponential function, $\int$ : integral, $\mathop{\ln\/}\nolimits z$ : principal branch of logarithm function and $z$ : complex variable
A&S Ref:: 6.3.21
Referenced by:: §5.9(ii)
Permalink:: http://dlmf.nist.gov/5.9.E15
Encodings:: TeX, pMML, png

5.9.16 $\mathop{\psi\/}\nolimits\!\left(z\right)+\EulerConstant=\int _{0}^{\infty}\frac{e^{{-t}}-e^{{-zt}}}{1-e^{{-t}}}dt=\int _{0}^{1}\frac{1-t^{{z-1}}}{1-t}dt.$

Symbols:: $\EulerConstant$ : Euler’s constant, $dx$ : differential of $x$ , $\mathop{\psi\/}\nolimits\!\left(z\right)$ : psi (or digamma) function, $e$ : base of exponential function, $\int$ : integral and $z$ : complex variable
A&S Ref:: 6.3.22
Permalink:: http://dlmf.nist.gov/5.9.E16
Encodings:: TeX, pMML, png

5.9.17 $\mathop{\psi\/}\nolimits\!\left(z+1\right)=-\EulerConstant+\frac{1}{2\pi i}\int _{{-c-\infty i}}^{{-c+\infty i}}\frac{\pi z^{{-s-1}}}{\mathop{\sin\/}\nolimits\!\left(\pi s\right)}\mathop{\zeta\/}\nolimits\!\left(-s\right)ds,$

Symbols:: $\EulerConstant$ : Euler’s constant, $\mathop{\zeta\/}\nolimits\!\left(s\right)$ : Riemann zeta function, $dx$ : differential of $x$ , $\mathop{\psi\/}\nolimits\!\left(z\right)$ : psi (or digamma) function, $\int$ : integral, $\mathop{\sin\/}\nolimits z$ : sine function, $s$ : real or complex variable and $z$ : complex variable
Referenced by:: §5.9(ii)
Permalink:: http://dlmf.nist.gov/5.9.E17
Encodings:: TeX, pMML, png

where $|\mathop{\mathrm{ph}\/}\nolimits z|\leq\pi-\delta(<\pi)$ and $1<c<2$ .

5.9.18 $\EulerConstant=-\int _{0}^{\infty}e^{{-t}}\mathop{\ln\/}\nolimits tdt=\int _{0}^{\infty}\left(\frac{1}{1+t}-e^{{-t}}\right)\frac{dt}{t}=\int _{0}^{1}(1-e^{{-t}})\frac{dt}{t}-\int _{1}^{\infty}e^{{-t}}\frac{dt}{t}=\int _{0}^{\infty}\left(\frac{e^{{-t}}}{1-e^{{-t}}}-\frac{e^{{-t}}}{t}\right)dt.$

Symbols:: $\EulerConstant$ : Euler’s constant, $dx$ : differential of $x$ , $e$ : base of exponential function, $\int$ : integral and $\mathop{\ln\/}\nolimits z$ : principal branch of logarithm function
A&S Ref:: 6.3.22
Referenced by:: §9.12(viii)
Permalink:: http://dlmf.nist.gov/5.9.E18
Encodings:: TeX, pMML, png

5.9.19 ${\mathop{\Gamma\/}\nolimits^{{(n)}}}\!\left(z\right)=\int _{0}^{\infty}(\mathop{\ln\/}\nolimits t)^{n}e^{{-t}}t^{{z-1}}dt,$ $n\geq 0$ , $\realpart{z}>0$ .

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, $dx$ : differential of $x$ , $e$ : base of exponential function, $\int$ : integral, $\mathop{\ln\/}\nolimits z$ : principal branch of logarithm function, $\realpart{}$ : real part, $n$ : nonnegative integer and $z$ : complex variable
Referenced by:: §5.9(ii)
Permalink:: http://dlmf.nist.gov/5.9.E19
Encodings:: TeX, pMML, png

§5.9 Integral Representations

Contents

§5.9(i) Gamma Function

¶ Hankel’s Loop Integral

¶ Binet’s Formula

§5.9(ii) Psi Function, Euler’s Constant, and Derivatives