gamma function

SearchAdvancedHelp

(0.006 seconds)

1—10 of 356 matching pages

1: 8.23 Statistical Applications

§8.23 Statistical Applications

►The functions $P(a,x)$ and $Q(a,x)$ are used extensively in statistics as the probability integrals of the gamma distribution; see Johnson et al. (1994, pp. 337–414). …In queueing theory the Erlang loss function is used, which can be expressed in terms of the reciprocal of $Q(a,x)$; see Jagerman (1974) and Cooper (1981, pp. 80, 316–319).

2: 8.16 Generalizations

§8.16 Generalizations

►For a generalization of the incomplete gamma function, including asymptotic approximations, see Chaudhry and Zubair (1994, 2001) and Chaudhry et al. (1996). …

3: 8.24 Physical Applications

§8.24 Physical Applications

►

§8.24(i) Incomplete Gamma Functions

►The function $\gamma (a,x)$ appears in: discussions of power-law relaxation times in complex physical systems (Sornette (1998)); logarithmic oscillations in relaxation times for proteins (Metzler et al. (1999)); Gaussian orbitals and exponential (Slater) orbitals in quantum chemistry (Shavitt (1963), Shavitt and Karplus (1965)); population biology and ecological systems (Camacho et al. (2002)). …

4: 5.3 Graphics

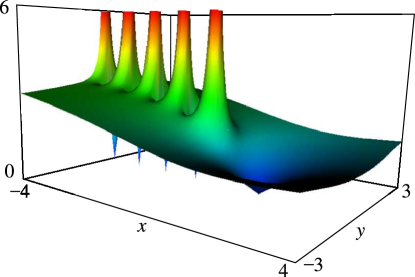
§5.3 Graphics

… ►

►►

Figure 5.3.1: $\mathrm{\Gamma }\left(x\right)$ and $1/\mathrm{\Gamma }\left(x\right)$. … Magnify

►

►►

Figure 5.3.2: $\ln \mathrm{\Gamma }\left(x\right)$. … Magnify

… ►

►

►

Figure 5.3.5: $1/|\mathrm{\Gamma }\left(x+\mathrm{i}y\right)|$. Magnify 3D Help

►

►

►

Figure 5.3.6: $|\psi \left(x+\mathrm{i}y\right)|$. Magnify 3D Help

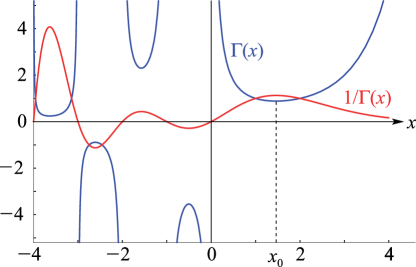5: 8.2 Definitions and Basic Properties

§8.2 Definitions and Basic Properties

… ►The general values of the incomplete gamma functions $\gamma (a,z)$ and $\mathrm{\Gamma }(a,z)$ are defined by … ►

§8.2(ii) Analytic Continuation

►In this subsection the functions $\gamma$ and $\mathrm{\Gamma }$ have their general values. … ►

§8.2(iii) Differential Equations

…

6: 8.22 Mathematical Applications

§8.22 Mathematical Applications

►

§8.22(i) Terminant Function

… ►

§8.22(ii) Riemann Zeta Function and Incomplete Riemann Zeta Function

►The function $\mathrm{\Gamma }(a,z)$, with $|\mathrm{ph}a|\le \frac{1}{2}\pi$ and $\mathrm{ph}z=\frac{1}{2}\pi$, has an intimate connection with the Riemann zeta function $\zeta \left(s\right)$ (§25.2(i)) on the critical line $\mathrm{\Re }s=\frac{1}{2}$. See Paris and Cang (1997). …

7: 5 Gamma Function

Chapter 5 Gamma Function

…

8: 5.1 Special Notation

… ► ►►

$j,m,n$	nonnegative integers.
…

►The main functions treated in this chapter are the gamma function $\mathrm{\Gamma }\left(z\right)$, the psi function (or digamma function) $\psi \left(z\right)$, the beta function $\mathrm{B}(a,b)$, and the $q$-gamma function ${\mathrm{\Gamma }}_q\left(z\right)$. … ►Alternative notations for this function are: $\mathrm{\Pi }(z-1)$ (Gauss) and $(z-1)!$. …

9: 5.5 Functional Relations

… ►

§5.5(i) Recurrence

… ►

§5.5(ii) Reflection

… ►

§5.5(iii) Multiplication

►

Duplication Formula

… ►

§5.5(iv) Bohr–Mollerup Theorem

…

10: 8.7 Series Expansions

§8.7 Series Expansions

… ►

8.7.2 $$\gamma (a,x+y)-\gamma (a,x)=\mathrm{\Gamma }(a,x)-\mathrm{\Gamma }(a,x+y)={\mathrm{e}}^{-x}{x}^{a-1}\sum _{n=0}^{\mathrm{\infty }}\frac{{\left(1-a\right)}_n}{{(-x)}^n}(1-{\mathrm{e}}^{-y}{e}_n(y)),$$ .

ⓘ

Symbols:

${\left(a\right)}_n$: Pochhammer’s symbol (or shifted factorial), $\mathrm{e}$: base of natural logarithm, $\mathrm{\Gamma }(a,z)$: incomplete gamma function, $\gamma (a,z)$: incomplete gamma function, $x$: real variable, $a$: parameter, $n$: nonnegative integer and $e_n(z)$: functions

A&S Ref:

6.5.30

Permalink:

http://dlmf.nist.gov/8.7.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §8.7 and Ch.8

►

8.7.3 $$\mathrm{\Gamma }(a,z)=\mathrm{\Gamma }\left(a\right)-\sum _{k=0}^{\mathrm{\infty }}\frac{{(-1)}^k{z}^{a+k}}{k!(a+k)}=\mathrm{\Gamma }\left(a\right)\left(1-z^a{\mathrm{e}}^{-z}\sum _{k=0}^{\mathrm{\infty }}\frac{z^k}{\mathrm{\Gamma }\left(a+k+1\right)}\right),$$ $a\ne 0,-1,-2,\mathrm{\dots }$.

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $\mathrm{e}$: base of natural logarithm, $!$: factorial (as in $n!$), $\mathrm{\Gamma }(a,z)$: incomplete gamma function, $z$: complex variable, $a$: parameter and $k$: nonnegative integer

Referenced by:

§8.14, §8.19(iv), §8.4, §8.7

Permalink:

http://dlmf.nist.gov/8.7.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §8.7 and Ch.8

►

8.7.4 $$\gamma (a,x)=\mathrm{\Gamma }\left(a\right)x^{\frac{1}{2}a}{\mathrm{e}}^{-x}\sum _{n=0}^{\mathrm{\infty }}{e}_n(-1)x^{\frac{1}{2}n}{I}_{n+a}\left(2x^{1/2}\right),$$ $a\ne 0,-1,-2,\mathrm{\dots }$.

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $\mathrm{e}$: base of natural logarithm, $\gamma (a,z)$: incomplete gamma function, $I_{\nu }\left(z\right)$: modified Bessel function of the first kind, $x$: real variable, $a$: parameter, $n$: nonnegative integer and $e_n(z)$: functions

Permalink:

http://dlmf.nist.gov/8.7.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §8.7 and Ch.8

… ►For an expansion for $\gamma (a,\mathrm{i}x)$ in series of Bessel functions $J_n\left(x\right)$ that converges rapidly when $a>0$ and $x$ ($\ge 0$) is small or moderate in magnitude see Barakat (1961).