12 Parabolic Cylinder Functions Properties 12.13 Sums 12.15 Generalized Parabolic Cylinder Functions

§12.14 The Function $\mathop{W\/}\nolimits\!\left(a,x\right)$

Keywords:: parabolic cylinder functions
Referenced by:: §12.2(i)
Permalink:: http://dlmf.nist.gov/12.14

§12.14(i) Introduction
§12.14(ii) Values at and Wronskian
§12.14(iii) Graphs
§12.14(iv) Connection Formula
§12.14(v) Power-Series Expansions
§12.14(vi) Integral Representations
§12.14(vii) Relations to Other Functions
§12.14(viii) Asymptotic Expansions for Large Variable
§12.14(ix) Uniform Asymptotic Expansions for Large Parameter
§12.14(x) Modulus and Phase Functions
§12.14(xi) Zeros of $\mathop{W\/}\nolimits\!\left(a,x\right)$ , ${\mathop{W\/}\nolimits^{{\prime}}}\!\left(a,x\right)$

§12.14(i) Introduction

Notes:: See Miller (1955, pp. 17–18) and Miller (1952).
Defines:: $\mathop{W\/}\nolimits\!\left(a,x\right)$ : parabolic cylinder function
Keywords:: differential equations, parabolic cylinder functions
Referenced by:: ¶ ‣ §10.16
Permalink:: http://dlmf.nist.gov/12.14.i

In this section solutions of equation (12.2.3) are considered. This equation is important when and are real, and we shall assume this to be the case. In other cases the general theory of (12.2.2) is available. $\mathop{W\/}\nolimits\!\left(a,x\right)$ and $\mathop{W\/}\nolimits\!\left(a,-x\right)$ form a numerically satisfactory pair of solutions when $-\infty<x<\infty$ .

§12.14(ii) Values at and Wronskian

Notes:: See Miller (1955, p. 81).
Keywords:: parabolic cylinder functions
Permalink:: http://dlmf.nist.gov/12.14.ii

12.14.1 $\mathop{W\/}\nolimits\!\left(a,0\right)=2^{{-\frac{3}{4}}}\left|\frac{\mathop{% \Gamma\/}\nolimits\!\left(\tfrac{1}{4}+\tfrac{1}{2}ia\right)}{\mathop{\Gamma\/% }\nolimits\!\left(\tfrac{3}{4}+\tfrac{1}{2}ia\right)}\right|^{{\frac{1}{2}}},$

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, $\mathop{W\/}\nolimits\!\left(a,x\right)$ : parabolic cylinder function and : real or complex parameter
A&S Ref:: 19.17.4 (modification of)
Permalink:: http://dlmf.nist.gov/12.14.E1
Encodings:: TeX, pMML, png

12.14.2 ${\mathop{W\/}\nolimits^{{\prime}}}\!\left(a,0\right)=-2^{{-\frac{1}{4}}}\left|% \frac{\mathop{\Gamma\/}\nolimits\!\left(\tfrac{3}{4}+\tfrac{1}{2}ia\right)}{% \mathop{\Gamma\/}\nolimits\!\left(\tfrac{1}{4}+\tfrac{1}{2}ia\right)}\right|^{% {\frac{1}{2}}}.$

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, $\mathop{W\/}\nolimits\!\left(a,x\right)$ : parabolic cylinder function and : real or complex parameter
A&S Ref:: 19.17.5 (modification of)
Permalink:: http://dlmf.nist.gov/12.14.E2
Encodings:: TeX, pMML, png

12.14.3 $\mathop{\mathscr{W}\/}\nolimits\left\{\mathop{W\/}\nolimits\!\left(a,x\right),% \mathop{W\/}\nolimits\!\left(a,-x\right)\right\}=1.$

Symbols:: $\mathop{\mathscr{W}\/}\nolimits$ : Wronskian, $\mathop{W\/}\nolimits\!\left(a,x\right)$ : parabolic cylinder function, : real variable and : real or complex parameter
A&S Ref:: 19.18.1
Permalink:: http://dlmf.nist.gov/12.14.E3
Encodings:: TeX, pMML, png

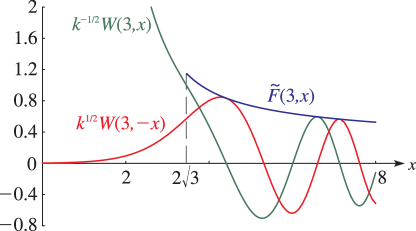
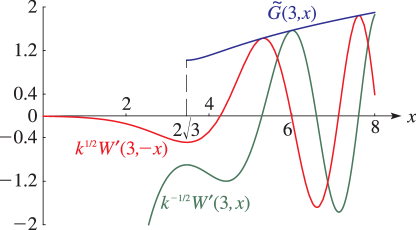
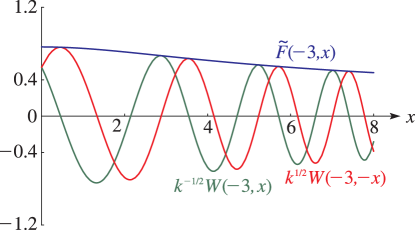
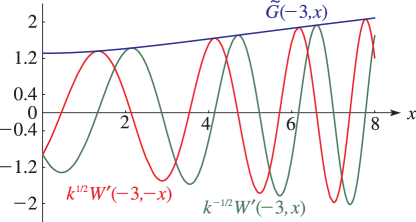
§12.14(iii) Graphs

Notes:: These graphs were produced at NIST.
Keywords:: parabolic cylinder functions
Referenced by:: §12.14(x)
Permalink:: http://dlmf.nist.gov/12.14.iii

For the modulus functions $\widetilde{F}(a,x)$ and $\widetilde{G}(a,x)$ see §12.14(x).

Figure 12.14.1: $k^{{-\ifrac{1}{2}}}\mathop{W\/}\nolimits\!\left(3,x\right)$ , $k^{{\ifrac{1}{2}}}\mathop{W\/}\nolimits\!\left(3,-x\right)$ , $\widetilde{F}(3,x)$ , $0\leq x\leq 8$ .

Symbols:: $\mathop{W\/}\nolimits\!\left(a,x\right)$ : parabolic cylinder function, : real variable and
Permalink:: http://dlmf.nist.gov/12.14.F1
Encodings:: pdf, png

Figure 12.14.2: $k^{{-\ifrac{1}{2}}}{\mathop{W\/}\nolimits^{{\prime}}}\!\left(3,x\right)$ , $k^{{\ifrac{1}{2}}}{\mathop{W\/}\nolimits^{{\prime}}}\!\left(3,-x\right)$ , $\widetilde{G}(3,x)$ , $0\leq x\leq 8$ .

Symbols:: $\mathop{W\/}\nolimits\!\left(a,x\right)$ : parabolic cylinder function, : real variable and
Permalink:: http://dlmf.nist.gov/12.14.F2
Encodings:: pdf, png

Figure 12.14.3: $k^{{-\ifrac{1}{2}}}\mathop{W\/}\nolimits\!\left(-3,x\right)$ , $k^{{\ifrac{1}{2}}}\mathop{W\/}\nolimits\!\left(-3,-x\right)$ , $\widetilde{F}(-3,x)$ , $0\leq x\leq 8$ .

Symbols:: $\mathop{W\/}\nolimits\!\left(a,x\right)$ : parabolic cylinder function, : real variable and
Permalink:: http://dlmf.nist.gov/12.14.F3
Encodings:: pdf, png

Figure 12.14.4: $k^{{-\ifrac{1}{2}}}{\mathop{W\/}\nolimits^{{\prime}}}\!\left(-3,x\right),k^{{% \ifrac{1}{2}}}{\mathop{W\/}\nolimits^{{\prime}}}\!\left(-3,-x\right)$ , $\widetilde{G}(-3,x)$ , $0\leq x\leq 8$ .

Symbols:: $\mathop{W\/}\nolimits\!\left(a,x\right)$ : parabolic cylinder function, : real variable and
Permalink:: http://dlmf.nist.gov/12.14.F4
Encodings:: pdf, png

§12.14(iv) Connection Formula

Notes:: See Miller (1955, p. 26).
Keywords:: parabolic cylinder functions
Permalink:: http://dlmf.nist.gov/12.14.iv

12.14.4 $\mathop{W\/}\nolimits\!\left(a,x\right)=\sqrt{k/2}\,e^{{\frac{1}{4}\pi a}}% \left(e^{{i\rho}}\mathop{U\/}\nolimits\!\left(ia,xe^{{-\pi i/4}}\right)+e^{{-i% \rho}}\mathop{U\/}\nolimits\!\left(-ia,xe^{{\pi i/4}}\right)\right),$

Symbols:: : base of exponential function, $\mathop{U\/}\nolimits\!\left(a,z\right)$ : parabolic cylinder function, $\mathop{W\/}\nolimits\!\left(a,x\right)$ : parabolic cylinder function, : real variable, : real or complex parameter, and $\rho$
Permalink:: http://dlmf.nist.gov/12.14.E4
Encodings:: TeX, pMML, png

where

12.14.5

$k=\sqrt{1+e^{{2\pi a}}}-e^{{\pi a}},$

$1/k=\sqrt{1+e^{{2\pi a}}}+e^{{\pi a}},$

Symbols:: : base of exponential function, : real or complex parameter and
A&S Ref:: 19.17.8
Referenced by:: §12.14(x)
Permalink:: http://dlmf.nist.gov/12.14.E5
Encodings:: TeX, TeX, pMML, pMML, png, png

12.14.6 $\rho=\tfrac{1}{8}\pi+\tfrac{1}{2}\phi_{2},$

Symbols:: $\rho$ and $\phi_{2}$
Permalink:: http://dlmf.nist.gov/12.14.E6
Encodings:: TeX, pMML, png

12.14.7 $\phi_{2}=\mathop{\mathrm{ph}\/}\nolimits\mathop{\Gamma\/}\nolimits\!\left(% \tfrac{1}{2}+ia\right),$

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, $\mathop{\mathrm{ph}\/}\nolimits$ : phase, : real or complex parameter and $\phi_{2}$
A&S Ref:: 19.17.10
Referenced by:: §12.14(viii)
Permalink:: http://dlmf.nist.gov/12.14.E7
Encodings:: TeX, pMML, png

the branch of $\mathop{\mathrm{ph}\/}\nolimits$ being zero when and defined by continuity elsewhere.

§12.14(v) Power-Series Expansions

Notes:: See Miller (1955, p. 80).
Keywords:: parabolic cylinder functions
Referenced by:: ¶ ‣ §12.14(vii)
Permalink:: http://dlmf.nist.gov/12.14.v

12.14.8 $\mathop{W\/}\nolimits\!\left(a,x\right)=\mathop{W\/}\nolimits\!\left(a,0\right% )w_{1}(a,x)+{\mathop{W\/}\nolimits^{{\prime}}}\!\left(a,0\right)w_{2}(a,x).$

Symbols:: $\mathop{W\/}\nolimits\!\left(a,x\right)$ : parabolic cylinder function, : real variable, : real or complex parameter, $w_{1}(a,x)$ : even solution and $w_{2}(a,x)$ : odd solution
A&S Ref:: 19.17.1 (modification of)
Permalink:: http://dlmf.nist.gov/12.14.E8
Encodings:: TeX, pMML, png

Here $w_{1}(a,x)$ and $w_{2}(a,x)$ are the even and odd solutions of (12.2.3):

12.14.9 $w_{1}(a,x)=\sum_{{n=0}}^{\infty}\alpha_{n}(a)\frac{x^{{2n}}}{(2n)!},$

Symbols:: : : factorial, : real variable, : nonnegative integer, : real or complex parameter, $w_{1}(a,x)$ : even solution and $\alpha_{n}(a)$ : recursion
A&S Ref:: 19.16.1 (modification of)
Permalink:: http://dlmf.nist.gov/12.14.E9
Encodings:: TeX, pMML, png

12.14.10 $w_{2}(a,x)=\sum_{{n=0}}^{\infty}\beta_{n}(a)\frac{x^{{2n+1}}}{(2n+1)!},$

Symbols:: : : factorial, : real variable, : nonnegative integer, : real or complex parameter, $w_{2}(a,x)$ : odd solution and $\beta_{n}(a)$ : recursion
A&S Ref:: 19.16.2 (modification of)
Permalink:: http://dlmf.nist.gov/12.14.E10
Encodings:: TeX, pMML, png

where $\alpha_{n}(a)$ and $\beta_{n}(a)$ satisfy the recursion relations

12.14.11

$\alpha_{{n+2}}=a\alpha_{{n+1}}-\tfrac{1}{2}(n+1)(2n+1)\alpha_{{n}},$

$\beta_{{n+2}}=a\beta_{{n+1}}-\tfrac{1}{2}(n+1)(2n+3)\beta_{{n}},$

Symbols:: : nonnegative integer, : real or complex parameter, $\alpha_{n}(a)$ : recursion and $\beta_{n}(a)$ : recursion
Permalink:: http://dlmf.nist.gov/12.14.E11
Encodings:: TeX, TeX, pMML, pMML, png, png

with

12.14.12

$\alpha_{0}(a)=1,$

$\alpha_{1}(a)=a,$

$\beta_{0}(a)=1,$

$\beta_{1}(a)=a.$

Symbols:: : real or complex parameter, $\alpha_{n}(a)$ : recursion and $\beta_{n}(a)$ : recursion
A&S Ref:: 19.16.3 (modification of)
Permalink:: http://dlmf.nist.gov/12.14.E12
Encodings:: TeX, TeX, TeX, TeX, pMML, pMML, pMML, pMML, png, png, png, png

Other expansions, involving $\mathop{\cos\/}\nolimits\!\left(\tfrac{1}{4}x^{2}\right)$ and $\mathop{\sin\/}\nolimits\!\left(\tfrac{1}{4}x^{2}\right)$ , can be obtained from (12.4.3) to (12.4.6) by replacing by and by $xe^{{\ifrac{\pi i}{4}}}$ ; see Miller (1955, p. 80), and also (12.14.15) and (12.14.16).

§12.14(vi) Integral Representations

Keywords:: parabolic cylinder functions
Permalink:: http://dlmf.nist.gov/12.14.vi

These follow from the contour integrals of §12.5(ii), which are valid for general complex values of the argument and parameter . See Miller (1955, p. 26).

§12.14(vii) Relations to Other Functions

Notes:: See Miller (1955, pp. 43, 89).
Permalink:: http://dlmf.nist.gov/12.14.vii

¶ Bessel Functions

Keywords:: Bessel functions, parabolic cylinder functions

For the notation see §10.2(ii). When

12.14.13 $\mathop{W\/}\nolimits\!\left(0,\pm x\right)=2^{{-\frac{5}{4}}}\sqrt{\pi x}% \left(\mathop{J_{{-\frac{1}{4}}}\/}\nolimits\!\left(\tfrac{1}{4}x^{2}\right)% \mp\mathop{J_{{\frac{1}{4}}}\/}\nolimits\!\left(\tfrac{1}{4}x^{2}\right)\right),$

Symbols:: $\mathop{J_{{\nu}}\/}\nolimits\!\left(z\right)$ : Bessel function of the first kind, $\mathop{W\/}\nolimits\!\left(a,x\right)$ : parabolic cylinder function and : real variable
A&S Ref:: 19.25.4 (corrected)
Referenced by:: §36.2(ii)
Permalink:: http://dlmf.nist.gov/12.14.E13
Encodings:: TeX, pMML, png

12.14.14 $\frac{d}{dx}\mathop{W\/}\nolimits\!\left(0,\pm x\right)=-2^{{-\frac{9}{4}}}x% \sqrt{\pi x}\left(\mathop{J_{{\frac{3}{4}}}\/}\nolimits\!\left(\tfrac{1}{4}x^{% 2}\right)\pm\mathop{J_{{-\frac{3}{4}}}\/}\nolimits\!\left(\tfrac{1}{4}x^{2}% \right)\right).$

Symbols:: $\mathop{J_{{\nu}}\/}\nolimits\!\left(z\right)$ : Bessel function of the first kind, $\frac{df}{dx}$ : derivative of with respect to , $\mathop{W\/}\nolimits\!\left(a,x\right)$ : parabolic cylinder function and : real variable
A&S Ref:: 19.25.5
Permalink:: http://dlmf.nist.gov/12.14.E14
Encodings:: TeX, pMML, png

¶ Confluent Hypergeometric Functions

Keywords:: confluent hypergeometric functions, parabolic cylinder functions

For the notation see §13.2(i).

The even and odd solutions of (12.2.3) (see §12.14(v)) are given by

12.14.15 $w_{1}(a,x)=e^{{-\frac{1}{4}ix^{2}}}\mathop{M\/}\nolimits\!\left(\tfrac{1}{4}-% \tfrac{1}{2}ia,\tfrac{1}{2},\tfrac{1}{2}ix^{2}\right)=e^{{\frac{1}{4}ix^{2}}}% \mathop{M\/}\nolimits\!\left(\tfrac{1}{4}+\tfrac{1}{2}ia,\tfrac{1}{2},-\tfrac{% 1}{2}ix^{2}\right),$

Symbols:: $\mathop{M\/}\nolimits\!\left(a,b,z\right)$ : Kummer confluent hypergeometric function, : base of exponential function, : real variable, : real or complex parameter and $w_{1}(a,x)$ : even solution
A&S Ref:: 19.25.1 (modification of)
Referenced by:: §12.14(v)
Permalink:: http://dlmf.nist.gov/12.14.E15
Encodings:: TeX, pMML, png

12.14.16 $w_{2}(a,x)=xe^{{-\frac{1}{4}ix^{2}}}\mathop{M\/}\nolimits\!\left(\tfrac{3}{4}-% \tfrac{1}{2}ia,\tfrac{3}{2},\tfrac{1}{2}ix^{2}\right)=xe^{{\frac{1}{4}ix^{2}}}% \mathop{M\/}\nolimits\!\left(\tfrac{3}{4}+\tfrac{1}{2}ia,\tfrac{3}{2},-\tfrac{% 1}{2}ix^{2}\right).$

Symbols:: $\mathop{M\/}\nolimits\!\left(a,b,z\right)$ : Kummer confluent hypergeometric function, : base of exponential function, : real variable, : real or complex parameter and $w_{2}(a,x)$ : odd solution
A&S Ref:: 19.25.1 (modification of)
Referenced by:: §12.14(v)
Permalink:: http://dlmf.nist.gov/12.14.E16
Encodings:: TeX, pMML, png

§12.14(viii) Asymptotic Expansions for Large Variable

Notes:: See Miller (1955, p. 82).
Keywords:: parabolic cylinder functions
Permalink:: http://dlmf.nist.gov/12.14.viii

Write

12.14.17 $\mathop{W\/}\nolimits\!\left(a,x\right)=\sqrt{\frac{2k}{x}}\left(s_{1}(a,x)% \mathop{\cos\/}\nolimits\omega-s_{2}(a,x)\mathop{\sin\/}\nolimits\omega\right),$

Symbols:: $\mathop{\cos\/}\nolimits z$ : cosine function, $\mathop{W\/}\nolimits\!\left(a,x\right)$ : parabolic cylinder function, $\mathop{\sin\/}\nolimits z$ : sine function, : real variable, : real or complex parameter, , $\omega$ and $s_{n}(a,x)$ : coefficients
A&S Ref:: 19.21.2 (modification of)
Permalink:: http://dlmf.nist.gov/12.14.E17
Encodings:: TeX, pMML, png

12.14.18 $\mathop{W\/}\nolimits\!\left(a,-x\right)=\sqrt{\frac{2}{kx}}\left(s_{1}(a,x)% \mathop{\sin\/}\nolimits\omega+s_{2}(a,x)\mathop{\cos\/}\nolimits\omega\right),$

Symbols:: $\mathop{\cos\/}\nolimits z$ : cosine function, $\mathop{W\/}\nolimits\!\left(a,x\right)$ : parabolic cylinder function, $\mathop{\sin\/}\nolimits z$ : sine function, : real variable, : real or complex parameter, , $\omega$ and $s_{n}(a,x)$ : coefficients
A&S Ref:: 19.21.3 (modification of)
Permalink:: http://dlmf.nist.gov/12.14.E18
Encodings:: TeX, pMML, png

where

12.14.19 $\omega=\tfrac{1}{4}x^{2}-a\mathop{\ln\/}\nolimits x+\tfrac{1}{4}\pi+\tfrac{1}{% 2}\phi_{2},$

Symbols:: $\mathop{\ln\/}\nolimits z$ : principal branch of logarithm function, : real variable, : real or complex parameter, $\phi_{2}$ and $\omega$
Permalink:: http://dlmf.nist.gov/12.14.E19
Encodings:: TeX, pMML, png

with $\phi_{2}$ given by (12.14.7). Then as $x\to\infty$

12.14.20 $s_{1}(a,x)\sim 1+\frac{d_{2}}{1!2x^{2}}-\frac{c_{4}}{2!2^{2}x^{4}}-\frac{d_{6}% }{3!2^{3}x^{6}}+\frac{c_{8}}{4!2^{4}x^{8}}+\cdots,$

Symbols:: : : factorial, $\sim$ : asymptotic equality, : real variable, : real or complex parameter, $c_{{2r}}$ : coefficients, $d_{{2r}}$ : coefficients and $s_{n}(a,x)$ : coefficients
A&S Ref:: 19.21.5
Permalink:: http://dlmf.nist.gov/12.14.E20
Encodings:: TeX, pMML, png

12.14.21 $s_{2}(a,x)\sim-\frac{c_{2}}{1!2x^{2}}-\frac{d_{4}}{2!2^{2}x^{4}}+\frac{c_{6}}{% 3!2^{3}x^{6}}+\frac{d_{8}}{4!2^{4}x^{8}}-\cdots.$

Symbols:: : : factorial, $\sim$ : asymptotic equality, : real variable, : real or complex parameter, $c_{{2r}}$ : coefficients, $d_{{2r}}$ : coefficients and $s_{n}(a,x)$ : coefficients
A&S Ref:: 19.21.6
Permalink:: http://dlmf.nist.gov/12.14.E21
Encodings:: TeX, pMML, png

The coefficients $c_{{2r}}$ and $d_{{2r}}$ are obtainable by equating real and imaginary parts in

12.14.22 $c_{{2r}}+id_{{2r}}=\frac{\mathop{\Gamma\/}\nolimits\!\left(2r+\tfrac{1}{2}+ia% \right)}{\mathop{\Gamma\/}\nolimits\!\left(\tfrac{1}{2}+ia\right)}.$

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, : real or complex parameter, $c_{{2r}}$ : coefficients and $d_{{2r}}$ : coefficients
A&S Ref:: 19.21.7 (modification of)
Permalink:: http://dlmf.nist.gov/12.14.E22
Encodings:: TeX, pMML, png

Equivalently,

12.14.23 $s_{1}(a,x)+is_{2}(a,x)\sim\sum_{{r=0}}^{\infty}(-i)^{r}\frac{\left(\tfrac{1}{2% }+ia\right)_{{2r}}}{2^{r}r!x^{{2r}}}.$

Symbols:: $\left(a\right)_{{n}}$ : Pochhammer’s symbol, : : factorial, $\sim$ : asymptotic equality, : real variable, : real or complex parameter and $s_{n}(a,x)$ : coefficients
A&S Ref:: 19.21.8 (modification of)
Permalink:: http://dlmf.nist.gov/12.14.E23
Encodings:: TeX, pMML, png

§12.14(ix) Uniform Asymptotic Expansions for Large Parameter

Notes:: See Olver (1959).
Keywords:: parabolic cylinder functions
Referenced by:: §12.14(x), §2.8(iii)
Permalink:: http://dlmf.nist.gov/12.14.ix

The differential equation

12.14.24 $\frac{{d}^{2}w}{{dt}^{2}}=\mu^{4}(1-t^{2})w$

Symbols:: $\frac{df}{dx}$ : derivative of with respect to
Permalink:: http://dlmf.nist.gov/12.14.E24
Encodings:: TeX, pMML, png

follows from (12.2.3), and has solutions $\mathop{W\/}\nolimits\!\left(\tfrac{1}{2}\mu^{2},\pm\mu t\sqrt{2}\right)$ . For real $\mu$ and oscillations occur outside the -interval . Airy-type uniform asymptotic expansions can be used to include either one of the turning points $\pm 1$ . In the following expansions, obtained from Olver (1959), $\mu$ is large and positive, and $\delta$ is again an arbitrary small positive constant.

¶ Positive , $2\sqrt{a}<x<\infty$

Keywords:: parabolic cylinder functions

12.14.25 $\mathop{W\/}\nolimits\!\left(\tfrac{1}{2}\mu^{2},\mu t\sqrt{2}\right)\sim\frac% {2^{{-\frac{1}{2}}}e^{{-\frac{1}{4}\pi\mu^{2}}}l(\mu)}{(t^{2}-1)^{{\frac{1}{4}% }}}\left(\mathop{\cos\/}\nolimits\sigma\sum_{{s=0}}^{\infty}(-1)^{s}\frac{{% \cal{A}}_{{2s}}(t)}{\mu^{{4s}}}-\mathop{\sin\/}\nolimits\sigma\sum_{{s=0}}^{% \infty}(-1)^{s}\frac{{\cal{A}}_{{2s+1}}(t)}{\mu^{{4s+2}}}\right),$

Symbols:: $\mathop{\cos\/}\nolimits z$ : cosine function, : base of exponential function, $\mathop{W\/}\nolimits\!\left(a,x\right)$ : parabolic cylinder function, $\sim$ : asymptotic equality, $\mathop{\sin\/}\nolimits z$ : sine function, : nonnegative integer, $\mathcal{A}_{s}(t)$ : coefficients, $\sigma$ and $l(\mu)$
Referenced by:: ¶ ‣ §12.14(ix)
Permalink:: http://dlmf.nist.gov/12.14.E25
Encodings:: TeX, pMML, png

12.14.26 $\mathop{W\/}\nolimits\!\left(\tfrac{1}{2}\mu^{2},-\mu t\sqrt{2}\right)\sim% \frac{2^{{\frac{1}{2}}}e^{{\frac{1}{4}\pi\mu^{2}}}l(\mu)}{(t^{2}-1)^{{\frac{1}% {4}}}}\left(\mathop{\sin\/}\nolimits\sigma\sum_{{s=0}}^{\infty}(-1)^{s}\frac{{% \cal{A}}_{{2s}}(t)}{\mu^{{4s}}}+\mathop{\cos\/}\nolimits\sigma\sum_{{s=0}}^{% \infty}(-1)^{s}\frac{{\cal{A}}_{{2s+1}}(t)}{\mu^{{4s+2}}}\right),$

Symbols:: $\mathop{\cos\/}\nolimits z$ : cosine function, : base of exponential function, $\mathop{W\/}\nolimits\!\left(a,x\right)$ : parabolic cylinder function, $\sim$ : asymptotic equality, $\mathop{\sin\/}\nolimits z$ : sine function, : nonnegative integer, $\mathcal{A}_{s}(t)$ : coefficients, $\sigma$ and $l(\mu)$
Referenced by:: ¶ ‣ §12.14(ix)
Permalink:: http://dlmf.nist.gov/12.14.E26
Encodings:: TeX, pMML, png

uniformly for $t\in[1+\delta,\infty)$ . Here ${\cal{A}}_{s}(t)$ is as in §12.10(ii), $\sigma$ is defined by

12.14.27 $\sigma=\mu^{2}\xi+\tfrac{1}{4}\pi,$

Symbols:: $\xi$ and $\sigma$
Permalink:: http://dlmf.nist.gov/12.14.E27
Encodings:: TeX, pMML, png

with $\xi$ given by (12.10.7), and

12.14.28 $l(\mu)=\sqrt{2}e^{{\frac{1}{8}\pi\mu^{2}}}e^{{i(\frac{1}{2}\phi_{2}-\frac{1}{8% }\pi)}}g(\mu e^{{-\frac{1}{4}\pi i}}),$

Symbols:: : base of exponential function, $g(\mu)$ : expansion, $l(\mu)$ and $\phi_{2}$
Permalink:: http://dlmf.nist.gov/12.14.E28
Encodings:: TeX, pMML, png

with $g(\mu)$ as in §12.10(ii). The function $l(\mu)$ has the asymptotic expansion

12.14.29 $l(\mu)\sim\frac{2^{{\frac{1}{4}}}}{\mu^{{\frac{1}{2}}}}\sum_{{s=0}}^{\infty}% \frac{l_{s}}{\mu^{{4s}}},$

Symbols:: $\sim$ : asymptotic equality, : nonnegative integer, $l(\mu)$ and $l_{s}$ : coefficient
Permalink:: http://dlmf.nist.gov/12.14.E29
Encodings:: TeX, pMML, png

with

12.14.30

$l_{0}=1,$

$l_{1}=-\tfrac{1}{1152},$

$l_{2}=-\tfrac{16123}{398\;13120}.$

Symbols:: : nonnegative integer and $l_{s}$ : coefficient
Permalink:: http://dlmf.nist.gov/12.14.E30
Encodings:: TeX, TeX, TeX, pMML, pMML, pMML, png, png, png

¶ Positive , $-2\sqrt{a}<x<2\sqrt{a}$

12.14.31 $\mathop{W\/}\nolimits\!\left(\tfrac{1}{2}\mu^{2},\mu t\sqrt{2}\right)\sim\frac% {l(\mu)e^{{\mu^{2}\eta}}}{2^{{\frac{1}{2}}}e^{{\frac{1}{4}\pi\mu^{2}}}(1-t^{2}% )^{{\frac{1}{4}}}}\*\sum_{{s=0}}^{\infty}(-1)^{s}\frac{\widetilde{\cal{A}}_{s}% (t)}{\mu^{{2s}}},$

Symbols:: : base of exponential function, $\mathop{W\/}\nolimits\!\left(a,x\right)$ : parabolic cylinder function, $\sim$ : asymptotic equality, : nonnegative integer, $\eta$ and $l(\mu)$
Referenced by:: ¶ ‣ §12.14(ix)
Permalink:: http://dlmf.nist.gov/12.14.E31
Encodings:: TeX, pMML, png

uniformly for $t\in[-1+\delta,1-\delta]$ , with $\eta$ given by (12.10.23) and ${\widetilde{\cal A}}_{s}(t)$ given by (12.10.24).

The expansions for the derivatives corresponding to (12.14.25), (12.14.26), and (12.14.31) may be obtained by formal term-by-term differentiation with respect to ; compare the analogous results in §§12.10(ii)–12.10(v).

¶ Airy-type Uniform Expansions

Keywords:: parabolic cylinder functions

12.14.32 $\mathop{W\/}\nolimits\!\left(\tfrac{1}{2}\mu^{2},\mu t\sqrt{2}\right)\sim\frac% {\pi^{{\frac{1}{2}}}\mu^{{\frac{1}{3}}}l(\mu)}{2^{{\frac{1}{2}}}e^{{\frac{1}{4% }\pi\mu^{2}}}}\phi(\zeta)\left(\mathop{\mathrm{Bi}\/}\nolimits\!\left(-\mu^{{% \frac{4}{3}}}\zeta\right)\sum_{{s=0}}^{\infty}(-1)^{s}\frac{A_{s}(\zeta)}{\mu^% {{4s}}}+\frac{{\mathop{\mathrm{Bi}\/}\nolimits^{{\prime}}}\!\left(-\mu^{{\frac% {4}{3}}}\zeta\right)}{\mu^{{\frac{8}{3}}}}\sum_{{s=0}}^{\infty}(-1)^{s}\frac{B% _{s}(\zeta)}{\mu^{{4s}}}\right),$

Symbols:: $\mathop{\mathrm{Bi}\/}\nolimits\!\left(z\right)$ : Airy function, : base of exponential function, $\mathop{W\/}\nolimits\!\left(a,x\right)$ : parabolic cylinder function, $\sim$ : asymptotic equality, : nonnegative integer, $\zeta$ : change of variable, $\phi(\zeta)$ : function, $A_{s}(\zeta)$ : coefficients, $B_{s}(\zeta)$ : coefficients and $l(\mu)$
Permalink:: http://dlmf.nist.gov/12.14.E32
Encodings:: TeX, pMML, png

12.14.33 $\mathop{W\/}\nolimits\!\left(\tfrac{1}{2}\mu^{2},-\mu t\sqrt{2}\right)\sim% \frac{\pi^{{\frac{1}{2}}}\mu^{{\frac{1}{3}}}l(\mu)}{2^{{-\frac{1}{2}}}e^{{-% \frac{1}{4}\pi\mu^{2}}}}\phi(\zeta)\left(\mathop{\mathrm{Ai}\/}\nolimits\!% \left(-\mu^{{\frac{4}{3}}}\zeta\right)\sum_{{s=0}}^{\infty}(-1)^{s}\frac{A_{s}% (\zeta)}{\mu^{{4s}}}+\frac{{\mathop{\mathrm{Ai}\/}\nolimits^{{\prime}}}\!\left% (-\mu^{{\frac{4}{3}}}\zeta\right)}{\mu^{{\frac{8}{3}}}}\sum_{{s=0}}^{\infty}(-% 1)^{s}\frac{B_{s}(\zeta)}{\mu^{{4s}}}\right),$

Symbols:: $\mathop{\mathrm{Ai}\/}\nolimits\!\left(z\right)$ : Airy function, : base of exponential function, $\mathop{W\/}\nolimits\!\left(a,x\right)$ : parabolic cylinder function, $\sim$ : asymptotic equality, : nonnegative integer, $\zeta$ : change of variable, $\phi(\zeta)$ : function, $A_{s}(\zeta)$ : coefficients, $B_{s}(\zeta)$ : coefficients and $l(\mu)$
Permalink:: http://dlmf.nist.gov/12.14.E33
Encodings:: TeX, pMML, png

uniformly for $t\in[-1+\delta,\infty)$ , with $\zeta$ , $\phi(\zeta)$ , $A_{s}(\zeta)$ , and $B_{s}(\zeta)$ as in §12.10(vii). For the corresponding expansions for the derivatives see Olver (1959).

¶ Negative , $-\infty<x<\infty$

Keywords:: parabolic cylinder functions

In this case there are no real turning points, and the solutions of (12.2.3), with replaced by , oscillate on the entire real -axis.

12.14.34 $\mathop{W\/}\nolimits\!\left(-\tfrac{1}{2}\mu^{2},\mu t\sqrt{2}\right)\sim% \frac{l(\mu)}{(t^{2}+1)^{{\frac{1}{4}}}}\left(\mathop{\cos\/}\nolimits% \overline{\sigma}\sum_{{s=0}}^{\infty}\frac{(-1)^{s}\overline{u}_{{2s}}(t)}{(t% ^{2}+1)^{{3s}}\mu^{{4s}}}-\mathop{\sin\/}\nolimits\overline{\sigma}\sum_{{s=0}% }^{\infty}\frac{(-1)^{s}\overline{u}_{{2s+1}}(t)}{(t^{2}+1)^{{3s+\frac{3}{2}}}% \mu^{{4s+2}}}\right),$

Symbols:: $\mathop{\cos\/}\nolimits z$ : cosine function, $\mathop{W\/}\nolimits\!\left(a,x\right)$ : parabolic cylinder function, $\sim$ : asymptotic equality, $\mathop{\sin\/}\nolimits z$ : sine function, : nonnegative integer, $\sigma$ and $l(\mu)$
Permalink:: http://dlmf.nist.gov/12.14.E34
Encodings:: TeX, pMML, png

12.14.35 ${\mathop{W\/}\nolimits^{{\prime}}}\!\left(-\tfrac{1}{2}\mu^{2},\mu t\sqrt{2}% \right)\sim-\frac{\mu}{\sqrt{2}}l(\mu)(t^{2}+1)^{{\frac{1}{4}}}\left(\mathop{% \sin\/}\nolimits\overline{\sigma}\sum_{{s=0}}^{\infty}\frac{(-1)^{s}\overline{% v}_{{2s}}(t)}{(t^{2}+1)^{{3s}}\mu^{{4s}}}+\mathop{\cos\/}\nolimits\overline{% \sigma}\sum_{{s=0}}^{\infty}\frac{(-1)^{s}\overline{v}_{{2s+1}}(t)}{(t^{2}+1)^% {{3s+\frac{3}{2}}}\mu^{{4s+2}}}\right),$

Symbols:: $\mathop{\cos\/}\nolimits z$ : cosine function, $\mathop{W\/}\nolimits\!\left(a,x\right)$ : parabolic cylinder function, $\sim$ : asymptotic equality, $\mathop{\sin\/}\nolimits z$ : sine function, : nonnegative integer, $\sigma$ and $l(\mu)$
Permalink:: http://dlmf.nist.gov/12.14.E35
Encodings:: TeX, pMML, png

uniformly for $t\in\Real$ , where

12.14.36 ${\overline{\sigma}}=\mu^{2}{\overline{\xi}}+\tfrac{1}{4}\pi,$

Symbols:: $\sigma$
Permalink:: http://dlmf.nist.gov/12.14.E36
Encodings:: TeX, pMML, png

and ${\overline{\xi}}$ and the coefficients $\overline{u}_{{s}}(t)$ and $\overline{v}_{{s}}(t)$ as in §12.10(v).

§12.14(x) Modulus and Phase Functions

Notes:: See Miller (1955, p. 87).
Keywords:: parabolic cylinder functions
Referenced by:: §12.14(iii)
Permalink:: http://dlmf.nist.gov/12.14.x

As noted in §12.14(ix), when is negative the solutions of (12.2.3), with replaced by , are oscillatory on the whole real line; also, when is positive there is a central interval $-2\sqrt{a}<x<2\sqrt{a}$ in which the solutions are exponential in character. In the oscillatory intervals we write

12.14.37 $k^{{-\ifrac{1}{2}}}\mathop{W\/}\nolimits\!\left(a,x\right)+ik^{{\ifrac{1}{2}}}% \mathop{W\/}\nolimits\!\left(a,-x\right)=\widetilde{F}(a,x)e^{{i\widetilde{% \theta}(a,x)}},$

Symbols:: : base of exponential function, $\mathop{W\/}\nolimits\!\left(a,x\right)$ : parabolic cylinder function, : real variable, : real or complex parameter and
Permalink:: http://dlmf.nist.gov/12.14.E37
Encodings:: TeX, pMML, png

12.14.38 $k^{{-\ifrac{1}{2}}}{\mathop{W\/}\nolimits^{{\prime}}}\!\left(a,x\right)+ik^{{% \ifrac{1}{2}}}{\mathop{W\/}\nolimits^{{\prime}}}\!\left(a,-x\right)=-% \widetilde{G}(a,x)e^{{i\widetilde{\psi}(a,x)}},$

Symbols:: : base of exponential function, $\mathop{W\/}\nolimits\!\left(a,x\right)$ : parabolic cylinder function, : real variable, : real or complex parameter and
Permalink:: http://dlmf.nist.gov/12.14.E38
Encodings:: TeX, pMML, png

where is defined in (12.14.5), and $\widetilde{F}(a,x)$ (0), $\widetilde{\theta}(a,x)$ , $\widetilde{G}(a,x)$ (0), and $\widetilde{\psi}(a,x)$ are real. $\widetilde{F}$ or $\widetilde{G}$ is the modulus and $\widetilde{\theta}$ or $\widetilde{\psi}$ is the corresponding phase. Compare §12.2(vi).

For properties of the modulus and phase functions, including differential equations and asymptotic expansions for large , see Miller (1955, pp. 87–88). For graphs of the modulus functions see §12.14(iii).

§12.14(xi) Zeros of $\mathop{W\/}\nolimits\!\left(a,x\right)$ , ${\mathop{W\/}\nolimits^{{\prime}}}\!\left(a,x\right)$

Keywords:: parabolic cylinder functions
Permalink:: http://dlmf.nist.gov/12.14.xi

For asymptotic expansions of the zeros of $\mathop{W\/}\nolimits\!\left(a,x\right)$ and ${\mathop{W\/}\nolimits^{{\prime}}}\!\left(a,x\right)$ , see Olver (1959).

© 2010–2013 NIST / Privacy Policy / Disclaimer / Feedback; Version 1.0.6; Release date 2013-05-06 Math-Image version (See MathML) . A Printed Companionis available. 12.13 Sums 12.15 Generalized Parabolic Cylinder Functions

§12.14 The Function

Contents