§36.5 Stokes Sets

Permalink:: http://dlmf.nist.gov/36.5

§36.5(i) Definitions
§36.5(ii) Cuspoids
§36.5(iii) Umbilics
§36.5(iv) Visualizations

§36.5(i) Definitions

Keywords:: Stokes sets
Referenced by:: §36.5(iv)
Permalink:: http://dlmf.nist.gov/36.5.i

Stokes sets are surfaces (codimension one) in $\mathbf{x}$ space, across which $\mathop{\Psi _{{K}}\/}\nolimits\!(\mathbf{x};k)$ or $\mathop{\Psi^{{(\mathrm{U})}}\/}\nolimits\!(\mathbf{x};k)$ acquires an exponentially-small asymptotic contribution (in $k$ ), associated with a complex critical point of $\mathop{\Phi _{{K}}\/}\nolimits$ or $\mathop{\Phi^{{(\mathrm{U})}}\/}\nolimits$ . The Stokes sets are defined by the exponential dominance condition:

36.5.1

$\realpart{\left(\mathop{\Phi _{{K}}\/}\nolimits\!\left(t_{j}(\mathbf{x});\mathbf{x}\right)-\mathop{\Phi _{{K}}\/}\nolimits\!\left(t_{\mu}(\mathbf{x});\mathbf{x}\right)\right)}=0,$

$\realpart{\left(\mathop{\Phi^{{(\mathrm{U})}}\/}\nolimits\!\left(s_{j}(\mathbf{x}),t_{j}(\mathbf{x});\mathbf{x}\right)-\mathop{\Phi^{{(\mathrm{U})}}\/}\nolimits\!\left(s_{\mu}(\mathbf{x}),t_{\mu}(\mathbf{x});\mathbf{x}\right)\right)}=0,$

Symbols:: $\mathop{\Phi _{{K}}\/}\nolimits\!\left(t;\mathbf{x}\right)$ : cuspoid catastrophe, $\realpart{}$ : real part, $s$ : variable, $K$ : codimension, $t_{j}(\mathbf{x})$ : solutions and $j$ : real critical point
Referenced by:: §36.5(ii)
Permalink:: http://dlmf.nist.gov/36.5.E1
Encodings:: TeX, TeX, pMML, pMML, png, png

where $j$ denotes a real critical point (36.4.1) or (36.4.2), and $\mu$ denotes a critical point with complex $t$ or $s,t$ , connected with $j$ by a steepest-descent path (that is, a path where $\realpart{\Phi}=\mathrm{constant}$ ) in complex $t$ or $(s,t)$ space.

In the following subsections, only Stokes sets involving at least one real saddle are included unless stated otherwise.

§36.5(ii) Cuspoids

Notes:: See Wright (1980), Berry and Howls (1990). The common strategy employed in deriving the formulas in this subsection involves using the critical-point condition (36.4.1) to reduce the order of the catastrophe polynomials in (36.2.1), then solving (36.5.1) for the imaginary part of the complex critical point in terms of the value of the real critical point, which is itself determined by (36.4.1) and then used to generate the Stokes sets parametrically.
Keywords:: Pearcey integral, Stokes sets, cuspoids, swallowtail canonical integral
Referenced by:: §36.5(iii)
Permalink:: http://dlmf.nist.gov/36.5.ii

¶ $K=1$ . Airy Function

The Stokes set consists of the rays $\mathop{\mathrm{ph}\/}\nolimits x=\pm 2\pi/3$ in the complex $x$ -plane.

¶ $K=2$ . Cusp

The Stokes set is itself a cusped curve, connected to the cusp of the bifurcation set:

36.5.2 $y^{3}=\tfrac{27}{4}\left(\sqrt{27}-5\right)x^{2}=1.32403x^{2}.$

Symbols:: $y$ : real parameter and $x$ : real parameter
Permalink:: http://dlmf.nist.gov/36.5.E2
Encodings:: TeX, pMML, png

¶ $K=3$ . Swallowtail

The Stokes set takes different forms for $z=0$ , $z<0$ , and $z>0$ .

For $z=0$ , the set consists of the two curves

36.5.3

$x=B_{{\pm}}|y|^{{4/3}},$

$B_{{\pm}}=10^{{-1/3}}\left(2x_{{\pm}}^{{4/3}}-\tfrac{1}{2}x_{{\pm}}^{{-2/3}}\right),$

Symbols:: $y$ : real parameter, $x_{i}$ : real parameter and $x$ : real parameter
Permalink:: http://dlmf.nist.gov/36.5.E3
Encodings:: TeX, TeX, pMML, pMML, png, png

where $x_{{\pm}}$ are the two smallest positive roots of the equation

36.5.4 $80x^{5}-40x^{4}-55x^{3}+5x^{2}+20x-1=0,$

Symbols:: $x$ : real parameter
Permalink:: http://dlmf.nist.gov/36.5.E4
Encodings:: TeX, pMML, png

and

36.5.5

$B_{{-}}=-1.69916,$

$B_{{+}}=0.33912.$

Permalink:: http://dlmf.nist.gov/36.5.E5
Encodings:: TeX, TeX, pMML, pMML, png, png

For $z\neq 0$ , the Stokes set is expressed in terms of scaled coordinates

36.5.6

$X=x/z^{2},$

$Y=y/|z|^{{3/2}},$

Symbols:: $y$ : real parameter, $z$ : real parameter, $x$ : real parameter, $X$ : scaled coordinate and $Y$ : scaled coordinate
Referenced by:: ¶ ‣ §36.5(ii)
Permalink:: http://dlmf.nist.gov/36.5.E6
Encodings:: TeX, TeX, pMML, pMML, png, png

36.5.7 $X=\dfrac{9}{20}+20u^{4}-\frac{Y^{2}}{20u^{2}}+6u^{2}\mathop{\mathrm{sign}\/}\nolimits\!\left(z\right),$

Symbols:: $\mathop{\mathrm{sign}\/}\nolimits x$ : sign of $x$ , $z$ : real parameter, $X$ : scaled coordinate and $Y$ : scaled coordinate
Permalink:: http://dlmf.nist.gov/36.5.E7
Encodings:: TeX, pMML, png

where $u$ satisfies the equation

36.5.8 $16u^{5}-\frac{Y^{2}}{10u}+4u^{3}\mathop{\mathrm{sign}\/}\nolimits\!\left(z\right)-\frac{3}{10}|Y|\mathop{\mathrm{sign}\/}\nolimits\!\left(z\right)+4t^{5}+2t^{3}\mathop{\mathrm{sign}\/}\nolimits\!\left(z\right)+|Y|t^{2}=0,$

Symbols:: $\mathop{\mathrm{sign}\/}\nolimits x$ : sign of $x$ , $z$ : real parameter, $t$ : variable and $Y$ : scaled coordinate
Permalink:: http://dlmf.nist.gov/36.5.E8
Encodings:: TeX, pMML, png

in which

36.5.9 $t=-u+\left(\dfrac{|Y|}{10u}-u^{2}-\dfrac{3}{10}\mathop{\mathrm{sign}\/}\nolimits\!\left(z\right)\right)^{{1/2}}.$

Symbols:: $\mathop{\mathrm{sign}\/}\nolimits x$ : sign of $x$ , $z$ : real parameter, $t$ : variable and $Y$ : scaled coordinate
Referenced by:: ¶ ‣ §36.5(ii)
Permalink:: http://dlmf.nist.gov/36.5.E9
Encodings:: TeX, pMML, png

For $z<0$ , there are two solutions $u$ , provided that $|Y|>(\frac{2}{5})^{{1/2}}$ . They generate a pair of cusp-edged sheets connected to the cusped sheets of the swallowtail bifurcation set (§36.4).

For $z>0$ the Stokes set has two sheets. The first sheet corresponds to $x<0$ and is generated as a solution of Equations (36.5.6)–(36.5.9). The second sheet corresponds to $x>0$ and it intersects the bifurcation set (§36.4) smoothly along the line generated by $X=X_{1}=6.95643$ , $\left|Y\right|=\left|Y_{1}\right|=6.81337$ . For $\left|Y\right|>Y_{1}$ the second sheet is generated by a second solution of (36.5.6)–(36.5.9), and for $\left|Y\right|<Y_{1}$ it is generated by the roots of the polynomial equation

36.5.10 $160u^{6}+40u^{4}=Y^{2}.$

Symbols:: $Y$ : scaled coordinate
Permalink:: http://dlmf.nist.gov/36.5.E10
Encodings:: TeX, pMML, png

§36.5(iii) Umbilics

Notes:: See Berry and Howls (1990). The strategy used to derive the formulas in this subsection is the same as in §36.5(ii), but using the exponents in the representations (36.2.6) and (36.2.8).
Keywords:: Stokes sets, elliptic umbilic canonical integral, hyperbolic umbilic canonical integral, umbilics
Permalink:: http://dlmf.nist.gov/36.5.iii

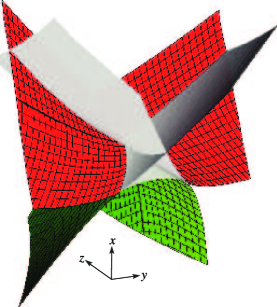
¶ Elliptic Umbilic Stokes Set (Codimension three)

This consists of three separate cusp-edged sheets connected to the cusp-edged sheets of the bifurcation set, and related by rotation about the $z$ -axis by $2\pi/3$ . One of the sheets is symmetrical under reflection in the plane $y=0$ , and is given by

36.5.11 $\frac{x}{z^{2}}=-1-12u^{2}+8u-\left|\frac{y}{z^{2}}\right|\dfrac{\frac{1}{3}-u}{\left(u\left(\frac{2}{3}-u\right)\right)^{{1/2}}}.$

Symbols:: $y$ : real parameter, $z$ : real parameter and $x$ : real parameter
Referenced by:: §36.5(iv)
Permalink:: http://dlmf.nist.gov/36.5.E11
Encodings:: TeX, pMML, png

Here $u$ is the root of the equation

36.5.12 $8u^{3}-4u^{2}-\left|\frac{y}{3z^{2}}\right|\left(\frac{u}{\tfrac{2}{3}-u}\right)^{{1/2}}=\frac{y^{2}}{6wz^{4}}-2w^{3}-2w^{2},$

Symbols:: $y$ : real parameter, $z$ : real parameter and $w$ : quantity
Permalink:: http://dlmf.nist.gov/36.5.E12
Encodings:: TeX, pMML, png

with

36.5.13 $w=u-\tfrac{2}{3}+\left(\left(\tfrac{2}{3}-u\right)^{2}+\left|\frac{y}{6z^{2}}\right|\left(\frac{\frac{2}{3}-u}{u}\right)^{{1/2}}\right)^{{1/2}},$

Symbols:: $y$ : real parameter, $z$ : real parameter and $w$ : quantity
Permalink:: http://dlmf.nist.gov/36.5.E13
Encodings:: TeX, pMML, png

and such that

36.5.14 $0<u<\tfrac{1}{6}.$

Permalink:: http://dlmf.nist.gov/36.5.E14
Encodings:: TeX, pMML, png

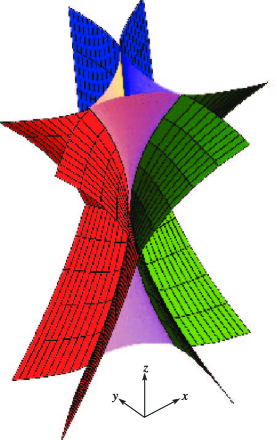
¶ Hyperbolic Umbilic Stokes Set (Codimension three)

This consists of a cusp-edged sheet connected to the cusp-edged sheet of the bifurcation set and intersecting the smooth sheet of the bifurcation set. With coordinates

36.5.15

$X=(x-y)/z^{2},$

$Y=\tfrac{1}{2}+\left((x+y)/z^{2}\right),$

Symbols:: $y$ : real parameter, $z$ : real parameter, $x$ : real parameter and $X$ : scaled coordinate
Permalink:: http://dlmf.nist.gov/36.5.E15
Encodings:: TeX, TeX, pMML, pMML, png, png

the intersection lines with the bifurcation set are generated by $|X|=X_{2}=0.45148$ , $Y=Y_{2}=0.59693$ . Define

36.5.16

$Y(u,X)=8u-24u^{2}+X\dfrac{u-\tfrac{1}{6}}{\left(u\left(u-\tfrac{1}{3}\right)\right)^{{1/2}}},$

$f(u,X)=16u^{3}-4u^{2}-\tfrac{1}{6}|X|\left(\dfrac{u}{u-\tfrac{1}{3}}\right)^{{1/2}}.$

Symbols:: $X$ : scaled coordinate
Permalink:: http://dlmf.nist.gov/36.5.E16
Encodings:: TeX, TeX, pMML, pMML, png, png

When $|X|>X_{2}$ the Stokes set $Y_{{\mathrm{S}}}(X)$ is given by

36.5.17 $Y_{{\mathrm{S}}}(X)=Y(u,|X|),$

Symbols:: $X$ : scaled coordinate
Permalink:: http://dlmf.nist.gov/36.5.E17
Encodings:: TeX, pMML, png

where $u$ is the root of the equation

36.5.18 $f(u,X)=f(-u+\tfrac{1}{3},X),$

Symbols:: $X$ : scaled coordinate
Permalink:: http://dlmf.nist.gov/36.5.E18
Encodings:: TeX, pMML, png

such that $u>\tfrac{1}{3}$ . This part of the Stokes set connects two complex saddles.

Alternatively, when $|X|<X_{2}$

36.5.19 $Y_{{\mathrm{S}}}(X)=Y(-u,-|X|),$

Symbols:: $X$ : scaled coordinate
Permalink:: http://dlmf.nist.gov/36.5.E19
Encodings:: TeX, pMML, png

where $u$ is the positive root of the equation

36.5.20 $f(-u,X)=\dfrac{X^{2}}{12w}+4w^{3}-2w^{2},$

Symbols:: $w$ : quantity and $X$ : scaled coordinate
Permalink:: http://dlmf.nist.gov/36.5.E20
Encodings:: TeX, pMML, png

in which

36.5.21 $w=(\tfrac{1}{3}+u)\left(1-\left(1-\dfrac{|X|}{12u^{{1/2}}(\tfrac{1}{3}+u)^{{3/2}}}\right)^{{1/2}}\right).$

Symbols:: $w$ : quantity and $X$ : scaled coordinate
Referenced by:: §36.5(iv)
Permalink:: http://dlmf.nist.gov/36.5.E21
Encodings:: TeX, pMML, png

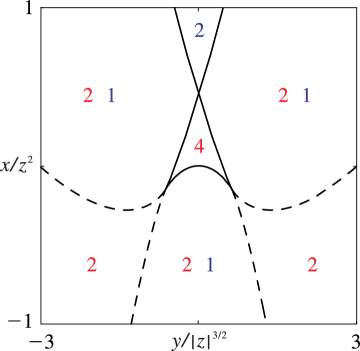
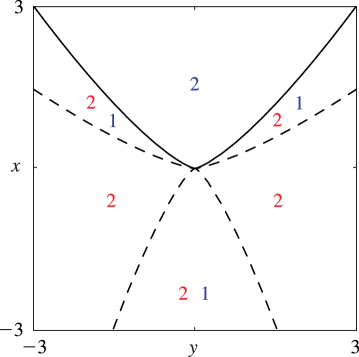
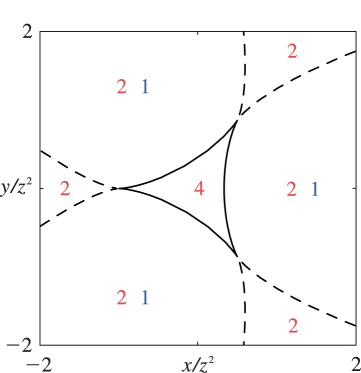
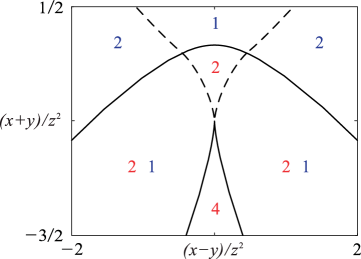
§36.5(iv) Visualizations

Notes:: The graphics were generated by the authors. For Figures 36.5.2–36.5.9, Eqs. (36.5.11)–(36.5.21) were used in parametric form $x=x(y)$ , and checked against the numerical computations in Berry and Howls (1990) (which were based directly on the definitions given in §36.5(i)).
Keywords:: Pearcey integral, Stokes sets, hyperbolic umbilic catastrophe, swallowtail canonical integral
Permalink:: http://dlmf.nist.gov/36.5.iv

In Figures 36.5.1–36.5.6 the plane is divided into regions by the dashed curves (Stokes sets) and the continuous curves (bifurcation sets). Red and blue numbers in each region correspond, respectively, to the numbers of real and complex critical points that contribute to the asymptotics of the canonical integral away from the bifurcation sets. In Figure 36.5.4 the part of the Stokes surface inside the bifurcation set connects two complex saddles. The distribution of real and complex critical points in Figures 36.5.5 and 36.5.6 follows from consistency with Figure 36.5.1 and the fact that there are four real saddles in the inner regions.