§28.5 Second Solutions $\mathop{\mathrm{fe}_{{n}}\/}\nolimits$ , $\mathop{\mathrm{ge}_{{n}}\/}\nolimits$

Permalink:: http://dlmf.nist.gov/28.5

§28.5(i) Definitions
§28.5(ii) Graphics: Line Graphs of Second Solutions of Mathieu’s Equation

§28.5(i) Definitions

Notes:: See McLachlan (1947, pp. 141–155) and Meixner and Schäfke (1954, §2.72). For a proof of the Theorem of Ince see Arscott (1964b, §2.4).
Keywords:: Mathieu’s equation, Theorem of Ince
Referenced by:: §28.2(iv), §28.22(i), §28.28(i)
Permalink:: http://dlmf.nist.gov/28.5.i

¶ Theorem of Ince (1922)

Keywords:: Mathieu’s equation

If a nontrivial solution of Mathieu’s equation with $q\neq 0$ has period $\pi$ or $2\pi$ , then any linearly independent solution cannot have either period.

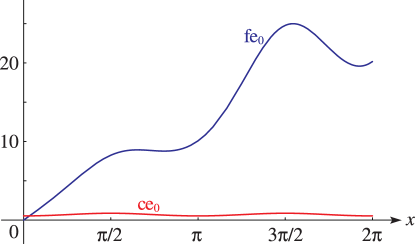
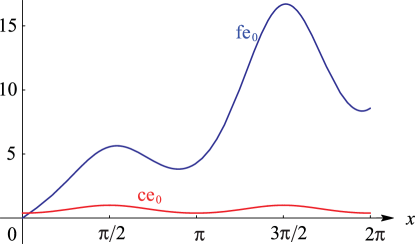
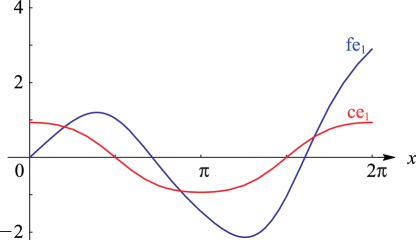
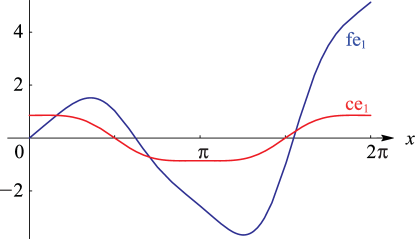
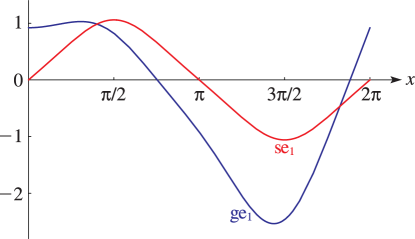
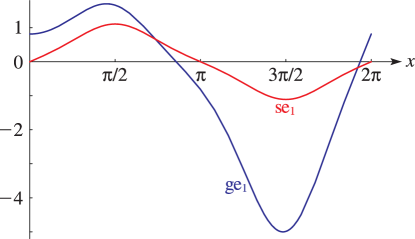
Second solutions of (28.2.1) are given by

28.5.1 $\mathop{\mathrm{fe}_{{n}}\/}\nolimits\!\left(z,q\right)=C_{n}(q)\left(z\mathop{\mathrm{ce}_{{n}}\/}\nolimits\!\left(z,q\right)+f_{n}(z,q)\right),$

Defines:: $\mathop{\mathrm{fe}_{{n}}\/}\nolimits\!\left(z,q\right)$ : second solution, Mathieu’s equation
Symbols:: $\mathop{\mathrm{ce}_{{n}}\/}\nolimits\!\left(z,q\right)$ : Mathieu function, $q=h^{2}$ : parameter, $n$ : integer, $z$ : complex variable, $f_{n}(z,q)$ : functions and $C_{n}(q)$ : factor
A&S Ref:: 20.3.6 (in different form)
Referenced by:: ¶ ‣ §28.5(i), ¶ ‣ §28.5(i)
Permalink:: http://dlmf.nist.gov/28.5.E1
Encodings:: TeX, pMML, png

when $a=\mathop{a_{{n}}\/}\nolimits\!\left(q\right)$ , $n=0,1,2,\dots$ , and by

28.5.2 $\mathop{\mathrm{ge}_{{n}}\/}\nolimits\!\left(z,q\right)=S_{n}(q)\left(z\mathop{\mathrm{se}_{{n}}\/}\nolimits\!\left(z,q\right)+g_{n}(z,q)\right),$

Defines:: $\mathop{\mathrm{ge}_{{n}}\/}\nolimits\!\left(z,q\right)$ : second solution, Mathieu’s equation
Symbols:: $\mathop{\mathrm{se}_{{n}}\/}\nolimits\!\left(z,q\right)$ : Mathieu function, $q=h^{2}$ : parameter, $n$ : integer, $z$ : complex variable, $g_{n}(z,q)$ : functions and $S_{n}(q)$ : factor
A&S Ref:: 20.3.7 (in different form)
Referenced by:: ¶ ‣ §28.5(i), ¶ ‣ §28.5(i)
Permalink:: http://dlmf.nist.gov/28.5.E2
Encodings:: TeX, pMML, png

when $a=\mathop{b_{{n}}\/}\nolimits\!\left(q\right)$ , $n=1,2,3,\dots$ . For $m=0,1,2,\dots$ , we have

28.5.3 $\begin{array}[]{ll}f_{{2m}}(z,q)&\mbox{$\pi$-periodic, odd},\\ f_{{2m+1}}(z,q)&\mbox{$\pi$-antiperiodic, odd},\end{array}$

Symbols:: $m$ : integer, $q=h^{2}$ : parameter, $n$ : integer, $z$ : complex variable and $f_{n}(z,q)$ : functions
Permalink:: http://dlmf.nist.gov/28.5.E3
Encodings:: TeX, pMML, png

and

28.5.4 $\begin{array}[]{ll}g_{{2m+1}}(z,q)&\mbox{$\pi$-antiperiodic, even},\\ g_{{2m+2}}(z,q)&\mbox{$\pi$-periodic, even};\end{array}$

Symbols:: $m$ : integer, $q=h^{2}$ : parameter, $n$ : integer, $z$ : complex variable and $g_{n}(z,q)$ : functions
Permalink:: http://dlmf.nist.gov/28.5.E4
Encodings:: TeX, pMML, png

compare §28.2(vi). The functions $f_{n}(z,q)$ , $g_{n}(z,q)$ are unique.

The factors $C_{n}(q)$ and $S_{n}(q)$ in (28.5.1) and (28.5.2) are normalized so that

28.5.5 $(C_{n}(q))^{2}\int _{0}^{{2\pi}}(f_{n}(x,q))^{2}dx=(S_{n}(q))^{2}\int _{0}^{{2\pi}}(g_{n}(x,q))^{2}dx=\pi.$

Symbols:: $dx$ : differential of $x$ , $\int$ : integral, $q=h^{2}$ : parameter, $n$ : integer, $x$ : real variable, $f_{n}(z,q)$ : functions, $g_{n}(z,q)$ : functions, $C_{n}(q)$ : factor and $S_{n}(q)$ : factor
Permalink:: http://dlmf.nist.gov/28.5.E5
Encodings:: TeX, pMML, png

As $q\to 0$ with $n\neq 0$ , $C_{n}(q)\to 0$ , $S_{n}(q)\to 0$ , $C_{n}(q)f_{n}(z,q)\to\mathop{\sin\/}\nolimits nz$ , and $S_{n}(q)g_{n}(z,q)\to\mathop{\cos\/}\nolimits nz$ . This determines the signs of $C_{n}(q)$ and $S_{n}(q)$ . (Other normalizations for $C_{n}(q)$ and $S_{n}(q)$ can be found in the literature, but most formulas—including connection formulas—are unaffected since $\mathop{\mathrm{fe}_{{n}}\/}\nolimits\!\left(z,q\right)/C_{n}(q)$ and $\mathop{\mathrm{ge}_{{n}}\/}\nolimits\!\left(z,q\right)/S_{n}(q)$ are invariant.)

28.5.6

$C_{{2m}}(-q)=C_{{2m}}(q),$

$C_{{2m+1}}(-q)=S_{{2m+1}}(q),$

$S_{{2m+2}}(-q)=S_{{2m+2}}(q).$

Symbols:: $m$ : integer, $q=h^{2}$ : parameter, $C_{n}(q)$ : factor and $S_{n}(q)$ : factor
Permalink:: http://dlmf.nist.gov/28.5.E6
Encodings:: TeX, TeX, TeX, pMML, pMML, pMML, png, png, png

For $q=0$ ,

28.5.7

$\mathop{\mathrm{fe}_{{0}}\/}\nolimits\!\left(z,0\right)=z,$

$\mathop{\mathrm{fe}_{{n}}\/}\nolimits\!\left(z,0\right)=\mathop{\sin\/}\nolimits nz,$

$\mathop{\mathrm{ge}_{{n}}\/}\nolimits\!\left(z,0\right)=\mathop{\cos\/}\nolimits nz$ , $n=1,2,3,\dots$ ;

Symbols:: $\mathop{\mathrm{fe}_{{n}}\/}\nolimits\!\left(z,q\right)$ : second solution, Mathieu’s equation, $\mathop{\mathrm{ge}_{{n}}\/}\nolimits\!\left(z,q\right)$ : second solution, Mathieu’s equation, $\mathop{\cos\/}\nolimits z$ : cosine function, $\mathop{\sin\/}\nolimits z$ : sine function, $n$ : integer and $z$ : complex variable
Permalink:: http://dlmf.nist.gov/28.5.E7
Encodings:: TeX, TeX, TeX, pMML, pMML, pMML, png, png, png

compare (28.2.29).

As a consequence of the factor $z$ on the right-hand sides of (28.5.1), (28.5.2), all solutions of Mathieu’s equation that are linearly independent of the periodic solutions are unbounded as $z\to\pm\infty$ on $\Real$ .

¶ Wronskians

Keywords:: Fourier series, Mathieu functions, Mathieu’s equation

28.5.8 $\mathop{\mathscr{W}\/}\nolimits\left\{\mathop{\mathrm{ce}_{{n}}\/}\nolimits,\mathop{\mathrm{fe}_{{n}}\/}\nolimits\right\}=\mathop{\mathrm{ce}_{{n}}\/}\nolimits\!\left(0,q\right){\mathop{\mathrm{fe}_{{n}}\/}\nolimits^{{\prime}}}\!\left(0,q\right),$

Symbols:: $\mathop{\mathrm{ce}_{{n}}\/}\nolimits\!\left(z,q\right)$ : Mathieu function, $\mathop{\mathrm{fe}_{{n}}\/}\nolimits\!\left(z,q\right)$ : second solution, Mathieu’s equation, $\mathop{\mathscr{W}\/}\nolimits$ : Wronskian, $q=h^{2}$ : parameter and $n$ : integer
Permalink:: http://dlmf.nist.gov/28.5.E8
Encodings:: TeX, pMML, png

28.5.9 $\mathop{\mathscr{W}\/}\nolimits\left\{\mathop{\mathrm{se}_{{n}}\/}\nolimits,\mathop{\mathrm{ge}_{{n}}\/}\nolimits\right\}=-{\mathop{\mathrm{se}_{{n}}\/}\nolimits^{{\prime}}}\!\left(0,q\right)\mathop{\mathrm{ge}_{{n}}\/}\nolimits\!\left(0,q\right).$

Symbols:: $\mathop{\mathrm{ge}_{{n}}\/}\nolimits\!\left(z,q\right)$ : second solution, Mathieu’s equation, $\mathop{\mathrm{se}_{{n}}\/}\nolimits\!\left(z,q\right)$ : Mathieu function, $\mathop{\mathscr{W}\/}\nolimits$ : Wronskian, $q=h^{2}$ : parameter and $n$ : integer
Permalink:: http://dlmf.nist.gov/28.5.E9
Encodings:: TeX, pMML, png

See (28.22.12) for ${\mathop{\mathrm{fe}_{{n}}\/}\nolimits^{{\prime}}}\!\left(0,q\right)$ and $\mathop{\mathrm{ge}_{{n}}\/}\nolimits\!\left(0,q\right)$ .

For further information on $C_{n}(q)$ , $S_{n}(q)$ , and expansions of $f_{n}(z,q)$ , $g_{n}(z,q)$ in Fourier series or in series of $\mathop{\mathrm{ce}_{{n}}\/}\nolimits$ , $\mathop{\mathrm{se}_{{n}}\/}\nolimits$ functions, see McLachlan (1947, Chapter VII) or Meixner and Schäfke (1954, §2.72).

§28.5(ii) Graphics: Line Graphs of Second Solutions of Mathieu’s Equation

Notes:: Figures 28.5.1–28.5.6 were produced at NIST.
Keywords:: Mathieu’s equation
Permalink:: http://dlmf.nist.gov/28.5.ii

¶ Odd Second Solutions

Figure 28.5.1: $\mathop{\mathrm{fe}_{{0}}\/}\nolimits\!\left(x,0.5\right)$ for $0\leq x\leq 2\pi$ and (for comparison) $\mathop{\mathrm{ce}_{{0}}\/}\nolimits\!\left(x,0.5\right)$ .

Symbols:: $\mathop{\mathrm{ce}_{{n}}\/}\nolimits\!\left(z,q\right)$ : Mathieu function, $\mathop{\mathrm{fe}_{{n}}\/}\nolimits\!\left(z,q\right)$ : second solution, Mathieu’s equation and $x$ : real variable
Referenced by:: §28.5(ii)
Permalink:: http://dlmf.nist.gov/28.5.F1
Encodings:: pdf, png

Figure 28.5.2: $\mathop{\mathrm{fe}_{{0}}\/}\nolimits\!\left(x,1\right)$ for $0\leq x\leq 2\pi$ and (for comparison) $\mathop{\mathrm{ce}_{{0}}\/}\nolimits\!\left(x,1\right)$ .

Symbols:: $\mathop{\mathrm{ce}_{{n}}\/}\nolimits\!\left(z,q\right)$ : Mathieu function, $\mathop{\mathrm{fe}_{{n}}\/}\nolimits\!\left(z,q\right)$ : second solution, Mathieu’s equation and $x$ : real variable
Permalink:: http://dlmf.nist.gov/28.5.F2
Encodings:: pdf, png

Figure 28.5.3: $\mathop{\mathrm{fe}_{{1}}\/}\nolimits\!\left(x,0.5\right)$ for $0\leq x\leq 2\pi$ and (for comparison) $\mathop{\mathrm{ce}_{{1}}\/}\nolimits\!\left(x,0.5\right)$ .

Symbols:: $\mathop{\mathrm{ce}_{{n}}\/}\nolimits\!\left(z,q\right)$ : Mathieu function, $\mathop{\mathrm{fe}_{{n}}\/}\nolimits\!\left(z,q\right)$ : second solution, Mathieu’s equation and $x$ : real variable
Permalink:: http://dlmf.nist.gov/28.5.F3
Encodings:: pdf, png

Figure 28.5.4: $\mathop{\mathrm{fe}_{{1}}\/}\nolimits\!\left(x,1\right)$ for $0\leq x\leq 2\pi$ and (for comparison) $\mathop{\mathrm{ce}_{{1}}\/}\nolimits\!\left(x,1\right)$ .

Symbols:: $\mathop{\mathrm{ce}_{{n}}\/}\nolimits\!\left(z,q\right)$ : Mathieu function, $\mathop{\mathrm{fe}_{{n}}\/}\nolimits\!\left(z,q\right)$ : second solution, Mathieu’s equation and $x$ : real variable
Permalink:: http://dlmf.nist.gov/28.5.F4
Encodings:: pdf, png

¶ Even Second Solutions

Figure 28.5.5: $\mathop{\mathrm{ge}_{{1}}\/}\nolimits\!\left(x,0.5\right)$ for $0\leq x\leq 2\pi$ and (for comparison) $\mathop{\mathrm{se}_{{1}}\/}\nolimits\!\left(x,0.5\right)$ .

Symbols:: $\mathop{\mathrm{ge}_{{n}}\/}\nolimits\!\left(z,q\right)$ : second solution, Mathieu’s equation, $\mathop{\mathrm{se}_{{n}}\/}\nolimits\!\left(z,q\right)$ : Mathieu function and $x$ : real variable
Permalink:: http://dlmf.nist.gov/28.5.F5
Encodings:: pdf, png

Figure 28.5.6: $\mathop{\mathrm{ge}_{{1}}\/}\nolimits\!\left(x,1\right)$ for $0\leq x\leq 2\pi$ and (for comparison) $\mathop{\mathrm{se}_{{1}}\/}\nolimits\!\left(x,1\right)$ .

Symbols:: $\mathop{\mathrm{ge}_{{n}}\/}\nolimits\!\left(z,q\right)$ : second solution, Mathieu’s equation, $\mathop{\mathrm{se}_{{n}}\/}\nolimits\!\left(z,q\right)$ : Mathieu function and $x$ : real variable
Referenced by:: §28.5(ii)
Permalink:: http://dlmf.nist.gov/28.5.F6
Encodings:: pdf, png

§28.5 Second Solutions ,

Contents