§21.9 Integrable Equations

Notes:: See Dubrovin (1981) and Belokolos et al. (1994).
Keywords:: KP equation, Kadomtsev–Petviashvili equation, Korteweg–de Vries equation, Novikov’s conjecture, Riemann surface, Riemann theta functions, Schottky problem, Schrödinger equation, fluid dynamics, integrable differential equations, integrable equations, magnetic monopoles, string theory, water waves
Permalink:: http://dlmf.nist.gov/21.9

Riemann theta functions arise in the study of integrable differential equations that have applications in many areas, including fluid mechanics (Ablowitz and Segur (1981, Chapter 4)), magnetic monopoles (Ercolani and Sinha (1989)), and string theory (Deligne et al. (1999, Part 3)). Typical examples of such equations are the Korteweg–de Vries equation

21.9.1 $4u_{t}=6uu_{x}+u_{{xxx}},$

Symbols:: $u(x,y,t)$ : elevation
Permalink:: http://dlmf.nist.gov/21.9.E1
Encodings:: TeX, pMML, png

and the nonlinear Schrödinger equations

21.9.2 $iu_{t}=-\tfrac{1}{2}u_{{xx}}\pm|u|^{2}u.$

Symbols:: $u(x,y,t)$ : elevation
Permalink:: http://dlmf.nist.gov/21.9.E2
Encodings:: TeX, pMML, png

Here, and in what follows, $x,y$ , and $t$ suffixes indicate partial derivatives.

Particularly important for the use of Riemann theta functions is the Kadomtsev–Petviashvili (KP) equation, which describes the propagation of two-dimensional, long-wave length surface waves in shallow water (Ablowitz and Segur (1981, Chapter 4)):

21.9.3 $(-4u_{t}+6uu_{x}+u_{{xxx}})_{x}+3u_{{yy}}=0.$

Symbols:: $u(x,y,t)$ : elevation
Referenced by:: Figure 21.9.2, Figure 21.9.2, §21.9, Sidebar 21.SB2, Sidebar 21.SB2
Permalink:: http://dlmf.nist.gov/21.9.E3
Encodings:: TeX, pMML, png

Here $x$ and $y$ are spatial variables, $t$ is time, and $u(x,y,t)$ is the elevation of the surface wave. All quantities are made dimensionless by a suitable scaling transformation. The KP equation has a class of quasi-periodic solutions described by Riemann theta functions, given by

21.9.4 $u(x,y,t)=c+2\frac{{\partial}^{2}}{{\partial x}^{2}}\mathop{\ln\/}\nolimits\!\left(\mathop{\theta\/}\nolimits\!\left(\mathbf{k}x+\mathbf{l}y+\boldsymbol{{\omega}}t+\boldsymbol{{\phi}}\middle|\boldsymbol{{\Omega}}\right)\right),$

Symbols:: $\mathop{\theta\/}\nolimits\!\left(\mathbf{z}\middle|\boldsymbol{{\Omega}}\right)$ : Riemann theta function, $\mathop{\ln\/}\nolimits z$ : principal branch of logarithm function, $\frac{\partial f}{\partial x}$ : partial derivative of $f$ with respect to $x$ , $\boldsymbol{{\Omega}}$ : a Riemann matrix, $u(x,y,t)$ : elevation and $c$ : complex constant
Referenced by:: §21.9
Permalink:: http://dlmf.nist.gov/21.9.E4
Encodings:: TeX, pMML, png

where $c$ is a complex constant and $\mathbf{k}$ , $\mathbf{l}$ , $\boldsymbol{{\omega}}$ , and $\boldsymbol{{\phi}}$ are $g$ -dimensional complex vectors; see Krichever (1976). These parameters, including $\boldsymbol{{\Omega}}$ , are not free: they are determined by a compact, connected Riemann surface (Krichever (1976)), or alternatively by an appropriate initial condition $u(x,y,0)$ (Deconinck and Segur (1998)). These solutions have been compared successfully with physical experiments for $g=1,2$ (Wiegel (1960), Hammack et al. (1989), and Hammack et al. (1995)). See Figures 21.9.1 and 21.9.2.

Figure 21.9.1: Two-dimensional periodic waves in a shallow water wave tank, taken from Hammack et al. (1995, p. 97) by permission of Cambridge University Press. The original caption reads “Mosaic of two overhead photographs, showing surface patterns of waves in shallow water.”

Referenced by:: §21.9
Permalink:: http://dlmf.nist.gov/21.9.F1
Encodings:: pdf, png

Figure 21.9.2: Contour plot of a two-phase solution of Equation (21.9.3). Such a solution is given in terms of a Riemann theta function with two phases; see Krichever (1976), Dubrovin (1981), and Hammack et al. (1995).

Referenced by:: §21.9
Permalink:: http://dlmf.nist.gov/21.9.F2
Encodings:: pdf, png

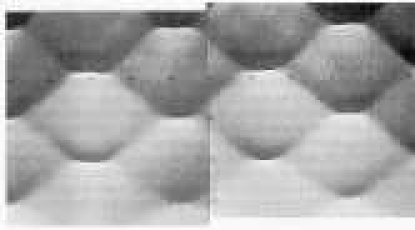
Furthermore, the solutions of the KP equation solve the Schottky problem: this is the question concerning conditions that a Riemann matrix needs to satisfy in order to be associated with a Riemann surface (Schottky (1903)). Following the work of Krichever (1976), Novikov conjectured that the Riemann theta function in (21.9.4) gives rise to a solution of the KP equation (21.9.3) if, and only if, the theta function originates from a Riemann surface; see Dubrovin (1981, §IV.4). The first part of this conjecture was established in Krichever (1976); the second part was proved in Shiota (1986).