variation of real or complex functions

SearchAdvancedHelp

(0.024 seconds)

31—40 of 603 matching pages

31: 4.28 Definitions and Periodicity

… ►

4.28.3 $$\cosh z\pm \sinh z={\mathrm{e}}^{\pm z},$$

ⓘ

Symbols:

$\mathrm{e}$: base of natural logarithm, $\cosh z$: hyperbolic cosine function, $\sinh z$: hyperbolic sine function and $z$: complex variable

A&S Ref:

4.5.19 4.5.20

Permalink:

http://dlmf.nist.gov/4.28.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §4.28 and Ch.4

… ►

4.28.5 $$\mathrm{csch}z=\frac{1}{\sinh z},$$

ⓘ

Defines:

$\mathrm{csch}z$: hyperbolic cosecant function

Symbols:

$\sinh z$: hyperbolic sine function and $z$: complex variable

A&S Ref:

4.5.4

Permalink:

http://dlmf.nist.gov/4.28.E5

Encodings:

pMML, png, TeX

See also:

Annotations for §4.28 and Ch.4

►

4.28.6 $$\mathrm{sech}z=\frac{1}{\cosh z},$$

ⓘ

Defines:

$\mathrm{sech}z$: hyperbolic secant function

Symbols:

$\cosh z$: hyperbolic cosine function and $z$: complex variable

A&S Ref:

4.5.5

Permalink:

http://dlmf.nist.gov/4.28.E6

Encodings:

pMML, png, TeX

See also:

Annotations for §4.28 and Ch.4

►

4.28.7 $$\coth z=\frac{1}{\tanh z}.$$

ⓘ

Defines:

$\coth z$: hyperbolic cotangent function

Symbols:

$\tanh z$: hyperbolic tangent function and $z$: complex variable

A&S Ref:

4.5.6

Referenced by:

§4.45(i), §4.45(ii)

Permalink:

http://dlmf.nist.gov/4.28.E7

Encodings:

pMML, png, TeX

See also:

Annotations for §4.28 and Ch.4

… ►

4.28.12 $$\sec \left(\mathrm{i}z\right)=\mathrm{sech}z,$$

ⓘ

Symbols:

$\mathrm{sech}z$: hyperbolic secant function, $\mathrm{i}$: imaginary unit, $\sec z$: secant function and $z$: complex variable

A&S Ref:

4.5.11

Permalink:

http://dlmf.nist.gov/4.28.E12

Encodings:

pMML, png, TeX

See also:

Annotations for §4.28, §4.28 and Ch.4

…

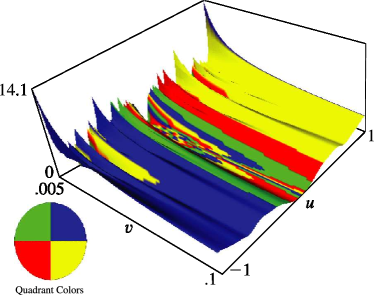
32: 20.3 Graphics

… ►

§20.3(ii) $\theta$-Functions: Complex Variable and Real Nome

… ►

§20.3(iii) $\theta$-Functions: Real Variable and Complex Lattice Parameter

… ►

►

►

Figure 20.3.21: ${\theta }_4\left(0\right|u+\mathrm{i}v)$, $-1\le u\le 1$, $0.005\le v\le 0.1$. Magnify 3D Help

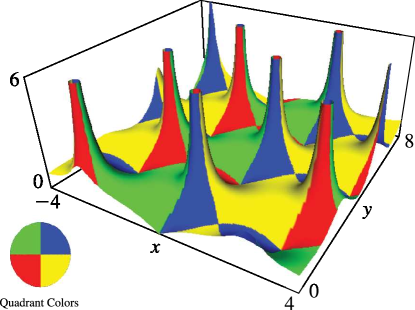
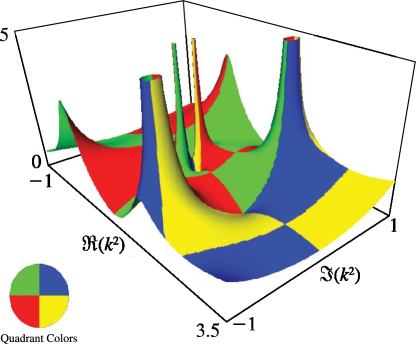
33: 22.3 Graphics

… ►

§22.3(iii) Complex $z$; Real $k$

… ►

§22.3(iv) Complex $k$

… ►

►

►

Figure 22.3.24: $\mathrm{sn}(x+\mathrm{i}y,k)$ for $-4\le x\le 4$, $0\le y\le 8$, $k=1+\frac{1}{2}\mathrm{i}$. … Magnify 3D Help

►

►

►

Figure 22.3.25: $\mathrm{sn}(5,k)$ as a function of complex $k^2$, $-1\le \mathrm{\Re }\left(k^2\right)\le 3.5$, $-1\le \mathrm{\Im }\left(k^2\right)\le 1$. … Magnify 3D Help

►

►►

Figure 22.3.26: Density plot of $|\mathrm{sn}(5,k)|$ as a function of complex $k^2$, $-10\le \mathrm{\Re }\left(k^2\right)\le 20$, $-10\le \mathrm{\Im }\left(k^2\right)\le 10$. … Magnify

…

34: 11.10 Anger–Weber Functions

… ►

11.10.6 $$f(\nu ,z)=\frac{(z-\nu )}{\pi z^2}\sin \left(\pi \nu \right),$$ $w={𝐉}_{\nu }\left(z\right)$,

ⓘ

Symbols:

${𝐉}_{\nu }\left(z\right)$: Anger function, $\pi$: the ratio of the circumference of a circle to its diameter, $\sin z$: sine function, $z$: complex variable and $\nu$: real or complex order

Permalink:

http://dlmf.nist.gov/11.10.E6

Encodings:

pMML, png, TeX

See also:

Annotations for §11.10(ii), §11.10 and Ch.11

… ►

11.10.7 $$f(\nu ,z)=-\frac{1}{\pi z^2}(z+\nu +(z-\nu )\cos \left(\pi \nu \right)),$$ $w={𝐄}_{\nu }\left(z\right)$.

ⓘ

Symbols:

${𝐄}_{\nu }\left(z\right)$: Weber function, $\pi$: the ratio of the circumference of a circle to its diameter, $\cos z$: cosine function, $z$: complex variable and $\nu$: real or complex order

Permalink:

http://dlmf.nist.gov/11.10.E7

Encodings:

pMML, png, TeX

See also:

Annotations for §11.10(ii), §11.10 and Ch.11

… ►

11.10.9 $${𝐄}_{\nu }\left(z\right)=\sin \left(\frac{1}{2}\pi \nu \right)S_1(\nu ,z)-\cos \left(\frac{1}{2}\pi \nu \right)S_2(\nu ,z),$$

ⓘ

Symbols:

${𝐄}_{\nu }\left(z\right)$: Weber function, $\pi$: the ratio of the circumference of a circle to its diameter, $\cos z$: cosine function, $\sin z$: sine function, $z$: complex variable and $\nu$: real or complex order

Referenced by:

(11.11.6)

Permalink:

http://dlmf.nist.gov/11.10.E9

Encodings:

pMML, png, TeX

See also:

Annotations for §11.10(iii), §11.10 and Ch.11

… ►

11.10.34 $$2{𝐉}_{\nu }^{\prime }\left(z\right)={𝐉}_{\nu -1}\left(z\right)-{𝐉}_{\nu +1}\left(z\right),$$

ⓘ

Symbols:

${𝐉}_{\nu }\left(z\right)$: Anger function, $z$: complex variable and $\nu$: real or complex order

Permalink:

http://dlmf.nist.gov/11.10.E34

Encodings:

pMML, png, TeX

See also:

Annotations for §11.10(ix), §11.10 and Ch.11

►

11.10.35 $$2{𝐄}_{\nu }^{\prime }\left(z\right)={𝐄}_{\nu -1}\left(z\right)-{𝐄}_{\nu +1}\left(z\right),$$

ⓘ

Symbols:

${𝐄}_{\nu }\left(z\right)$: Weber function, $z$: complex variable and $\nu$: real or complex order

Permalink:

http://dlmf.nist.gov/11.10.E35

Encodings:

pMML, png, TeX

See also:

Annotations for §11.10(ix), §11.10 and Ch.11

…

35: 4.34 Derivatives and Differential Equations

… ►

4.34.1 $$\frac{d}{dz}\sinh z=\cosh z,$$

ⓘ

Symbols:

$\frac{df}{dx}$: derivative of $f$ with respect to $x$ , $\cosh z$: hyperbolic cosine function, $\sinh z$: hyperbolic sine function and $z$: complex variable

A&S Ref:

4.5.71

Permalink:

http://dlmf.nist.gov/4.34.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §4.34 and Ch.4

►

4.34.2 $$\frac{d}{dz}\cosh z=\sinh z,$$

ⓘ

Symbols:

$\frac{df}{dx}$: derivative of $f$ with respect to $x$ , $\cosh z$: hyperbolic cosine function, $\sinh z$: hyperbolic sine function and $z$: complex variable

A&S Ref:

4.5.72

Permalink:

http://dlmf.nist.gov/4.34.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §4.34 and Ch.4

►

4.34.3 $$\frac{d}{dz}\tanh z={\mathrm{sech}}^{2}z,$$

ⓘ

Symbols:

$\frac{df}{dx}$: derivative of $f$ with respect to $x$ , $\mathrm{sech}z$: hyperbolic secant function, $\tanh z$: hyperbolic tangent function and $z$: complex variable

A&S Ref:

4.5.73

Permalink:

http://dlmf.nist.gov/4.34.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §4.34 and Ch.4

►

4.34.4 $$\frac{d}{dz}\mathrm{csch}z=-\mathrm{csch}z\coth z,$$

ⓘ

Symbols:

$\frac{df}{dx}$: derivative of $f$ with respect to $x$ , $\mathrm{csch}z$: hyperbolic cosecant function, $\coth z$: hyperbolic cotangent function and $z$: complex variable

A&S Ref:

4.5.74

Permalink:

http://dlmf.nist.gov/4.34.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §4.34 and Ch.4

►

4.34.5 $$\frac{d}{dz}\mathrm{sech}z=-\mathrm{sech}z\tanh z,$$

ⓘ

Symbols:

$\frac{df}{dx}$: derivative of $f$ with respect to $x$ , $\mathrm{sech}z$: hyperbolic secant function, $\tanh z$: hyperbolic tangent function and $z$: complex variable

A&S Ref:

4.5.75

Permalink:

http://dlmf.nist.gov/4.34.E5

Encodings:

pMML, png, TeX

See also:

Annotations for §4.34 and Ch.4

…

36: 4.14 Definitions and Periodicity

… ►

4.14.3 $$\cos z\pm \mathrm{i}\sin z={\mathrm{e}}^{\pm \mathrm{i}z},$$

ⓘ

Symbols:

$\cos z$: cosine function, $\mathrm{e}$: base of natural logarithm, $\mathrm{i}$: imaginary unit, $\sin z$: sine function and $z$: complex variable

Permalink:

http://dlmf.nist.gov/4.14.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §4.14 and Ch.4

►

4.14.4 $$\tan z=\frac{\sin z}{\cos z},$$

ⓘ

Defines:

$\tan z$: tangent function

Symbols:

$\cos z$: cosine function, $\sin z$: sine function and $z$: complex variable

A&S Ref:

4.3.3

Referenced by:

§4.14, §4.45(i)

Permalink:

http://dlmf.nist.gov/4.14.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §4.14 and Ch.4

►

4.14.5 $$\csc z=\frac{1}{\sin z},$$

ⓘ

Defines:

$\csc z$: cosecant function

Symbols:

$\sin z$: sine function and $z$: complex variable

A&S Ref:

4.3.4

Permalink:

http://dlmf.nist.gov/4.14.E5

Encodings:

pMML, png, TeX

See also:

Annotations for §4.14 and Ch.4

►

4.14.6 $$\sec z=\frac{1}{\cos z},$$

ⓘ

Defines:

$\sec z$: secant function

Symbols:

$\cos z$: cosine function and $z$: complex variable

A&S Ref:

4.3.5

Permalink:

http://dlmf.nist.gov/4.14.E6

Encodings:

pMML, png, TeX

See also:

Annotations for §4.14 and Ch.4

►

4.14.7 $$\cot z=\frac{\cos z}{\sin z}=\frac{1}{\tan z}.$$

ⓘ

Defines:

$\cot z$: cotangent function

Symbols:

$\cos z$: cosine function, $\sin z$: sine function, $\tan z$: tangent function and $z$: complex variable

A&S Ref:

4.3.6

Referenced by:

§4.14, §4.45(i), §4.45(ii)

Permalink:

http://dlmf.nist.gov/4.14.E7

Encodings:

pMML, png, TeX

See also:

Annotations for §4.14 and Ch.4

…

37: 22.11 Fourier and Hyperbolic Series

… ►

22.11.7 $$\mathrm{ns}(z,k)-\frac{\pi }{2K}\csc \zeta =\frac{2\pi }{K}\sum _{n=0}^{\mathrm{\infty }}\frac{q^{2n+1}\sin \left((2n+1)\zeta \right)}{1-q^{2n+1}},$$

ⓘ

Symbols:

$\mathrm{ns}(z,k)$: Jacobian elliptic function, $\pi$: the ratio of the circumference of a circle to its diameter, $K\left(k\right)$: Legendre’s complete elliptic integral of the first kind, $\csc z$: cosecant function, $q$: nome, $\sin z$: sine function, $z$: complex, $k$: modulus and $\zeta$: change of variable

A&S Ref:

16.23.10

Referenced by:

§22.11

Permalink:

http://dlmf.nist.gov/22.11.E7

Encodings:

pMML, png, TeX

See also:

Annotations for §22.11 and Ch.22

►

22.11.8 $$\mathrm{ds}(z,k)-\frac{\pi }{2K}\csc \zeta =-\frac{2\pi }{K}\sum _{n=0}^{\mathrm{\infty }}\frac{q^{2n+1}\sin \left((2n+1)\zeta \right)}{1+q^{2n+1}},$$

ⓘ

Symbols:

$\mathrm{ds}(z,k)$: Jacobian elliptic function, $\pi$: the ratio of the circumference of a circle to its diameter, $K\left(k\right)$: Legendre’s complete elliptic integral of the first kind, $\csc z$: cosecant function, $q$: nome, $\sin z$: sine function, $z$: complex, $k$: modulus and $\zeta$: change of variable

A&S Ref:

16.23.11

Permalink:

http://dlmf.nist.gov/22.11.E8

Encodings:

pMML, png, TeX

See also:

Annotations for §22.11 and Ch.22

►

22.11.9 $$\mathrm{cs}(z,k)-\frac{\pi }{2K}\cot \zeta =-\frac{2\pi }{K}\sum _{n=1}^{\mathrm{\infty }}\frac{q^{2n}\sin \left(2n\zeta \right)}{1+q^{2n}},$$

ⓘ

Symbols:

$\mathrm{cs}(z,k)$: Jacobian elliptic function, $\pi$: the ratio of the circumference of a circle to its diameter, $K\left(k\right)$: Legendre’s complete elliptic integral of the first kind, $\cot z$: cotangent function, $q$: nome, $\sin z$: sine function, $z$: complex, $k$: modulus and $\zeta$: change of variable

A&S Ref:

16.23.12

Permalink:

http://dlmf.nist.gov/22.11.E9

Encodings:

pMML, png, TeX

See also:

Annotations for §22.11 and Ch.22

►

22.11.10 $$\mathrm{dc}(z,k)-\frac{\pi }{2K}\sec \zeta =\frac{2\pi }{K}\sum _{n=0}^{\mathrm{\infty }}\frac{{(-1)}^n{q}^{2n+1}\cos \left((2n+1)\zeta \right)}{1-q^{2n+1}},$$

ⓘ

Symbols:

$\mathrm{dc}(z,k)$: Jacobian elliptic function, $\pi$: the ratio of the circumference of a circle to its diameter, $K\left(k\right)$: Legendre’s complete elliptic integral of the first kind, $\cos z$: cosine function, $q$: nome, $\sec z$: secant function, $z$: complex, $k$: modulus and $\zeta$: change of variable

A&S Ref:

16.23.7

Permalink:

http://dlmf.nist.gov/22.11.E10

Encodings:

pMML, png, TeX

See also:

Annotations for §22.11 and Ch.22

… ►

22.11.12 $$\mathrm{sc}(z,k)-\frac{\pi }{2K{k}^{\prime }}\tan \zeta =\frac{2\pi }{K{k}^{\prime }}\sum _{n=1}^{\mathrm{\infty }}\frac{{(-1)}^n{q}^{2n}\sin \left(2n\zeta \right)}{1+q^{2n}}.$$

ⓘ

Symbols:

$\mathrm{sc}(z,k)$: Jacobian elliptic function, $\pi$: the ratio of the circumference of a circle to its diameter, $K\left(k\right)$: Legendre’s complete elliptic integral of the first kind, $q$: nome, $\sin z$: sine function, $\tan z$: tangent function, $z$: complex, $k$: modulus, $k^{\prime }$: complementary modulus and $\zeta$: change of variable

A&S Ref:

16.23.9

Referenced by:

§22.11

Permalink:

http://dlmf.nist.gov/22.11.E12

Encodings:

pMML, png, TeX

See also:

Annotations for §22.11 and Ch.22

…

38: 31.3 Basic Solutions

… ►

31.3.5 $$z^{1-\gamma }H\mathrm{\ell }(a,(a\delta +ϵ)(1-\gamma )+q;\alpha +1-\gamma ,\beta +1-\gamma ,2-\gamma ,\delta ;z).$$

ⓘ

Symbols:

$H\mathrm{\ell }(a,q;\alpha ,\beta ,\gamma ,\delta ;z)$: Heun functions, $z$: complex variable, $\gamma$: real or complex parameter, $\delta$: real or complex parameter, $ϵ$: real or complex parameter, $a$: complex parameter, $q$: real or complex parameter, $\alpha$: real or complex parameter and $\beta$: real or complex parameter

Referenced by:

§31.3(iii), §31.7(ii)

Permalink:

http://dlmf.nist.gov/31.3.E5

Encodings:

pMML, png, TeX

See also:

Annotations for §31.3(i), §31.3 and Ch.31

… ►

31.3.6 $$H\mathrm{\ell }(1-a,\alpha \beta -q;\alpha ,\beta ,\delta ,\gamma ;1-z),$$

ⓘ

Symbols:

$H\mathrm{\ell }(a,q;\alpha ,\beta ,\gamma ,\delta ;z)$: Heun functions, $z$: complex variable, $\gamma$: real or complex parameter, $\delta$: real or complex parameter, $a$: complex parameter, $q$: real or complex parameter, $\alpha$: real or complex parameter and $\beta$: real or complex parameter

Permalink:

http://dlmf.nist.gov/31.3.E6

Encodings:

pMML, png, TeX

See also:

Annotations for §31.3(ii), §31.3 and Ch.31

►

31.3.7 $${(1-z)}^{1-\delta }H\mathrm{\ell }(1-a,((1-a)\gamma +ϵ)(1-\delta )+\alpha \beta -q;\alpha +1-\delta ,\beta +1-\delta ,2-\delta ,\gamma ;1-z).$$

ⓘ

Symbols:

$H\mathrm{\ell }(a,q;\alpha ,\beta ,\gamma ,\delta ;z)$: Heun functions, $z$: complex variable, $\gamma$: real or complex parameter, $\delta$: real or complex parameter, $ϵ$: real or complex parameter, $a$: complex parameter, $q$: real or complex parameter, $\alpha$: real or complex parameter and $\beta$: real or complex parameter

Permalink:

http://dlmf.nist.gov/31.3.E7

Encodings:

pMML, png, TeX

See also:

Annotations for §31.3(ii), §31.3 and Ch.31

… ►

31.3.8 $$H\mathrm{\ell }(\frac{a}{a-1},\frac{\alpha \beta a-q}{a-1};\alpha ,\beta ,ϵ,\delta ;\frac{a-z}{a-1}),$$

ⓘ

Symbols:

$H\mathrm{\ell }(a,q;\alpha ,\beta ,\gamma ,\delta ;z)$: Heun functions, $z$: complex variable, $\delta$: real or complex parameter, $ϵ$: real or complex parameter, $a$: complex parameter, $q$: real or complex parameter, $\alpha$: real or complex parameter and $\beta$: real or complex parameter

Permalink:

http://dlmf.nist.gov/31.3.E8

Encodings:

pMML, png, TeX

See also:

Annotations for §31.3(ii), §31.3 and Ch.31

… ►

31.3.12 $$H\mathrm{\ell }(1/a,q/a;\alpha ,\beta ,\gamma ,\alpha +\beta +1-\gamma -\delta ;z/a),$$

ⓘ

Symbols:

$H\mathrm{\ell }(a,q;\alpha ,\beta ,\gamma ,\delta ;z)$: Heun functions, $z$: complex variable, $\gamma$: real or complex parameter, $\delta$: real or complex parameter, $a$: complex parameter, $q$: real or complex parameter, $\alpha$: real or complex parameter and $\beta$: real or complex parameter

Permalink:

http://dlmf.nist.gov/31.3.E12

Encodings:

pMML, png, TeX

See also:

Annotations for §31.3(iii), §31.3 and Ch.31

…

39: 17.5 ${}_0{}^{}\varphi _0^{},{}_1{}^{}\varphi _0^{},{}_1{}^{}\varphi _1^{}$ Functions

… ►

17.5.1 $${}_0{}^{}\varphi _0^{}(-;-;q,z)=\sum _{n=0}^{\mathrm{\infty }}\frac{{(-1)}^n{q}^{\left(\genfrac{}{}{0.0pt}{}{n}{2}\right)}{z}^n}{{(q;q)}_n}={(z;q)}_{\mathrm{\infty }};$$

ⓘ

Symbols:

$\left(\genfrac{}{}{0.0pt}{}{m}{n}\right)$: binomial coefficient, ${(a;q)}_n$: $q$-Pochhammer symbol (or $q$-shifted factorial), ${}_{r+1}{}^{}\varphi _s^{}(a_0,\mathrm{\dots },a_r;b_1,\mathrm{\dots },b_s;q,z)$ or ${}_{r+1}{}^{}\varphi _s^{}(\genfrac{}{}{0pt}{}{a_0,\mathrm{\dots },a_r}{b_1,\mathrm{\dots },b_s};q,z)$: basic hypergeometric (or $q$-hypergeometric) function, $q$: complex base, $n$: nonnegative integer and $z$: complex variable

Referenced by:

§17.2(iii), Erratum (V1.1.11) for Equation (17.5.1)

Permalink:

http://dlmf.nist.gov/17.5.E1

Encodings:

pMML, png, TeX

Correction (effective with 1.1.11):

The constraint is not necessary and was removed.

See also:

Annotations for §17.5, §17.5 and Ch.17

… ►

17.5.2 $${}_1{}^{}\varphi _0^{}(a;-;q,z)=\frac{{(az;q)}_{\mathrm{\infty }}}{{(z;q)}_{\mathrm{\infty }}},$$ ;

ⓘ

Symbols:

${(a;q)}_n$: $q$-Pochhammer symbol (or $q$-shifted factorial), ${}_{r+1}{}^{}\varphi _s^{}(a_0,\mathrm{\dots },a_r;b_1,\mathrm{\dots },b_s;q,z)$ or ${}_{r+1}{}^{}\varphi _s^{}(\genfrac{}{}{0pt}{}{a_0,\mathrm{\dots },a_r}{b_1,\mathrm{\dots },b_s};q,z)$: basic hypergeometric (or $q$-hypergeometric) function, $q$: complex base and $z$: complex variable

Permalink:

http://dlmf.nist.gov/17.5.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §17.5, §17.5 and Ch.17

… ►

17.5.3 $${}_1{}^{}\varphi _0^{}(q^{-n};-;q,z)={(z{q}^{-n};q)}_n.$$

ⓘ

Symbols:

${(a;q)}_n$: $q$-Pochhammer symbol (or $q$-shifted factorial), ${}_{r+1}{}^{}\varphi _s^{}(a_0,\mathrm{\dots },a_r;b_1,\mathrm{\dots },b_s;q,z)$ or ${}_{r+1}{}^{}\varphi _s^{}(\genfrac{}{}{0pt}{}{a_0,\mathrm{\dots },a_r}{b_1,\mathrm{\dots },b_s};q,z)$: basic hypergeometric (or $q$-hypergeometric) function, $q$: complex base, $n$: nonnegative integer and $z$: complex variable

Permalink:

http://dlmf.nist.gov/17.5.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §17.5, §17.5 and Ch.17

… ►

17.5.4 $${}_1{}^{}\varphi _0^{}(0;-;q,z)=\sum _{n=0}^{\mathrm{\infty }}\frac{z^n}{{(q;q)}_n}=\frac{1}{{(z;q)}_{\mathrm{\infty }}},$$ ;

ⓘ

Symbols:

${(a;q)}_n$: $q$-Pochhammer symbol (or $q$-shifted factorial), ${}_{r+1}{}^{}\varphi _s^{}(a_0,\mathrm{\dots },a_r;b_1,\mathrm{\dots },b_s;q,z)$ or ${}_{r+1}{}^{}\varphi _s^{}(\genfrac{}{}{0pt}{}{a_0,\mathrm{\dots },a_r}{b_1,\mathrm{\dots },b_s};q,z)$: basic hypergeometric (or $q$-hypergeometric) function, $q$: complex base, $n$: nonnegative integer and $z$: complex variable

Referenced by:

§17.2(iii)

Permalink:

http://dlmf.nist.gov/17.5.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §17.5, §17.5 and Ch.17

… ►

17.5.5 $${}_1{}^{}\varphi _1^{}(\genfrac{}{}{0pt}{}{a}{c};q,c/a)=\frac{{(c/a;q)}_{\mathrm{\infty }}}{{(c;q)}_{\mathrm{\infty }}}.$$

ⓘ

Symbols:

${(a;q)}_n$: $q$-Pochhammer symbol (or $q$-shifted factorial), ${}_{r+1}{}^{}\varphi _s^{}(a_0,\mathrm{\dots },a_r;b_1,\mathrm{\dots },b_s;q,z)$ or ${}_{r+1}{}^{}\varphi _s^{}(\genfrac{}{}{0pt}{}{a_0,\mathrm{\dots },a_r}{b_1,\mathrm{\dots },b_s};q,z)$: basic hypergeometric (or $q$-hypergeometric) function and $q$: complex base

Referenced by:

Erratum (V1.1.10) for Equation (17.5.5)

Permalink:

http://dlmf.nist.gov/17.5.E5

Encodings:

pMML, png, TeX

Correction (effective with 1.1.10):

The constraint is not necessary and was removed.

See also:

Annotations for §17.5, §17.5 and Ch.17

40: 20.7 Identities

… ►

20.7.1 $${\theta }_3^2(0,q){\theta }_3^2(z,q)={\theta }_4^2(0,q){\theta }_4^2(z,q)+{\theta }_2^2(0,q){\theta }_2^2(z,q),$$

ⓘ

Symbols:

${\theta }_j(z,q)$: theta function, $z$: complex and $q$: nome

A&S Ref:

16.28.3

Permalink:

http://dlmf.nist.gov/20.7.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §20.7(i), §20.7 and Ch.20

►

20.7.2 $${\theta }_3^2(0,q){\theta }_4^2(z,q)={\theta }_2^2(0,q){\theta }_1^2(z,q)+{\theta }_4^2(0,q){\theta }_3^2(z,q),$$

ⓘ

Symbols:

${\theta }_j(z,q)$: theta function, $z$: complex and $q$: nome

A&S Ref:

16.28.2

Permalink:

http://dlmf.nist.gov/20.7.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §20.7(i), §20.7 and Ch.20

►

20.7.3 $${\theta }_2^2(0,q){\theta }_4^2(z,q)={\theta }_3^2(0,q){\theta }_1^2(z,q)+{\theta }_4^2(0,q){\theta }_2^2(z,q),$$

ⓘ

Symbols:

${\theta }_j(z,q)$: theta function, $z$: complex and $q$: nome

A&S Ref:

16.28.1

Permalink:

http://dlmf.nist.gov/20.7.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §20.7(i), §20.7 and Ch.20

… ►

20.7.28 $${\theta }_3\left(z\right|\tau +1)={\theta }_4\left(z\right|\tau ),$$

ⓘ

Symbols:

${\theta }_j\left(z\right|\tau )$: theta function, $z$: complex and $\tau$: lattice parameter

Permalink:

http://dlmf.nist.gov/20.7.E28

Encodings:

pMML, png, TeX

See also:

Annotations for §20.7(viii), §20.7 and Ch.20

►

20.7.29 $${\theta }_4\left(z\right|\tau +1)={\theta }_3\left(z\right|\tau ).$$

ⓘ

Symbols:

${\theta }_j\left(z\right|\tau )$: theta function, $z$: complex and $\tau$: lattice parameter

Permalink:

http://dlmf.nist.gov/20.7.E29

Encodings:

pMML, png, TeX

See also:

Annotations for §20.7(viii), §20.7 and Ch.20

…