two or more variables

SearchAdvancedHelp

(0.004 seconds)

1—10 of 286 matching pages

1: 18.37 Classical OP’s in Two or More Variables

§18.37 Classical OP’s in Two or More Variables

…

2: 1.5 Calculus of Two or More Variables

§1.5 Calculus of Two or More Variables

►

§1.5(i) Partial Derivatives

… ►

1.5.1 $$\underset{(x,y)\to (a,b)}{lim}f(x,y)=f(a,b),$$

ⓘ

Symbols:

$(a,b)$: open interval

Referenced by:

§1.9(ii)

Permalink:

http://dlmf.nist.gov/1.5.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §1.5(i), §1.5 and Ch.1

… ►

§1.5(iii) Taylor’s Theorem; Maxima and Minima

… ►

3: 35.2 Laplace Transform

… ►where the integration variable $𝐗$ ranges over the space $𝛀$. …

4: 21.8 Abelian Functions

… ►In consequence, Abelian functions are generalizations of elliptic functions (§23.2(iii)) to more than one complex variable. …

5: 19.23 Integral Representations

… ►

19.23.3 $$R_D(0,y,z)=3{\int }_0^{\pi /2}{(y{\cos }^2\theta +z{\sin }^2\theta )}^{-3/2}{\sin }^2\theta d\theta .$$

ⓘ

Symbols:

$R_D(x,y,z)$: elliptic integral symmetric in only two variables, $\pi$: the ratio of the circumference of a circle to its diameter, $\cos z$: cosine function, $dx$: differential of $x$ , $\int$: integral and $\sin z$: sine function

Referenced by:

§19.23, §19.23

Permalink:

http://dlmf.nist.gov/19.23.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §19.23 and Ch.19

… ►In (19.23.8)–(19.23.10) one or more of the variables may be 0 if the integral converges. …

6: Errata

… ►

The wording was changed to make the integration variable more apparent.

… ►

The symbol $\sim$ is used for two purposes in the DLMF, in some cases for asymptotic equality and in other cases for asymptotic expansion, but links to the appropriate definitions were not provided. In this release changes have been made to provide these links.

►

A short paragraph dealing with asymptotic approximations that are expressed in terms of two or more Poincaré asymptotic expansions has been added below (2.1.16).

… ►

Originally used $f(x)$ to represent both $U(-c,x)$ and $\overline{U}(-c,x)$. This has been replaced by two equations giving explicit definitions for the two envelope functions. Some slight changes in wording were needed to make this clear to readers.

… ►

This figure was rescaled, with symmetry lines added, to make evident the symmetry due to the inverse relationship between the two functions.

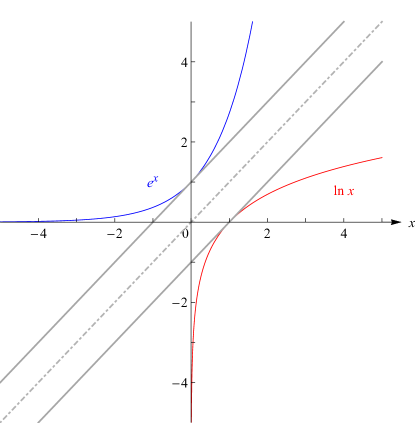
Reported 2015-11-12 by James W. Pitman.

…

7: Sidebar 21.SB2: A two-phase solution of the Kadomtsev–Petviashvili equation (21.9.3)

Sidebar 21.SB2: A two-phase solution of the Kadomtsev–Petviashvili equation (21.9.3)

… ►A two-phase solution of the Kadomtsev–Petviashvili equation (21.9.3). Such a solution is given in terms of a Riemann theta function with two phases. …The agreement of these solutions with two-dimensional surface water waves in shallow water was considered in Hammack et al. (1989, 1995).

8: Sidebar 21.SB1: Periodic Surface Waves

… ►Two-dimensional periodic waves in a shallow water wave tank. Taken from Joe Hammack, Daryl McCallister, Norman Scheffner and Harvey Segur, “Two-dimensional periodic waves in shallow water. …The caption reads “Mosaic of two overhead photographs, showing surface patterns of waves in shallow water”. …

9: 33.22 Particle Scattering and Atomic and Molecular Spectra

… ►With $\mathrm{e}$ denoting here the elementary charge, the Coulomb potential between two point particles with charges $Z_1\mathrm{e},Z_2\mathrm{e}$ and masses $m_1,m_2$ separated by a distance $s$ is $V(s)=Z_1{Z}_2{\mathrm{e}}^2/(4\pi {\epsilon }_{0}s)=Z_1{Z}_2\alpha \mathrm{\hslash }c/s$, where $Z_j$ are atomic numbers, ${\epsilon }_0$ is the electric constant, $\alpha$ is the fine structure constant, and $\mathrm{\hslash }$ is the reduced Planck’s constant. … ►In these applications, the $Z$-scaled variables $r$ and $ϵ$ are more convenient. …

10: 31.17 Physical Applications

… ►The problem of adding three quantum spins $𝐬$, $𝐭$, and $𝐮$ can be solved by the method of separation of variables, and the solution is given in terms of a product of two Heun functions. … ►For more details about the method of separation of variables and relation to special functions see Olevskiĭ (1950), Kalnins et al. (1976), Miller (1977), and Kalnins (1986). … ►More applications—including those of generalized spheroidal wave functions and confluent Heun functions in mathematical physics, astrophysics, and the two-center problem in molecular quantum mechanics—can be found in Leaver (1986) and Slavyanov and Lay (2000, Chapter 4). …