real part

SearchAdvancedHelp

(0.008 seconds)

21—30 of 249 matching pages

21: 12.12 Integrals

… ►

12.12.1 $${\int }_0^{\mathrm{\infty }}{\mathrm{e}}^{-\frac{1}{4}{t}^2}{t}^{\mu -1}U(a,t)dt=\frac{\sqrt{\pi }{2}^{-\frac{1}{2}(\mu +a+\frac{1}{2})}\mathrm{\Gamma }\left(\mu \right)}{\mathrm{\Gamma }\left(\frac{1}{2}(\mu +a+\frac{3}{2})\right)},$$ $\mathrm{\Re }\mu >0$ ,

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $\pi$: the ratio of the circumference of a circle to its diameter, $dx$: differential of $x$ , $\mathrm{e}$: base of natural logarithm, $\int$: integral, $U(a,z)$: parabolic cylinder function, $\mathrm{\Re }$: real part and $a$: real or complex parameter

Permalink:

http://dlmf.nist.gov/12.12.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §12.12 and Ch.12

►

12.12.2 $${\int }_0^{\mathrm{\infty }}{\mathrm{e}}^{-\frac{3}{4}{t}^2}{t}^{-a-\frac{3}{2}}U(a,t)dt=2^{\frac{1}{4}+\frac{1}{2}a}\mathrm{\Gamma }\left(-a-\frac{1}{2}\right)\cos \left((\frac{1}{4}a+\frac{1}{8})\pi \right),$$ ,

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $\pi$: the ratio of the circumference of a circle to its diameter, $\cos z$: cosine function, $dx$: differential of $x$ , $\mathrm{e}$: base of natural logarithm, $\int$: integral, $U(a,z)$: parabolic cylinder function, $\mathrm{\Re }$: real part and $a$: real or complex parameter

Permalink:

http://dlmf.nist.gov/12.12.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §12.12 and Ch.12

►

12.12.3 $${\int }_0^{\mathrm{\infty }}{\mathrm{e}}^{-\frac{1}{4}{t}^2}{t}^{-a-\frac{1}{2}}{(x^2+t^2)}^{-1}U(a,t)dt=\sqrt{\pi /2}\mathrm{\Gamma }\left(\frac{1}{2}-a\right)x^{-a-\frac{3}{2}}{\mathrm{e}}^{\frac{1}{4}{x}^2}U(-a,x),$$ .

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $\pi$: the ratio of the circumference of a circle to its diameter, $dx$: differential of $x$ , $\mathrm{e}$: base of natural logarithm, $\int$: integral, $U(a,z)$: parabolic cylinder function, $\mathrm{\Re }$: real part, $x$: real variable and $a$: real or complex parameter

Permalink:

http://dlmf.nist.gov/12.12.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §12.12 and Ch.12

… ►

12.12.4 $${(U(a,z))}^2+{(\overline{U}(a,z))}^2=\frac{2^{\frac{3}{2}}}{\pi }\mathrm{\Gamma }\left(\frac{1}{2}-a\right){\int }_0^{\mathrm{\infty }}\frac{{\mathrm{e}}^{2at+\frac{1}{2}{z}^2\tanh t}}{\sqrt{\sinh \left(2t\right)}}dt,$$ .

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $\pi$: the ratio of the circumference of a circle to its diameter, $dx$: differential of $x$ , $\mathrm{e}$: base of natural logarithm, $\sinh z$: hyperbolic sine function, $\tanh z$: hyperbolic tangent function, $\int$: integral, $U(a,z)$: parabolic cylinder function, $\overline{U}(a,x)$: parabolic cylinder function, $\mathrm{\Re }$: real part, $z$: complex variable and $a$: real or complex parameter

Notes:

See Durand (1975).

Referenced by:

§12.12

Permalink:

http://dlmf.nist.gov/12.12.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §12.12, §12.12 and Ch.12

…

22: 5.12 Beta Function

… ►In (5.12.1)–(5.12.4) it is assumed $\mathrm{\Re }a>0$ and $\mathrm{\Re }b>0$. … ►

5.12.7 $${\int }_0^{\mathrm{\infty }}\frac{\cosh \left(2bt\right)}{{(\cosh t)}^{2a}}dt=4^{a-1}\mathrm{B}(a+b,a-b),$$ $\mathrm{\Re }a>|\mathrm{\Re }b|$.

ⓘ

Symbols:

$\mathrm{B}(a,b)$: beta function, $dx$: differential of $x$ , $\cosh z$: hyperbolic cosine function, $\int$: integral, $\mathrm{\Re }$: real part, $a$: real or complex variable and $b$: real or complex variable

Referenced by:

§5.12

Permalink:

http://dlmf.nist.gov/5.12.E7

Encodings:

pMML, png, TeX

See also:

Annotations for §5.12, §5.12 and Ch.5

►

5.12.8 $$\frac{1}{2\pi }{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\frac{dt}{{(w+\mathrm{i}t)}^a{(z-\mathrm{i}t)}^b}=\frac{{(w+z)}^{1-a-b}}{(a+b-1)\mathrm{B}(a,b)},$$ $\mathrm{\Re }\left(a+b\right)>1$, $\mathrm{\Re }w>0$, $\mathrm{\Re }z>0$.

ⓘ

Symbols:

$\mathrm{B}(a,b)$: beta function, $\pi$: the ratio of the circumference of a circle to its diameter, $dx$: differential of $x$ , $\mathrm{i}$: imaginary unit, $\int$: integral, $\mathrm{\Re }$: real part, $w$: real or complex variable, $z$: complex variable, $a$: real or complex variable and $b$: real or complex variable

Referenced by:

§5.12, §5.12

Permalink:

http://dlmf.nist.gov/5.12.E8

Encodings:

pMML, png, TeX

See also:

Annotations for §5.12, §5.12 and Ch.5

… ►

5.12.9 $$\frac{1}{2\pi \mathrm{i}}{\int }_{c-\mathrm{\infty }\mathrm{i}}^{c+\mathrm{\infty }\mathrm{i}}{t}^{-a}{(1-t)}^{-1-b}dt=\frac{1}{b\mathrm{B}(a,b)},$$ , $\mathrm{\Re }\left(a+b\right)>0$.

ⓘ

Symbols:

$\mathrm{B}(a,b)$: beta function, $\pi$: the ratio of the circumference of a circle to its diameter, $dx$: differential of $x$ , $\mathrm{i}$: imaginary unit, $\int$: integral, $\mathrm{\Re }$: real part, $a$: real or complex variable and $b$: real or complex variable

Referenced by:

§5.12

Permalink:

http://dlmf.nist.gov/5.12.E9

Encodings:

pMML, png, TeX

See also:

Annotations for §5.12, §5.12 and Ch.5

… ►when $\mathrm{\Re }b>0$, $a$ is not an integer and the contour cuts the real axis between $-1$ and the origin. …

23: 19.3 Graphics

… ►

►

►

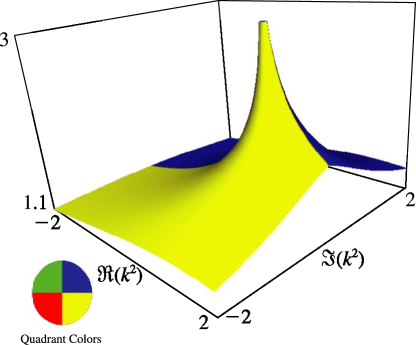
Figure 19.3.7: $K\left(k\right)$ as a function of complex $k^2$ for $-2\le \mathrm{\Re }\left(k^2\right)\le 2$, $-2\le \mathrm{\Im }\left(k^2\right)\le 2$. … Magnify 3D Help

… ►

►

►

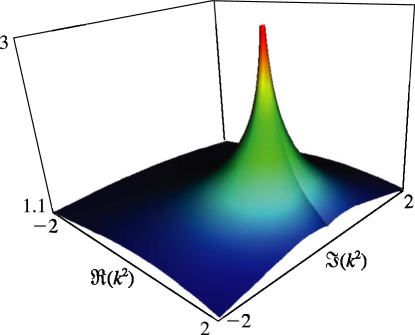
Figure 19.3.9: $\mathrm{\Re }\left(K\left(k\right)\right)$ as a function of complex $k^2$ for $-2\le \mathrm{\Re }\left(k^2\right)\le 2$, $-2\le \mathrm{\Im }\left(k^2\right)\le 2$. The real part is symmetric under reflection in the real axis. … Magnify 3D Help

… ►

►

►

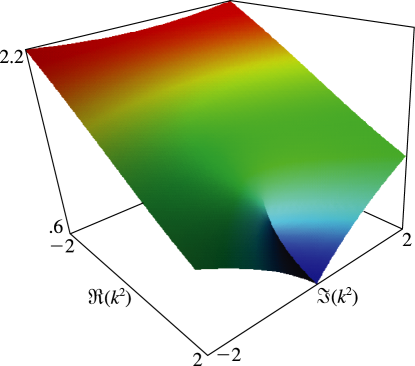
Figure 19.3.11: $\mathrm{\Re }\left(E\left(k\right)\right)$ as a function of complex $k^2$ for $-2\le \mathrm{\Re }\left(k^2\right)\le 2$, $-2\le \mathrm{\Im }\left(k^2\right)\le 2$. The real part is symmetric under reflection in the real axis. … Magnify 3D Help

…

24: 8.6 Integral Representations

… ►

8.6.2 $$\gamma (a,z)=z^{\frac{1}{2}a}{\int }_0^{\mathrm{\infty }}{\mathrm{e}}^{-t}{t}^{\frac{1}{2}a-1}{J}_a\left(2\sqrt{zt}\right)dt,$$ $\mathrm{\Re }a>0$.

ⓘ

Symbols:

$J_{\nu }\left(z\right)$: Bessel function of the first kind, $dx$: differential of $x$ , $\mathrm{e}$: base of natural logarithm, $\gamma (a,z)$: incomplete gamma function, $\int$: integral, $\mathrm{\Re }$: real part, $z$: complex variable and $a$: parameter

Referenced by:

§8.6(i)

Permalink:

http://dlmf.nist.gov/8.6.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §8.6(i), §8.6 and Ch.8

►

8.6.3 $$\gamma (a,z)=z^a{\int }_0^{\mathrm{\infty }}\exp \left(-at-z{\mathrm{e}}^{-t}\right)dt,$$ $\mathrm{\Re }a>0$.

ⓘ

Symbols:

$dx$: differential of $x$ , $\exp z$: exponential function, $\mathrm{e}$: base of natural logarithm, $\gamma (a,z)$: incomplete gamma function, $\int$: integral, $\mathrm{\Re }$: real part, $z$: complex variable and $a$: parameter

Referenced by:

§8.6(i)

Permalink:

http://dlmf.nist.gov/8.6.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §8.6(i), §8.6 and Ch.8

… ►

8.6.5 $$\mathrm{\Gamma }(a,z)=z^a{\mathrm{e}}^{-z}{\int }_0^{\mathrm{\infty }}\frac{{\mathrm{e}}^{-zt}}{{(1+t)}^{1-a}}dt,$$ $\mathrm{\Re }z>0$,

ⓘ

Symbols:

$dx$: differential of $x$ , $\mathrm{e}$: base of natural logarithm, $\mathrm{\Gamma }(a,z)$: incomplete gamma function, $\int$: integral, $\mathrm{\Re }$: real part, $z$: complex variable and $a$: parameter

Referenced by:

§8.6(i), (8.7.6)

Permalink:

http://dlmf.nist.gov/8.6.E5

Encodings:

pMML, png, TeX

See also:

Annotations for §8.6(i), §8.6 and Ch.8

… ►

8.6.7 $$\mathrm{\Gamma }(a,z)=z^a{\int }_0^{\mathrm{\infty }}\exp \left(at-z{\mathrm{e}}^t\right)dt,$$ $\mathrm{\Re }z>0$.

ⓘ

Symbols:

$dx$: differential of $x$ , $\exp z$: exponential function, $\mathrm{e}$: base of natural logarithm, $\mathrm{\Gamma }(a,z)$: incomplete gamma function, $\int$: integral, $\mathrm{\Re }$: real part, $z$: complex variable and $a$: parameter

Referenced by:

§8.6(i)

Permalink:

http://dlmf.nist.gov/8.6.E7

Encodings:

pMML, png, TeX

See also:

Annotations for §8.6(i), §8.6 and Ch.8

… ►

8.6.9 $$\mathrm{\Gamma }(-a,z{\mathrm{e}}^{\pm \pi \mathrm{i}})=\frac{{\mathrm{e}}^z{\mathrm{e}}^{\mp \pi \mathrm{i}a}}{\mathrm{\Gamma }\left(1+a\right)}{\int }_0^{\mathrm{\infty }}\frac{t^a{\mathrm{e}}^{-zt}}{t-1}dt,$$ $\mathrm{\Re }z>0$, $\mathrm{\Re }a>-1$,

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $\pi$: the ratio of the circumference of a circle to its diameter, $dx$: differential of $x$ , $\mathrm{e}$: base of natural logarithm, $\mathrm{i}$: imaginary unit, $\mathrm{\Gamma }(a,z)$: incomplete gamma function, $\int$: integral, $\mathrm{\Re }$: real part, $z$: complex variable and $a$: parameter

Referenced by:

§8.6(ii)

Permalink:

http://dlmf.nist.gov/8.6.E9

Encodings:

pMML, png, TeX

See also:

Annotations for §8.6(ii), §8.6 and Ch.8

…

25: 11.7 Integrals and Sums

… ►

11.7.6 $$f_{\nu +1}(z)=(2\nu +1)f_{\nu }(z)-z^{\nu +1}{𝐇}_{\nu }\left(z\right)+\frac{{(\frac{1}{2}{z}^2)}^{\nu +1}}{(\nu +1)\sqrt{\pi }\mathrm{\Gamma }\left(\nu +\frac{3}{2}\right)},$$ $\mathrm{\Re }\nu >-1$.

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, ${𝐇}_{\nu }\left(z\right)$: Struve function, $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{\Re }$: real part, $z$: complex variable and $\nu$: real or complex order

A&S Ref:

12.1.28 (The condition on $\nu$ has been corrected.)

Permalink:

http://dlmf.nist.gov/11.7.E6

Encodings:

pMML, png, TeX

See also:

Annotations for §11.7(i), §11.7 and Ch.11

… ►

11.7.9 $${\int }_0^{\mathrm{\infty }}{𝐇}_{\nu }\left(t\right)dt=-\cot \left(\frac{1}{2}\pi \nu \right),$$ ,

ⓘ

Symbols:

${𝐇}_{\nu }\left(z\right)$: Struve function, $\pi$: the ratio of the circumference of a circle to its diameter, $\cot z$: cotangent function, $dx$: differential of $x$ , $\int$: integral, $\mathrm{\Re }$: real part and $\nu$: real or complex order

Permalink:

http://dlmf.nist.gov/11.7.E9

Encodings:

pMML, png, TeX

See also:

Annotations for §11.7(ii), §11.7 and Ch.11

►

11.7.10 $${\int }_0^{\mathrm{\infty }}{t}^{-\nu -1}{𝐇}_{\nu }\left(t\right)dt=\frac{\pi }{2^{\nu +1}\mathrm{\Gamma }\left(\nu +1\right)},$$ $\mathrm{\Re }\nu >-\frac{3}{2}$,

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, ${𝐇}_{\nu }\left(z\right)$: Struve function, $\pi$: the ratio of the circumference of a circle to its diameter, $dx$: differential of $x$ , $\int$: integral, $\mathrm{\Re }$: real part and $\nu$: real or complex order

Keywords:

Mellin transform

Permalink:

http://dlmf.nist.gov/11.7.E10

Encodings:

pMML, png, TeX

See also:

Annotations for §11.7(ii), §11.7 and Ch.11

►

11.7.11 $${\int }_0^{\mathrm{\infty }}{t}^{\mu -\nu -1}{𝐇}_{\nu }\left(t\right)dt=\frac{\mathrm{\Gamma }\left(\frac{1}{2}\mu \right)2^{\mu -\nu -1}\tan \left(\frac{1}{2}\pi \mu \right)}{\mathrm{\Gamma }\left(\nu -\frac{1}{2}\mu +1\right)},$$ , $\mathrm{\Re }\nu >\mathrm{\Re }\mu -\frac{3}{2}$,

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, ${𝐇}_{\nu }\left(z\right)$: Struve function, $\pi$: the ratio of the circumference of a circle to its diameter, $dx$: differential of $x$ , $\int$: integral, $\mathrm{\Re }$: real part, $\tan z$: tangent function and $\nu$: real or complex order

Keywords:

Mellin transform

A&S Ref:

12.1.27

Permalink:

http://dlmf.nist.gov/11.7.E11

Encodings:

pMML, png, TeX

See also:

Annotations for §11.7(ii), §11.7 and Ch.11

… ►The following Laplace transforms of ${𝐇}_{\nu }\left(t\right)$ require $\mathrm{\Re }a>0$ for convergence, while those of ${𝐋}_{\nu }\left(t\right)$ require $\mathrm{\Re }a>1$. …

26: 35.3 Multivariate Gamma and Beta Functions

… ►

35.3.1 $${\mathrm{\Gamma }}_m\left(a\right)={\int }_{𝛀}\mathrm{etr}\left(-𝐗\right){\left|𝐗\right|}^{a-\frac{1}{2}(m+1)}d𝐗,$$ $\mathrm{\Re }\left(a\right)>\frac{1}{2}(m-1)$.

ⓘ

Symbols:

$\mathrm{etr}\left(𝐀\right)$: exponential of trace, $\int$: integral, ${\mathrm{\Gamma }}_m\left(a\right)$: multivariate gamma function, $\mathrm{\Re }$: real part, $a$: complex variable, $𝐗$: real symmetric $m\times m$ matrix, $\left|𝐗\right|$: determinant of $𝐗$ , $d$: differential of matrix, $𝛀$: space of positive-definite real symmetric $m\times m$ matrices and $m$: positive integer

Permalink:

http://dlmf.nist.gov/35.3.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §35.3(i), §35.3 and Ch.35

►

35.3.2 $${\mathrm{\Gamma }}_m\left(s_1,\mathrm{\dots },s_m\right)={\int }_{𝛀}\mathrm{etr}\left(-𝐗\right){\left|𝐗\right|}^{s_m-\frac{1}{2}(m+1)}\prod _{j=1}^{m-1}{|{(𝐗)}_j|}^{s_j-s_{j+1}}d𝐗,$$ $s_j\in ℂ$, $\mathrm{\Re }\left(s_j\right)>\frac{1}{2}(j-1)$, $j=1,\mathrm{\dots },m$.

ⓘ

Symbols:

$ℂ$: complex plane, $\in$: element of, $\mathrm{etr}\left(𝐀\right)$: exponential of trace, $\int$: integral, ${\mathrm{\Gamma }}_m\left(a\right)$: multivariate gamma function, $\mathrm{\Re }$: real part, $𝐗$: real symmetric $m\times m$ matrix, $\left|𝐗\right|$: determinant of $𝐗$ , $|{(𝐗)}_j|$: $j$th principal minor of $𝐗$ , $d$: differential of matrix, $𝛀$: space of positive-definite real symmetric $m\times m$ matrices, $j$: nonnegative integer and $m$: positive integer

Permalink:

http://dlmf.nist.gov/35.3.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §35.3(i), §35.3 and Ch.35

►

35.3.3 $\mathrm{\Re }\left(a\right),\mathrm{\Re }\left(b\right)>\frac{1}{2}(m-1)$.

ⓘ

Defines:

${\mathrm{B}}_m(a,b)$: multivariate beta function

Symbols:

$\int$: integral, $\mathrm{\Re }$: real part, $a$: complex variable, $𝐈$: $m\times m$ identity matrix, $𝐗$: real symmetric $m\times m$ matrix, $\left|𝐗\right|$: determinant of $𝐗$ , $d$: differential of matrix, $b$: complex variable, : less-than for matrices, $m$: positive integer and $𝟎$: $m\times m$ matrix of zeros

Keywords:

definition, multivariate beta function

Permalink:

http://dlmf.nist.gov/35.3.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §35.3(i), §35.3 and Ch.35

… ►

35.3.8 $${\mathrm{B}}_m(a,b)={\int }_{𝛀}{\left|𝐗\right|}^{a-\frac{1}{2}(m+1)}{\left|𝐈+𝐗\right|}^{-(a+b)}d𝐗,$$ $\mathrm{\Re }\left(a\right),\mathrm{\Re }\left(b\right)>\frac{1}{2}(m-1)$.

ⓘ

Symbols:

$\int$: integral, ${\mathrm{B}}_m(a,b)$: multivariate beta function, $\mathrm{\Re }$: real part, $a$: complex variable, $𝐈$: $m\times m$ identity matrix, $𝐗$: real symmetric $m\times m$ matrix, $\left|𝐗\right|$: determinant of $𝐗$ , $d$: differential of matrix, $𝛀$: space of positive-definite real symmetric $m\times m$ matrices, $b$: complex variable and $m$: positive integer

Permalink:

http://dlmf.nist.gov/35.3.E8

Encodings:

pMML, png, TeX

See also:

Annotations for §35.3(ii), §35.3 and Ch.35

27: 8.22 Mathematical Applications

… ►The function $\mathrm{\Gamma }(a,z)$, with $|\mathrm{ph}a|\le \frac{1}{2}\pi$ and $\mathrm{ph}z=\frac{1}{2}\pi$, has an intimate connection with the Riemann zeta function $\zeta \left(s\right)$ (§25.2(i)) on the critical line $\mathrm{\Re }s=\frac{1}{2}$. … ►

8.22.2 $${\zeta }_x(s)=\frac{1}{\mathrm{\Gamma }\left(s\right)}{\int }_0^x\frac{t^{s-1}}{{\mathrm{e}}^t-1}dt,$$ $\mathrm{\Re }s>1$,

ⓘ

Defines:

${\zeta }_x(s)$: incomplete Riemann zeta function (locally)

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $dx$: differential of $x$ , $\mathrm{e}$: base of natural logarithm, $\int$: integral, $\mathrm{\Re }$: real part and $x$: real variable

Permalink:

http://dlmf.nist.gov/8.22.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §8.22(ii), §8.22 and Ch.8

… ►

8.22.3 $${\zeta }_x(s)=\sum _{k=1}^{\mathrm{\infty }}{k}^{-s}P(s,kx),$$ $\mathrm{\Re }s>1$.

ⓘ

Symbols:

$P(a,z)$: normalized incomplete gamma function, $\mathrm{\Re }$: real part, $x$: real variable, $k$: nonnegative integer and ${\zeta }_x(s)$: incomplete Riemann zeta function

Permalink:

http://dlmf.nist.gov/8.22.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §8.22(ii), §8.22 and Ch.8

…

28: 25.11 Hurwitz Zeta Function

… ►As a function of $a$, with $s$ ($\ne 1$) fixed, $\zeta (s,a)$ is analytic in the half-plane $\mathrm{\Re }a>0$. … ►For most purposes it suffices to restrict because of the following straightforward consequences of (25.11.1): … ►

25.11.9 $$\zeta (1-s,a)=\frac{2\mathrm{\Gamma }\left(s\right)}{{(2\pi )}^s}\sum _{n=1}^{\mathrm{\infty }}\frac{1}{n^s}\cos \left(\frac{1}{2}\pi s-2n\pi a\right),$$ $\mathrm{\Re }s>0$ if ; $\mathrm{\Re }s>1$ if $a=1$.

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $\zeta (s,a)$: Hurwitz zeta function, $\pi$: the ratio of the circumference of a circle to its diameter, $\cos z$: cosine function, $\mathrm{\Re }$: real part, $n$: nonnegative integer, $a$: real or complex parameter and $s$: complex variable

Keywords:

infinite series, series representation

Source:

Apostol (1976, (9), (10), p. 257)

Referenced by:

(25.13.3), Erratum (V1.1.4) for Equation (25.11.9)

Permalink:

http://dlmf.nist.gov/25.11.E9

Encodings:

pMML, png, TeX

Clarification (effective with 1.1.4):

The constraint which originally read “$\mathrm{\Re }s>1$, ” has been extended to be “$\mathrm{\Re }s>0$ if ; $\mathrm{\Re }s>1$ if $a=1$”.

Suggested 2021-08-23 by Gergő Nemes

See also:

Annotations for §25.11(iv), §25.11 and Ch.25

… ►Throughout this subsection $\mathrm{\Re }a>0$. … ►As $\beta \to \pm \mathrm{\infty }$ with $s$ fixed, $\mathrm{\Re }s>1$, …

29: 10.43 Integrals

… ►when $\mathrm{\Re }\alpha >0$ and $x>0$, and by analytic continuation elsewhere. … ►When $\mathrm{\Re }\mu >|\mathrm{\Re }\nu |$, … ►

10.43.23 $${\int }_0^{\mathrm{\infty }}{t}^{\nu +1}{I}_{\nu }\left(bt\right)\exp \left(-p^2{t}^2\right)dt=\frac{b^{\nu }}{{(2p^2)}^{\nu +1}}\exp \left(\frac{b^2}{4p^2}\right),$$ $\mathrm{\Re }\nu >-1,\mathrm{\Re }\left(p^2\right)>0$,

ⓘ

Symbols:

$dx$: differential of $x$ , $\exp z$: exponential function, $\int$: integral, $I_{\nu }\left(z\right)$: modified Bessel function of the first kind, $\mathrm{\Re }$: real part and $\nu$: complex parameter

Keywords:

Mellin transform

Referenced by:

§10.43(iv)

Permalink:

http://dlmf.nist.gov/10.43.E23

Encodings:

pMML, png, TeX

See also:

Annotations for §10.43(iv), §10.43 and Ch.10

►

10.43.24 $${\int }_0^{\mathrm{\infty }}{I}_{\nu }\left(bt\right)\exp \left(-p^2{t}^2\right)dt=\frac{\sqrt{\pi }}{2p}\exp \left(\frac{b^2}{8p^2}\right)I_{\frac{1}{2}\nu }\left(\frac{b^2}{8p^2}\right),$$ $\mathrm{\Re }\nu >-1$, $\mathrm{\Re }\left(p^2\right)>0$,

ⓘ

Symbols:

$\pi$: the ratio of the circumference of a circle to its diameter, $dx$: differential of $x$ , $\exp z$: exponential function, $\int$: integral, $I_{\nu }\left(z\right)$: modified Bessel function of the first kind, $\mathrm{\Re }$: real part and $\nu$: complex parameter

A&S Ref:

11.4.31

Permalink:

http://dlmf.nist.gov/10.43.E24

Encodings:

pMML, png, TeX

See also:

Annotations for §10.43(iv), §10.43 and Ch.10

… ►

10.43.28 $${\int }_0^{\mathrm{\infty }}t\exp \left(-p^2{t}^2\right)I_{\nu }\left(at\right)I_{\nu }\left(bt\right)dt=\frac{1}{2p^2}\exp \left(\frac{a^2+b^2}{4p^2}\right)I_{\nu }\left(\frac{ab}{2p^2}\right),$$ $\mathrm{\Re }\nu >-1,\mathrm{\Re }\left(p^2\right)>0$,

ⓘ

Symbols:

$dx$: differential of $x$ , $\exp z$: exponential function, $\int$: integral, $I_{\nu }\left(z\right)$: modified Bessel function of the first kind, $\mathrm{\Re }$: real part and $\nu$: complex parameter

Permalink:

http://dlmf.nist.gov/10.43.E28

Encodings:

pMML, png, TeX

See also:

Annotations for §10.43(iv), §10.43 and Ch.10

…

30: 4.24 Inverse Trigonometric Functions: Further Properties

… ►

4.24.4 $$\arctan z=\pm \frac{\pi }{2}-\frac{1}{z}+\frac{1}{3z^3}-\frac{1}{5z^5}+\mathrm{\cdots },$$ $\mathrm{\Re }z\gtrless 0$, $|z|\ge 1$.

ⓘ

Symbols:

$\pi$: the ratio of the circumference of a circle to its diameter, $\arctan z$: arctangent function, $\mathrm{\Re }$: real part and $z$: complex variable

A&S Ref:

4.4.42 (has an error. $\frac{\pi }{2}$ should have a negative sign when .)

Referenced by:

§4.45(i)

Permalink:

http://dlmf.nist.gov/4.24.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §4.24(i), §4.24 and Ch.4

►

4.24.5 $$\arctan z=\frac{z}{z^2+1}\left(1+\frac{2}{3}\frac{z^2}{1+z^2}+\frac{2\cdot 4}{3\cdot 5}{\left(\frac{z^2}{1+z^2}\right)}^2+\mathrm{\cdots }\right),$$ $\mathrm{\Re }\left(z^2\right)>-\frac{1}{2}$,

ⓘ

Symbols:

$\arctan z$: arctangent function, $\mathrm{\Re }$: real part and $z$: complex variable

A&S Ref:

4.4.42 (has an error in the conditions on $z$.)

Permalink:

http://dlmf.nist.gov/4.24.E5

Encodings:

pMML, png, TeX

See also:

Annotations for §4.24(i), §4.24 and Ch.4

… ►

4.24.10 $$\frac{d}{dz}\mathrm{arccsc}z=\mp \frac{1}{z{(z^2-1)}^{1/2}},$$ $\mathrm{\Re }z\gtrless 0$.

ⓘ

Symbols:

$\frac{df}{dx}$: derivative of $f$ with respect to $x$ , $\mathrm{arccsc}z$: arccosecant function, $\mathrm{\Re }$: real part and $z$: complex variable

A&S Ref:

4.4.57 (has an error.)

Referenced by:

§4.24(ii)

Permalink:

http://dlmf.nist.gov/4.24.E10

Encodings:

pMML, png, TeX

See also:

Annotations for §4.24(ii), §4.24 and Ch.4

►

4.24.11 $$\frac{d}{dz}\mathrm{arcsec}z=\pm \frac{1}{z{(z^2-1)}^{1/2}},$$ $\mathrm{\Re }z\gtrless 0$.

ⓘ

Symbols:

$\frac{df}{dx}$: derivative of $f$ with respect to $x$ , $\mathrm{arcsec}z$: arcsecant function, $\mathrm{\Re }$: real part and $z$: complex variable

A&S Ref:

4.4.56 (has an error.)

Referenced by:

§4.24(ii)

Permalink:

http://dlmf.nist.gov/4.24.E11

Encodings:

pMML, png, TeX

See also:

Annotations for §4.24(ii), §4.24 and Ch.4

…