19 Elliptic Integrals Legendre’s Integrals 19.2 Definitions 19.4 Derivatives and Differential Equations

§19.3 Graphics

Keywords:: Legendre’s elliptic integrals
Permalink:: http://dlmf.nist.gov/19.3

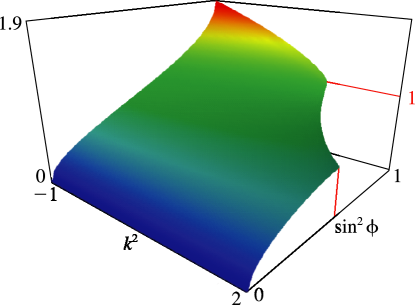
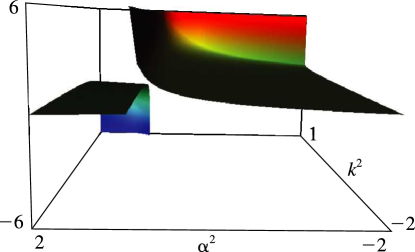
§19.3(i) Real Variables
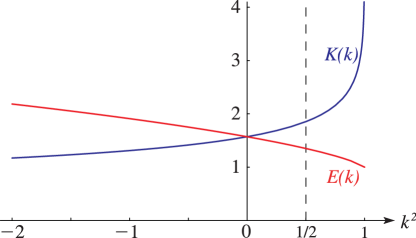
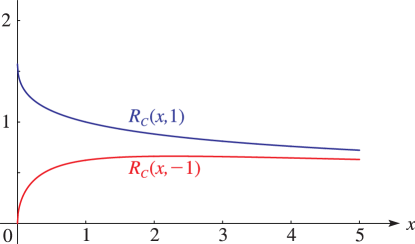
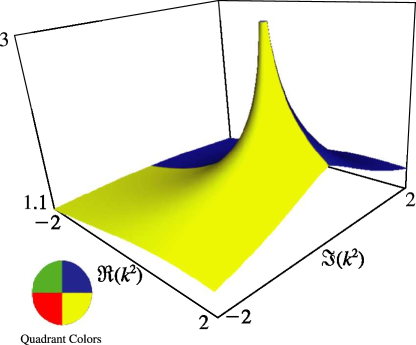
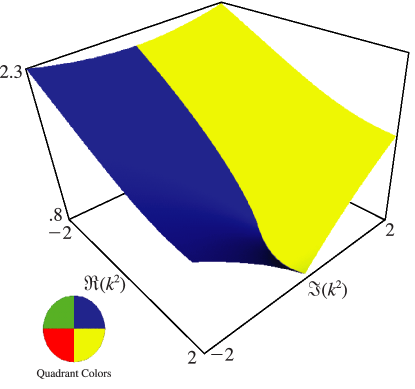
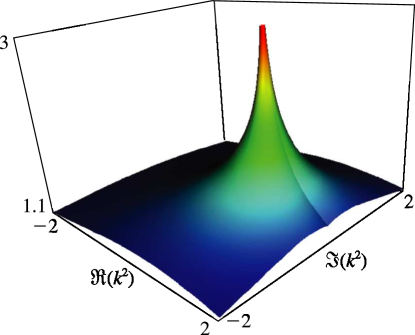
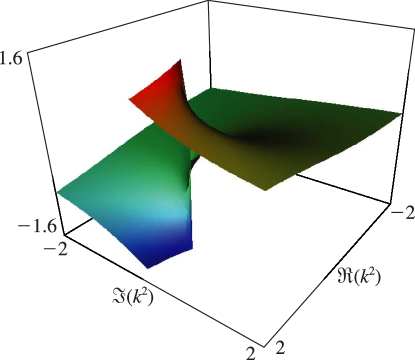
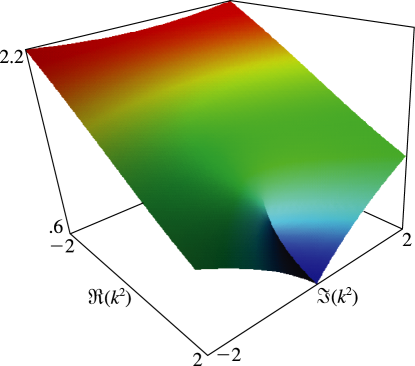
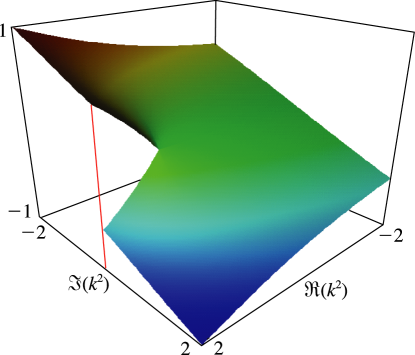
§19.3(ii) Complex Variables

§19.3(i) Real Variables

Notes:: These graphics were produced at NIST.
Permalink:: http://dlmf.nist.gov/19.3.i

See Figures 19.3.1–19.3.6 for complete and incomplete Legendre’s elliptic integrals.

Figure 19.3.1: $\mathop{K\/}\nolimits\!\left(k\right)$ and $\mathop{E\/}\nolimits\!\left(k\right)$ as functions of $k^{2}$ for $-2\leq k^{2}\leq 1$ . Graphs of $\mathop{{K^{{\prime}}}\/}\nolimits\!\left(k\right)$ and $\mathop{{E^{{\prime}}}\/}\nolimits\!\left(k\right)$ are the mirror images in the vertical line $k^{2}=\frac{1}{2}$ .

Symbols:: $\mathop{{K^{{\prime}}}\/}\nolimits\!\left(k\right)$ : Legendre’s complementary complete elliptic integral of the first kind, $\mathop{{E^{{\prime}}}\/}\nolimits\!\left(k\right)$ : Legendre’s complementary complete elliptic integral of the second kind, $\mathop{K\/}\nolimits\!\left(k\right)$ : Legendre’s complete elliptic integral of the first kind, $\mathop{E\/}\nolimits\!\left(k\right)$ : Legendre’s complete elliptic integral of the second kind and : real or complex modulus
Referenced by:: §19.3(i)
Permalink:: http://dlmf.nist.gov/19.3.F1
Encodings:: pdf, png

Figure 19.3.2: $\mathop{R_{C}\/}\nolimits\!\left(x,1\right)$ and the Cauchy principal value of $\mathop{R_{C}\/}\nolimits\!\left(x,-1\right)$ for $0\leq x\leq 5$ . Both functions are asymptotic to $\mathop{\ln\/}\nolimits\!\left(4x\right)/\sqrt{4x}$ as $x\to\infty$ ; see (19.2.19) and (19.2.20). Note that $\mathop{R_{C}\/}\nolimits\!\left(x,\pm y\right)=y^{{-1/2}}\mathop{R_{C}\/}% \nolimits\!\left(x/y,\pm 1\right)$ ,

Symbols:: $\mathop{R_{C}\/}\nolimits\!\left(x,y\right)$ : Carlson’s combination of inverse circular and inverse hyperbolic functions and $\mathop{\ln\/}\nolimits z$ : principal branch of logarithm function
Referenced by:: §19.17
Permalink:: http://dlmf.nist.gov/19.3.F2
Encodings:: pdf, png

Visualization Help

Figure 19.3.3: $\mathop{F\/}\nolimits\!\left(\phi,k\right)$ as a function of $k^{2}$ and ${\mathop{\sin\/}\nolimits^{{2}}}\phi$ for $-1\leq k^{2}\leq 2$ , $0\leq{\mathop{\sin\/}\nolimits^{{2}}}\phi\leq 1$ . If ${\mathop{\sin\/}\nolimits^{{2}}}\phi=1$ ( $\geq k^{2}$ ), then the function reduces to $\mathop{K\/}\nolimits\!\left(k\right)$ , becoming infinite when $k^{2}=1$ . If ${\mathop{\sin\/}\nolimits^{{2}}}\phi=1/k^{2}$ (

), then it has the value $\mathop{K\/}\nolimits\!\left(1/k\right)/k$ : put $c=k^{2}$ in (19.25.5) and use (19.25.1).

Symbols:: $\mathop{K\/}\nolimits\!\left(k\right)$ : Legendre’s complete elliptic integral of the first kind, $\mathop{F\/}\nolimits\!\left(\phi,k\right)$ : Legendre’s incomplete elliptic integral of the first kind, $\mathop{\sin\/}\nolimits z$ : sine function, $\phi$ : real or complex argument and : real or complex modulus
Permalink:: http://dlmf.nist.gov/19.3.F3
Encodings:: VRML, X3D, pdf, png

Visualization Help

Figure 19.3.4: $\mathop{E\/}\nolimits\!\left(\phi,k\right)$ as a function of $k^{2}$ and ${\mathop{\sin\/}\nolimits^{{2}}}\phi$ for $-1\leq k^{2}\leq 2$ , $0\leq{\mathop{\sin\/}\nolimits^{{2}}}\phi\leq 1$ . If ${\mathop{\sin\/}\nolimits^{{2}}}\phi=1$ ( $\geq k^{2}$ ), then the function reduces to $\mathop{E\/}\nolimits\!\left(k\right)$ , with value 1 at $k^{2}=1$ . If ${\mathop{\sin\/}\nolimits^{{2}}}\phi=1/k^{2}$ (

), then it has the value $k\mathop{E\/}\nolimits\!\left(1/k\right)+({k^{{\prime}}}^{2}/k)\mathop{K\/}% \nolimits\!\left(1/k\right)$ , with limit 1 as $k^{2}\to 1+$ : put $c=k^{2}$ in (19.25.7) and use (19.25.1).

Symbols:: $\mathop{K\/}\nolimits\!\left(k\right)$ : Legendre’s complete elliptic integral of the first kind, $\mathop{E\/}\nolimits\!\left(k\right)$ : Legendre’s complete elliptic integral of the second kind, $\mathop{E\/}\nolimits\!\left(\phi,k\right)$ : Legendre’s incomplete elliptic integral of the second kind, $\mathop{\sin\/}\nolimits z$ : sine function, $\phi$ : real or complex argument, : real or complex modulus and $k^{{\prime}}$ : complementary modulus
Permalink:: http://dlmf.nist.gov/19.3.F4
Encodings:: VRML, X3D, pdf, png

Visualization Help

Figure 19.3.5: $\mathop{\Pi\/}\nolimits\!\left(\alpha^{2},k\right)$ as a function of $k^{2}$ and $\alpha^{2}$ for $-2\leq k^{2}<1$ , $-2\leq\alpha^{2}\leq 2$ . Cauchy principal values are shown when $\alpha^{2}>1$ . The function is unbounded as $\alpha^{2}\to 1-$ , and also (with the same sign as $1-\alpha^{2}$ ) as $k^{2}\to 1-$ . As $\alpha^{2}\to 1+$ it has the limit $\mathop{K\/}\nolimits\!\left(k\right)-(\mathop{E\/}\nolimits\!\left(k\right)/{% k^{{\prime}}}^{2})$ . If $\alpha^{2}=0$ , then it reduces to $\mathop{K\/}\nolimits\!\left(k\right)$ . If $k^{2}=0$ , then it has the value $\frac{1}{2}\pi/\sqrt{1-\alpha^{2}}$ when $\alpha^{2}<1$ , and 0 when $\alpha^{2}>1$ . See §19.6(i).

Symbols:: $\mathop{K\/}\nolimits\!\left(k\right)$ : Legendre’s complete elliptic integral of the first kind, $\mathop{E\/}\nolimits\!\left(k\right)$ : Legendre’s complete elliptic integral of the second kind, $\mathop{\Pi\/}\nolimits\!\left(\alpha^{2},k\right)$ : Legendre’s complete elliptic integral of the third kind, : real or complex modulus, $k^{{\prime}}$ : complementary modulus and $\alpha^{2}$ : real or complex parameter
Permalink:: http://dlmf.nist.gov/19.3.F5
Encodings:: VRML, X3D, pdf, png

Visualization Help

Figure 19.3.6: $\mathop{\Pi\/}\nolimits\!\left(\phi,2,k\right)$ as a function of $k^{2}$ and ${\mathop{\sin\/}\nolimits^{{2}}}\phi$ for $-1\leq k^{2}\leq 3$ , $0\leq{\mathop{\sin\/}\nolimits^{{2}}}\phi<1$ . Cauchy principal values are shown when ${\mathop{\sin\/}\nolimits^{{2}}}\phi>\frac{1}{2}$ . The function tends to $+\infty$ as ${\mathop{\sin\/}\nolimits^{{2}}}\phi\to\frac{1}{2}$ , except in the last case below. If ${\mathop{\sin\/}\nolimits^{{2}}}\phi=1$ ( $>k^{2}$ ), then the function reduces to $\mathop{\Pi\/}\nolimits\!\left(2,k\right)$ with Cauchy principal value $\mathop{K\/}\nolimits\!\left(k\right)-\mathop{\Pi\/}\nolimits\!\left(\frac{1}{% 2}k^{2},k\right)$ , which tends to $-\infty$ as $k^{2}\to 1-$ . See (19.6.5) and (19.6.6). If ${\mathop{\sin\/}\nolimits^{{2}}}\phi=1/k^{2}$ (

), then by (19.7.4) it reduces to $\mathop{\Pi\/}\nolimits\!\left(2/k^{2},1/k\right)/k$ , $k^{2}\neq 2$ , with Cauchy principal value $(\mathop{K\/}\nolimits\!\left(1/k\right)-\mathop{\Pi\/}\nolimits\!\left(\frac{% 1}{2},1/k\right))/k$ , $1<k^{2}<2$ , by (19.6.5). Its value tends to $-\infty$ as $k^{2}\to 1+$ by (19.6.6), and to the negative of the second lemniscate constant (see (19.20.22)) as $k^{2}(={\mathop{\csc\/}\nolimits^{{2}}}\phi)\to 2-$ .

Symbols:: $\mathop{K\/}\nolimits\!\left(k\right)$ : Legendre’s complete elliptic integral of the first kind, $\mathop{\Pi\/}\nolimits\!\left(\alpha^{2},k\right)$ : Legendre’s complete elliptic integral of the third kind, $\mathop{\csc\/}\nolimits z$ : cosecant function, $\mathop{\Pi\/}\nolimits\!\left(\phi,\alpha^{2},k\right)$ : Legendre’s incomplete elliptic integral of the third kind, $\mathop{\sin\/}\nolimits z$ : sine function, $\phi$ : real or complex argument and : real or complex modulus
Referenced by:: §19.3(i)
Permalink:: http://dlmf.nist.gov/19.3.F6
Encodings:: VRML, X3D, pdf, png

§19.3(ii) Complex Variables

Notes:: These graphics were produced at NIST.
Keywords:: Legendre’s elliptic integrals
Permalink:: http://dlmf.nist.gov/19.3.ii

In Figures 19.3.7 and 19.3.8 for complete Legendre’s elliptic integrals with complex arguments, height corresponds to the absolute value of the function and color to the phase. See also About Color Map.

Visualization Help

Figure 19.3.7: $\mathop{K\/}\nolimits\!\left(k\right)$ as a function of complex $k^{2}$ for $-2\leq\realpart{(k^{2})}\leq 2$ , $-2\leq\imagpart{(k^{2})}\leq 2$ . There is a branch cut where $1<k^{2}<\infty$ .

Symbols:: $\mathop{K\/}\nolimits\!\left(k\right)$ : Legendre’s complete elliptic integral of the first kind, $\imagpart{}$ : imaginary part, $\realpart{}$ : real part and : real or complex modulus
Referenced by:: §19.17, §19.17, §19.3(ii)
Permalink:: http://dlmf.nist.gov/19.3.F7
Encodings:: VRML, X3D, pdf, png

Visualization Help

Figure 19.3.8: $\mathop{E\/}\nolimits\!\left(k\right)$ as a function of complex $k^{2}$ for $-2\leq\realpart{(k^{2})}\leq 2$ , $-2\leq\imagpart{(k^{2})}\leq 2$ . There is a branch cut where $1<k^{2}<\infty$ .

Symbols:: $\mathop{E\/}\nolimits\!\left(k\right)$ : Legendre’s complete elliptic integral of the second kind, $\imagpart{}$ : imaginary part, $\realpart{}$ : real part and : real or complex modulus
Referenced by:: §19.3(ii)
Permalink:: http://dlmf.nist.gov/19.3.F8
Encodings:: VRML, X3D, pdf, png

Visualization Help

Figure 19.3.9: $\realpart{(\mathop{K\/}\nolimits\!\left(k\right))}$ as a function of complex $k^{2}$ for $-2\leq\realpart{(k^{2})}\leq 2$ , $-2\leq\imagpart{(k^{2})}\leq 2$ . The real part is symmetric under reflection in the real axis. On the branch cut ( $k^{2}\geq 1$ ) it is infinite at $k^{2}=1$ , and has the value $\mathop{K\/}\nolimits(1/k)/k$ when $k^{2}>1$ .

Symbols:: $\mathop{K\/}\nolimits\!\left(k\right)$ : Legendre’s complete elliptic integral of the first kind, $\imagpart{}$ : imaginary part, $\realpart{}$ : real part and : real or complex modulus
Permalink:: http://dlmf.nist.gov/19.3.F9
Encodings:: VRML, X3D, pdf, png

Visualization Help

Figure 19.3.10: $\imagpart{(\mathop{K\/}\nolimits\!\left(k\right))}$ as a function of complex $k^{2}$ for $-2\leq\realpart{(k^{2})}\leq 2$ , $-2\leq\imagpart{(k^{2})}\leq 2$ . The imaginary part is 0 for $k^{2}<1$ , and is antisymmetric under reflection in the real axis. On the upper edge of the branch cut ( $k^{2}\geq 1$ ) it has the value $\mathop{K\/}\nolimits\!\left(k^{{\prime}}\right)$ if $k^{2}>1$ , and $\frac{1}{4}\pi$ if $k^{2}=1$ .

Symbols:: $\mathop{K\/}\nolimits\!\left(k\right)$ : Legendre’s complete elliptic integral of the first kind, $\imagpart{}$ : imaginary part, $\realpart{}$ : real part, : real or complex modulus and $k^{{\prime}}$ : complementary modulus
Permalink:: http://dlmf.nist.gov/19.3.F10
Encodings:: VRML, X3D, pdf, png

Visualization Help

Figure 19.3.11: $\realpart{(\mathop{E\/}\nolimits\!\left(k\right))}$ as a function of complex $k^{2}$ for $-2\leq\realpart{(k^{2})}\leq 2$ , $-2\leq\imagpart{(k^{2})}\leq 2$ . The real part is symmetric under reflection in the real axis. On the branch cut ( $k^{2}>1$ ) it has the value $k\mathop{E\/}\nolimits\!\left(1/k\right)+({k^{{\prime}}}^{2}/k)\mathop{K\/}% \nolimits\!\left(1/k\right)$ , with limit 1 as $k^{2}\to 1+$ .

Symbols:: $\mathop{K\/}\nolimits\!\left(k\right)$ : Legendre’s complete elliptic integral of the first kind, $\mathop{E\/}\nolimits\!\left(k\right)$ : Legendre’s complete elliptic integral of the second kind, $\imagpart{}$ : imaginary part, $\realpart{}$ : real part, : real or complex modulus and $k^{{\prime}}$ : complementary modulus
Permalink:: http://dlmf.nist.gov/19.3.F11
Encodings:: VRML, X3D, pdf, png

Visualization Help

Figure 19.3.12: $\imagpart{(\mathop{E\/}\nolimits\!\left(k\right))}$ as a function of complex $k^{2}$ for $-2\leq\realpart{(k^{2})}\leq 2$ , $-2\leq\imagpart{(k^{2})}\leq 2$ . The imaginary part is 0 for $k^{2}\leq 1$ and is antisymmetric under reflection in the real axis. On the upper edge of the branch cut ( $k^{2}>1$ ) it has the (negative) value $\mathop{K\/}\nolimits\!\left(k^{{\prime}}\right)-\mathop{E\/}\nolimits\!\left(% k^{{\prime}}\right)$ , with limit 0 as $k^{2}\to 1+$ .

Symbols:: $\mathop{K\/}\nolimits\!\left(k\right)$ : Legendre’s complete elliptic integral of the first kind, $\mathop{E\/}\nolimits\!\left(k\right)$ : Legendre’s complete elliptic integral of the second kind, $\imagpart{}$ : imaginary part, $\realpart{}$ : real part, : real or complex modulus and $k^{{\prime}}$ : complementary modulus
Referenced by:: §19.17, §19.17
Permalink:: http://dlmf.nist.gov/19.3.F12
Encodings:: VRML, X3D, pdf, png

© 2010–2013 NIST / Privacy Policy / Disclaimer / Feedback; Version 1.0.6; Release date 2013-05-06 Math-Image version (See MathML) . A Printed Companionis available. 19.2 Definitions 19.4 Derivatives and Differential Equations

§19.3 Graphics

Contents

§19.3(i) Real Variables

§19.3(ii) Complex Variables