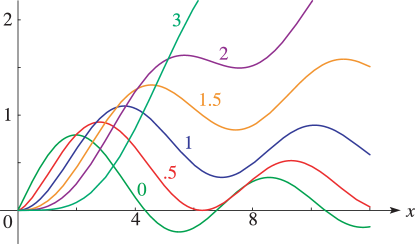
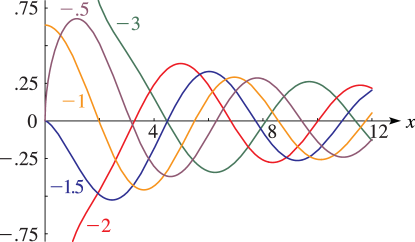
orders ±12

SearchAdvancedHelp

(0.002 seconds)

11—20 of 67 matching pages

11: Nico M. Temme

… ►On the occasion of his retirement in 2005 he was awarded the decoration Knight in the Order of the Dutch Lion, issued by the King of the Netherlands. … ►

12 Parabolic Cylinder Functions

… ►In November 2015, Temme was named Senior Associate Editor of the DLMF and Associate Editor for Chapters 3, 6, 7, and 12.

12: Bibliography O

… ►

Hyperasymptotic solutions of second-order linear differential equations. I. Methods Appl. Anal. 2 (2), pp. 173–197.

ⓘ

External Links:

ISSN 1073-2772, FullText, MathReview (A. D. Wood), ZentralBlatt

Referenced by:

§10.17(v), §10.40(iv), §13.29(i), §13.7(iii), §2.11(v), §9.7(v).

Encodings:

BibTeX

►

On the calculation of Stokes multipliers for linear differential equations of the second order. Methods Appl. Anal. 2 (3), pp. 348–367.

ⓘ

External Links:

ISSN 1073-2772, Pdf, MathReview (Archibald D. MacGillivray), ZentralBlatt

Referenced by:

§2.7(ii).

Encodings:

BibTeX

… ►

Hyperasymptotic solutions of second-order linear differential equations. II. Methods Appl. Anal. 2 (2), pp. 198–211.

ⓘ

External Links:

ISSN 1073-2772, FullText, MathReview (A. D. Wood), ZentralBlatt

Referenced by:

§10.17(v), §10.40(iv), §2.11(v), §9.7(v).

Encodings:

BibTeX

… ►

Error bounds for asymptotic expansions in turning-point problems. J. Soc. Indust. Appl. Math. 12 (1), pp. 200–214.

ⓘ

External Links:

Document, MathReview (N. D. Kazarinoff), ZentralBlatt

Referenced by:

§2.8(iii).

Encodings:

BibTeX

… ►

Second-order differential equations with fractional transition points. Trans. Amer. Math. Soc. 226, pp. 227–241.

ⓘ

External Links:

FullText, MathReview (Anthony Leung), ZentralBlatt

Referenced by:

§2.8(v).

Encodings:

BibTeX

…

13: 11.3 Graphics

… ►

►►

Figure 11.3.1: ${𝐇}_{\nu }\left(x\right)$ for $0\le x\le 12$ and $\nu =0,\frac{1}{2},1,\frac{3}{2},2,3$. Magnify

… ►

►►

Figure 11.3.3: ${𝐇}_{\nu }\left(x\right)$ for $0\le x\le 12$ and $\nu =-3,-2,-\frac{3}{2},-1,-\frac{1}{2}$. Magnify

…

14: 14.26 Uniform Asymptotic Expansions

§14.26 Uniform Asymptotic Expansions

►The uniform asymptotic approximations given in §14.15 for $P_{\nu }^{-\mu }\left(x\right)$ and ${𝑸}_{\nu }^{\mu }\left(x\right)$ for are extended to domains in the complex plane in the following references: §§14.15(i) and 14.15(ii), Dunster (2003b); §14.15(iii), Olver (1997b, Chapter 12); §14.15(iv), Boyd and Dunster (1986). …

15: Bibliography M

… ►

Algorithm 779: Fermi-Dirac functions of order $-1/2$, $1/2$, $3/2$, $5/2$ . ACM Trans. Math. Software 24 (1), pp. 1–12.

ⓘ

Notes:

Double-precision Fortran, maximum accuracy 16D.

External Links:

ISSN 0098-3500, Document, GAMS (module 779; package TOMS), ZentralBlatt

Referenced by:

8th item.

Encodings:

BibTeX

…

16: 13.8 Asymptotic Approximations for Large Parameters

… ►

13.8.17 $$M(a,b,z)={\mathrm{e}}^{\nu z}\frac{{\mathrm{\Gamma }}^{\ast }(b)}{{\mathrm{\Gamma }}^{\ast }(a)}\left(1+\frac{(1-\nu )(1+6{\nu }^2{z}^2)}{12a}+O\left(\frac{1}{\min (a^2,b^2)}\right)\right),$$

ⓘ

Symbols:

$O\left(x\right)$: order not exceeding, $M(a,b,z)$: $={}_1{}^{}F_1^{}(a;b;z)$ Kummer confluent hypergeometric function, $\mathrm{e}$: base of natural logarithm and $z$: complex variable

Permalink:

http://dlmf.nist.gov/13.8.E17

Encodings:

pMML, png, TeX

See also:

Annotations for §13.8(iv), §13.8 and Ch.13

…

17: Bibliography G

… ►

Algorithm 471: Exponential integrals. Comm. ACM 16 (12), pp. 761–763.

ⓘ

Notes:

Includes Algol60 program, maximum accuracy 10S.

External Links:

ISSN 0001-0782, Document

Referenced by:

§6.21(ii), §8.28(vi).

Encodings:

BibTeX

… ►

Mémoire sur les fonctions hypergéométriques d’ordre supérieur. Ann. Sci. École Norm. Sup. (2) 12, pp. 261–286, 395–430 (French).

ⓘ

External Links:

ZentralBlatt

Referenced by:

§16.12.

Encodings:

BibTeX

… ►

The solutions of Painlevé’s fifth equation. Differ. Uravn. 12 (4), pp. 740–742 (Russian).

ⓘ

Notes:

In Russian. English translation: Differential Equations 12(4), pp. 519–521 (1977)

External Links:

MathReview (Z. Nehari), ZentralBlatt

Referenced by:

§32.7(v).

Encodings:

BibTeX

►

One-parameter systems of solutions of Painlevé equations. Differ. Uravn. 14 (12), pp. 2131–2135 (Russian).

ⓘ

Notes:

In Russian. English translation: Differential Equations 14(12), pp. 1510–1513 (1979)

External Links:

ISSN 0374-0641, MathReview (M. Tvrdý), ZentralBlatt

Referenced by:

§32.10(i), §32.10(ii), §32.10(iii), §32.7(iv).

Encodings:

BibTeX

… ►

Algorithm 300: Coulomb wave functions. Comm. ACM 10 (4), pp. 244–245.

ⓘ

Notes:

For remarks see same journal 12(1969), p. 692 and 16(1973), pp. 308-309 and for certification see same journal 12(1969), pp. 279-280.

External Links:

ISSN 0001-0782, Document

Referenced by:

§33.26(ii).

Encodings:

BibTeX

…

18: 3.4 Differentiation

… ►

3.4.23 $$\frac{{\partial }^2{u}_{0,0}}{{\partial x}^2}=\frac{1}{12h^2}(-u_{2,0}+16u_{1,0}-30u_{0,0}+16u_{-1,0}-u_{-2,0})+O\left(h^4\right),$$

ⓘ

Symbols:

$O\left(x\right)$: order not exceeding, $\frac{\partial f}{\partial x}$: partial derivative of $f$ with respect to $x$ , $\partial x$: partial differential of $x$ and $u$: function

A&S Ref:

25.3.24

Permalink:

http://dlmf.nist.gov/3.4.E23

Encodings:

pMML, png, TeX

See also:

Annotations for §3.4(iii), §3.4(iii), §3.4 and Ch.3

… ►

3.4.29 $${\nabla }^2{u}_{0,0}=\frac{1}{12h^2}\left(-60u_{0,0}+16(u_{1,0}+u_{0,1}+u_{-1,0}+u_{0,-1})-(u_{2,0}+u_{0,2}+u_{-2,0}+u_{0,-2})\right)+O\left(h^4\right).$$

ⓘ

Symbols:

$O\left(x\right)$: order not exceeding and $u$: function

A&S Ref:

25.3.31

Permalink:

http://dlmf.nist.gov/3.4.E29

Encodings:

pMML, png, TeX

See also:

Annotations for §3.4(iii), §3.4(iii), §3.4 and Ch.3

…

19: 1.3 Determinants, Linear Operators, and Spectral Expansions

… ►

1.3.1

ⓘ

Symbols:

$det$: determinant, $j$: integer and $k$: integer

Permalink:

http://dlmf.nist.gov/1.3.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §1.3(i), §1.3(i), §1.3 and Ch.1

… ►Higher-order determinants are natural generalizations. The minor $M_{jk}$ of the entry $a_{jk}$ in the $n$th-order determinant $det[a_{jk}]$ is the ($n-1$)th-order determinant derived from $det[a_{jk}]$ by deleting the $j$th row and the $k$th column. …An $n$th-order determinant expanded by its $j$th row is given by … ►

1.3.8

ⓘ

Symbols:

$det$: determinant

Permalink:

http://dlmf.nist.gov/1.3.E8

Encodings:

pMML, png, TeX

See also:

Annotations for §1.3(i), §1.3(i), §1.3 and Ch.1

…

20: Bibliography D

… ►

Strong asymptotics of orthogonal polynomials with respect to exponential weights. Comm. Pure Appl. Math. 52 (12), pp. 1491–1552.

ⓘ

External Links:

ISSN 0010-3640, Document, MathReview (D. S. Lubinsky), ZentralBlatt

Referenced by:

§18.32.

Encodings:

BibTeX

… ►

Computation of the incomplete gamma function ratios and their inverses. ACM Trans. Math. Software 12 (4), pp. 377–393.

ⓘ

External Links:

ISSN 0098-3500, Document, ZentralBlatt

Referenced by:

§8.12, §8.25(iii).

Encodings:

BibTeX

… ►

A simplified algorithm for the second-order sound fields. J. Acoust. Soc. Amer. 108 (6), pp. 2759–2764.

ⓘ

External Links:

Document

Referenced by:

§8.24(iii).

Encodings:

BibTeX

… ►

Algorithm 322. F-distribution. Comm. ACM 11 (2), pp. 116–117.

ⓘ

Notes:

Includes Algol program, maximum accuracy 10S. For certification see same journal 12(1969), p. 39

External Links:

ISSN 0001-0782, Document

Referenced by:

§8.28(iv).

Encodings:

BibTeX

… ►

Olver’s error bound methods applied to linear ordinary differential equations having a simple turning point. Anal. Appl. (Singap.) 12 (4), pp. 385–402.

ⓘ

External Links:

ISSN 0219-5305, Document, Link, MathReview (Thomas Mbah Acho), ZentralBlatt

Referenced by:

5th item, §14.32.

Encodings:

BibTeX

…