13 Confluent Hypergeometric Functions Kummer Functions 13.6 Relations to Other Functions 13.8 Asymptotic Approximations for Large Parameters

§13.7 Asymptotic Expansions for Large Argument

Keywords:: Kummer functions
Referenced by:: §13.29(i), §13.29(ii)
Permalink:: http://dlmf.nist.gov/13.7

§13.7(i) Poincaré-Type Expansions
§13.7(ii) Error Bounds
§13.7(iii) Exponentially-Improved Expansion

§13.7(i) Poincaré-Type Expansions

Notes:: See Temme (1996b, §7.2) or Olver (1997b, pp. 256–258).
Permalink:: http://dlmf.nist.gov/13.7.i

As $x\to\infty$

13.7.1 $\mathop{{\mathbf{M}}\/}\nolimits\!\left(a,b,x\right)\sim\frac{e^{x}x^{{a-b}}}{% \mathop{\Gamma\/}\nolimits\!\left(a\right)}\sum_{{s=0}}^{{\infty}}\frac{\left(% 1-a\right)_{{s}}\left(b-a\right)_{{s}}}{s!}x^{{-s}},$

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, $\mathop{{\mathbf{M}}\/}\nolimits\!\left(a,b,z\right)$ : Olver’s confluent hypergeometric function, $\left(a\right)_{{n}}$ : Pochhammer’s symbol, : base of exponential function, : : factorial, $\sim$ : asymptotic equality, : nonnegative integer and : real variable
Permalink:: http://dlmf.nist.gov/13.7.E1
Encodings:: TeX, pMML, png

provided that $a\neq 0,-1,\dots$ .

As $z\to\infty$

13.7.2 $\mathop{{\mathbf{M}}\/}\nolimits\!\left(a,b,z\right)\sim\frac{e^{z}z^{{a-b}}}{% \mathop{\Gamma\/}\nolimits\!\left(a\right)}\sum_{{s=0}}^{{\infty}}\frac{\left(% 1-a\right)_{{s}}\left(b-a\right)_{{s}}}{s!}z^{{-s}}+\frac{e^{{\pm\pi ia}}z^{{-% a}}}{\mathop{\Gamma\/}\nolimits\!\left(b-a\right)}\sum_{{s=0}}^{{\infty}}\frac% {\left(a\right)_{{s}}\left(a-b+1\right)_{{s}}}{s!}(-z)^{{-s}},$ $-\frac{1}{2}\pi+\delta\leq\pm\mathop{\mathrm{ph}\/}\nolimits z\leq\frac{3}{2}% \pi-\delta$ ,

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, $\mathop{{\mathbf{M}}\/}\nolimits\!\left(a,b,z\right)$ : Olver’s confluent hypergeometric function, $\left(a\right)_{{n}}$ : Pochhammer’s symbol, : base of exponential function, : : factorial, $\mathop{\mathrm{ph}\/}\nolimits$ : phase, $\sim$ : asymptotic equality, : nonnegative integer, : complex variable and $\delta$ : small positive constant
A&S Ref:: 13.5.1 (with corrected region of validity)
Referenced by:: §13.2(iv), §13.7(ii), §13.9(i)
Permalink:: http://dlmf.nist.gov/13.7.E2
Encodings:: TeX, pMML, png

unless $a=0,-1,\dots$ and $b-a=0,-1,\dots$ . Here $\delta$ denotes an arbitrary small positive constant. Also,

13.7.3 $\mathop{U\/}\nolimits\!\left(a,b,z\right)\sim z^{{-a}}\sum_{{s=0}}^{{\infty}}% \frac{\left(a\right)_{{s}}\left(a-b+1\right)_{{s}}}{s!}(-z)^{{-s}},$ $|\mathop{\mathrm{ph}\/}\nolimits z|\leq\tfrac{3}{2}\pi-\delta$ .

Symbols:: $\mathop{U\/}\nolimits\!\left(a,b,z\right)$ : Kummer confluent hypergeometric function, $\left(a\right)_{{n}}$ : Pochhammer’s symbol, : : factorial, $\mathop{\mathrm{ph}\/}\nolimits$ : phase, $\sim$ : asymptotic equality, : nonnegative integer, : complex variable and $\delta$ : small positive constant
A&S Ref:: 13.5.2
Referenced by:: §12.9(i), §13.12, §13.2(i)
Permalink:: http://dlmf.nist.gov/13.7.E3
Encodings:: TeX, pMML, png

§13.7(ii) Error Bounds

Notes:: See Olver (1965).
Keywords:: Kummer functions
Referenced by:: §12.9(ii), §13.19
Permalink:: http://dlmf.nist.gov/13.7.ii

Figure 13.7.1: Regions ${\textbf{R}}_{1}$ , ${\textbf{R}}_{2}$ , $\overline{\textbf{R}}_{2}$ , ${\textbf{R}}_{3}$ , and $\overline{\textbf{R}}_{3}$ are the closures of the indicated unshaded regions bounded by the straight lines and circular arcs centered at the origin, with

Referenced by:: §13.7(ii)
Permalink:: http://dlmf.nist.gov/13.7.F1
Encodings:: pdf, png

13.7.4 $\mathop{U\/}\nolimits\!\left(a,b,z\right)=z^{{-a}}\sum_{{s=0}}^{{n-1}}\frac{% \left(a\right)_{{s}}\left(a-b+1\right)_{{s}}}{s!}(-z)^{{-s}}+\varepsilon_{{n}}% (z),$

Symbols:: $\mathop{U\/}\nolimits\!\left(a,b,z\right)$ : Kummer confluent hypergeometric function, $\left(a\right)_{{n}}$ : Pochhammer’s symbol, : : factorial, : nonnegative integer, : nonnegative integer, : complex variable and $\varepsilon_{n}(z)$ : function
Referenced by:: §13.2(i), §13.7(ii)
Permalink:: http://dlmf.nist.gov/13.7.E4
Encodings:: TeX, pMML, png

where

13.7.5 $\left|\varepsilon_{{n}}(z)\right|,~{}\beta^{{-1}}\left|\varepsilon_{{n}}^{{% \prime}}(z)\right|\leq 2\alpha C_{n}\left|\frac{\left(a\right)_{{n}}\left(a-b+% 1\right)_{{n}}}{n!z^{{a+n}}}\right|\mathop{\exp\/}\nolimits\!\left(\frac{2% \alpha\rho C_{1}}{|z|}\right),$

Symbols:: $\left(a\right)_{{n}}$ : Pochhammer’s symbol, $\mathop{\exp\/}\nolimits z$ : exponential function, : : factorial, : nonnegative integer, : complex variable, $\varepsilon_{n}(z)$ : function, $C_{n}$ : coefficient, $\alpha$ , $\beta$ and $\rho$
Referenced by:: §13.2(i)
Permalink:: http://dlmf.nist.gov/13.7.E5
Encodings:: TeX, pMML, png

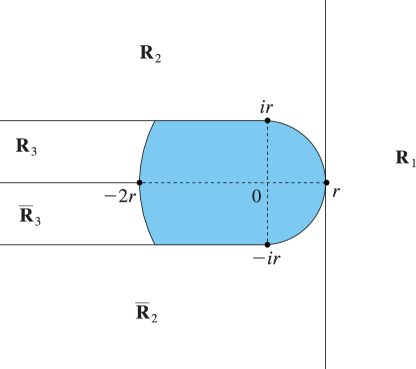
and with the notation of Figure 13.7.1

13.7.6

$C_{n}=1$ ,

$\chi(n)$ ,

$\left(\chi(n)+\sigma\nu^{2}n\right)\nu^{n}$ ,

Symbols:: : nonnegative integer, $C_{n}$ : coefficient, $\sigma$ , $\nu$ and $\chi(n)$ : function
Permalink:: http://dlmf.nist.gov/13.7.E6
Encodings:: TeX, TeX, TeX, pMML, pMML, pMML, png, png, png

according as

13.7.7

$z\in\textbf{R}_{1}$ ,

$z\in\textbf{R}_{2}\cup\overline{\textbf{R}}_{2}$ ,

$z\in\textbf{R}_{3}\cup\overline{\textbf{R}}_{3}$ ,

Symbols:: $\in$ : element of, $\cup$ : union and : complex variable
Permalink:: http://dlmf.nist.gov/13.7.E7
Encodings:: TeX, TeX, TeX, pMML, pMML, pMML, png, png, png

respectively, with

13.7.8

$\sigma=\left|\ifrac{(b-2a)}{z}\right|$ ,

$\nu=\left(\tfrac{1}{2}+\tfrac{1}{2}\sqrt{1-4\sigma^{2}}\right)^{{-\ifrac{1}{2}}}$ ,

$\chi(n)=\sqrt{\pi}\mathop{\Gamma\/}\nolimits\!\left(\tfrac{1}{2}n+1\right)/% \mathop{\Gamma\/}\nolimits\!\left(\tfrac{1}{2}n+\tfrac{1}{2}\right)$ .

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, : nonnegative integer, : complex variable, $\sigma$ , $\nu$ and $\chi(n)$ : function
Permalink:: http://dlmf.nist.gov/13.7.E8
Encodings:: TeX, TeX, TeX, pMML, pMML, pMML, png, png, png

Also, when $z\in\textbf{R}_{1}\cup\textbf{R}_{2}\cup\overline{\textbf{R}}_{2}$

13.7.9

$\alpha=\frac{1}{1-\sigma}$ ,

$\beta=\frac{1-\sigma^{2}+\sigma|z|^{{-1}}}{2(1-\sigma)}$ ,

$\rho=\tfrac{1}{2}\left|2a^{2}-2ab+b\right|+\frac{\sigma(1+\frac{1}{4}\sigma)}{% (1-\sigma)^{2}}$ ,

Symbols:: : complex variable, $\sigma$ , $\alpha$ , $\beta$ and $\rho$
Referenced by:: §13.7(ii), §13.7(ii)
Permalink:: http://dlmf.nist.gov/13.7.E9
Encodings:: TeX, TeX, TeX, pMML, pMML, pMML, png, png, png

and when $z\in\textbf{R}_{3}\cup\overline{\textbf{R}}_{3}$ $\sigma$ is replaced by $\nu\sigma$ and $|z|^{{-1}}$ is replaced by $\nu|z|^{{-1}}$ everywhere in (13.7.9).

For numerical values of $\chi(n)$ see Table 9.7.1.

Corresponding error bounds for (13.7.2) can be constructed by combining (13.2.41) with (13.7.4)–(13.7.9).

§13.7(iii) Exponentially-Improved Expansion

Keywords:: Kummer functions
Referenced by:: §12.9(ii), §13.19
Permalink:: http://dlmf.nist.gov/13.7.iii

Let

13.7.10 $\mathop{U\/}\nolimits\!\left(a,b,z\right)=z^{{-a}}\sum_{{s=0}}^{{n-1}}\frac{% \left(a\right)_{{s}}\left(a-b+1\right)_{{s}}}{s!}(-z)^{{-s}}+R_{{n}}(a,b,z),$

Symbols:: $\mathop{U\/}\nolimits\!\left(a,b,z\right)$ : Kummer confluent hypergeometric function, $\left(a\right)_{{n}}$ : Pochhammer’s symbol, : : factorial, : nonnegative integer, : nonnegative integer, : complex variable and $R_{{n}}(a,b,z)$ : remainder
Referenced by:: §13.29(i)
Permalink:: http://dlmf.nist.gov/13.7.E10
Encodings:: TeX, pMML, png

and

13.7.11 $R_{{n}}(a,b,z)=\frac{(-1)^{{n}}2\pi z^{{a-b}}}{\mathop{\Gamma\/}\nolimits\!% \left(a\right)\mathop{\Gamma\/}\nolimits\!\left(a-b+1\right)}\left(\sum_{{s=0}% }^{{m-1}}\frac{\left(1-a\right)_{{s}}\left(b-a\right)_{{s}}}{s!}(-z)^{{-s}}G_{% {n+2a-b-s}}(z)+\left(1-a\right)_{{m}}\left(b-a\right)_{{m}}R_{{m,n}}(a,b,z)% \right),$

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, $\left(a\right)_{{n}}$ : Pochhammer’s symbol, : : factorial, : integer, : nonnegative integer, : nonnegative integer, : complex variable, $G_{p}(z)$ : expansion and $R_{{n}}(a,b,z)$ : remainder
Referenced by:: §13.29(i)
Permalink:: http://dlmf.nist.gov/13.7.E11
Encodings:: TeX, pMML, png

where is an arbitrary nonnegative integer, and

13.7.12 $G_{{p}}(z)=\frac{e^{z}}{2\pi}\mathop{\Gamma\/}\nolimits\!\left(p\right)\mathop% {\Gamma\/}\nolimits\!\left(1-p,z\right).$

Symbols:: $\mathop{\Gamma\/}\nolimits\!\left(z\right)$ : gamma function, : base of exponential function, $\mathop{\Gamma\/}\nolimits\!\left(a,z\right)$ : incomplete gamma function, : complex variable and $G_{p}(z)$ : expansion
Permalink:: http://dlmf.nist.gov/13.7.E12
Encodings:: TeX, pMML, png

(For the notation see §8.2(i).) Then as $z\to\infty$ with $\left|\left|z\right|-n\right|$ bounded and fixed

13.7.13 $R_{{m,n}}(a,b,z)=\begin{cases}\mathop{O\/}\nolimits\!\left(e^{{-|z|}}z^{{-m}}% \right),&|\mathop{\mathrm{ph}\/}\nolimits z|\leq\pi,\\ \mathop{O\/}\nolimits\!\left(e^{{z}}z^{{-m}}\right),&\pi\leq|\mathop{\mathrm{% ph}\/}\nolimits z|\leq\tfrac{5}{2}\pi-\delta.\\ \end{cases}$

Symbols:: $\mathop{O\/}\nolimits\!\left(x\right)$ : order not exceeding, : base of exponential function, $\mathop{\mathrm{ph}\/}\nolimits$ : phase, : integer, : nonnegative integer, : complex variable, $\delta$ : small positive constant and $R_{{n}}(a,b,z)$ : remainder
Permalink:: http://dlmf.nist.gov/13.7.E13
Encodings:: TeX, pMML, png

For proofs see Olver (1991b, 1993a). For extensions to hyperasymptotic expansions see Olde Daalhuis and Olver (1995a).

© 2010–2013 NIST / Privacy Policy / Disclaimer / Feedback; Version 1.0.6; Release date 2013-05-06 Math-Image version (See MathML) . A Printed Companionis available. 13.6 Relations to Other Functions 13.8 Asymptotic Approximations for Large Parameters

§13.7 Asymptotic Expansions for Large Argument

Contents

§13.7(i) Poincaré-Type Expansions

§13.7(ii) Error Bounds

§13.7(iii) Exponentially-Improved Expansion